Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài tập cuối chương 4 chi tiết sách Toán 12 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài tập cuối chương 4

A. Trắc nghiệm

Bài 4.20 trang 27 Toán 12 Tập 2: Một nguyên hàm của hàm số f(x) = sin2x là:

A. F(x) = 2cos2x.

B. F(x) = −cos2x.

C. $F\left(x\right)=\frac{1}{2}\cos 2x$

D. $F\left(x\right)=\frac{-1}{2}\cos 2x$

Lời giải:

Đáp án đúng là: D

Vì $F^{\text{'}}\left(x\right)={\left(\frac{-1}{2}\cos 2x\right)}^{\text{'}}=\sin 2x$ nên $F\left(x\right)=\frac{-1}{2}\cos 2x$ là một nguyên hàm của hàm số f(x) = sin2x.

Bài 4.21 trang 27 Toán 12 Tập 2: Họ tất cả các nguyên hàm của hàm số 2ex là

A. 2xe^x + C.

B. −2e^x + C.

C. 2e^x.

D. 2e^x + C.

Lời giải:

Đáp án đúng là: D

Có $\int 2e^{x}dx=2\int e^{x}dx=2e^x+C$

Bài 4.22 trang 27 Toán 12 Tập 2: Nguyên hàm F(x) của hàm số f(x) = e^x – 3e^−x thỏa mãn F(0) = 4 là

A. F(x) = e^x – 3e^−x.

B. F(x) = e^x + 3e^−2x.

C. F(x) = e^x + 3e^−x.

D. F(x) = e^x + 3e^−x + 4.

Lời giải:

Đáp án đúng là: C

Ta có $F\left(x\right)=\int \left(e^x-3e^{-x}\right)dx=e^x+3e^{-x}+C$

Vì F(0) = 4 nên e⁰ + 3e⁻⁰ + C = 4 Þ C = 0.

Vậy F(x) = e^x + 3e^−x.

Bài 4.23 trang 27 Toán 12 Tập 2: Cho hàm số f(x) có đạo hàm f'(x) liên tục trên ℝ, f(1) = 16 và $\underset{1}{\overset{3}{\int }}{f}^{\text{'}}\left(x\right)dx=4$. Khi đó giá trị của f(3) bằng

A. 20.

B. 16.

C. 12.

D. 10.

Lời giải:

Đáp án đúng là: A

Có $\underset{1}{\overset{3}{\int }}{f}^{\text{'}}\left(x\right)dx=4$$\iff {\left.f\left(x\right)\right|}_1^3=4$$\iff f\left(3\right)-f\left(1\right)=4\Rightarrow f\left(3\right)=4+f\left(1\right)=4+16=20$

Bài 4.24 trang 27 Toán 12 Tập 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x² – 2x, y = −x² + 4x và hai đường thẳng x = 0, x = 3 là

A. −9.

B. 9.

C. $\frac{16}{3}$

D. $\frac{20}{3}$

Lời giải:

Đáp án đúng là: B

Diện tích cần tìm là:

$S=\underset{0}{\overset{3}{\int }}\left|x^2-2x+x^2-4x\right|dx$$=\underset{0}{\overset{3}{\int }}\left|2x^2-6x\right|dx$$=\underset{0}{\overset{3}{\int }}\left(6x-2x^2\right)dx$

$={\left.\left(3x^2-\frac{2}{3}{x}^3\right)\right|}_0^3$

Bài 4.25 trang 27 Toán 12 Tập 2: Cho đồ thị hàm số y = f(x) trên đoạn [−2;2] như Hình 4.32.

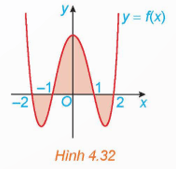
Biết $\underset{-2}{\overset{-1}{\int }}f\left(x\right)dx=\underset{1}{\overset{2}{\int }}f\left(x\right)dx=-\frac{22}{15}$ và $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=\frac{76}{15}$. Khi đó, diện tích của hình phẳng được tô màu là

A. 8.

B. $\frac{22}{15}$

C. $\frac{32}{15}$

D. $\frac{76}{15}$

Lời giải:

Đáp án đúng là: A

Diện tích cần tìm là:

$S=\underset{-2}{\overset{2}{\int }}\left|f\left(x\right)\right|dx$$=\underset{-2}{\overset{-1}{\int }}\left|f\left(x\right)\right|dx+\underset{-1}{\overset{1}{\int }}\left|f\left(x\right)\right|dx+\underset{1}{\overset{2}{\int }}\left|f\left(x\right)\right|dx$

$=-\underset{-2}{\overset{-1}{\int }}f\left(x\right)dx+\underset{-1}{\overset{1}{\int }}f\left(x\right)dx-\underset{1}{\overset{2}{\int }}f\left(x\right)dx$

$=\frac{22}{15}+\frac{76}{15}+\frac{22}{15}=8$

Bài 4.26 trang 28 Toán 12 Tập 2: Cho hình phẳng (S) giới hạn bởi đồ thị hàm số $y=\sqrt{1-x^2}$, trục hoành và hai đường thẳng x = −1, x = 1. Thể tích của khối tròn xoay khi quay (S) quanh trục Ox là

A. $\frac{3\pi }{4}$

B. $\frac{3\pi }{2}$

C. $\frac{2\pi }{3}$

D. $\frac{4\pi }{3}$

Lời giải:

Đáp án đúng là: D

Thể tích cần tìm là:

$V=\pi \underset{-1}{\overset{1}{\int }}\left(1-x^2\right)dx$$=\pi {\left.\left(x-\frac{x^3}{3}\right)\right|}_{-1}^1$$=\pi \left(1-\frac{1}{3}+1-\frac{1}{3}\right)=\frac{4\pi }{3}$

Bài 4.27 trang 28 Toán 12 Tập 2: Một vật chuyển động có gia tốc là a(t) = 3t² + t (m/s²). Biết rằng vận tốc ban đầu của vật là 2 m/s. Vận tốc của vật đó sau 2 giây là

A. 8 m/s.

B. 10 m/s.

C. 12 m/s.

D. 16 m/s.

Lời giải:

Đáp án đúng là: C

Có $v\left(t\right)=\int a\left(t\right)dt=\int \left(3t^2+t\right)dt=t^3+\frac{t^2}{2}+C$

Vì v(0) = 2 nên C = 2.

Do đó $v\left(t\right)=t^3+\frac{t^2}{2}+2$

Vậy $v\left(2\right)=2^3+\frac{2^2}{2}+2=12$ (m/s).

B. Tự luận

Bài 4.28 trang 28 Toán 12 Tập 2: Tìm họ tất cả các nguyên hàm của các hàm số sau:

a) $y=2^x-\frac{1}{x}$

b) $y=x\sqrt{x}+3\cos x-\frac{2}{{\sin }^{2}x}$

Lời giải:

a) $\int \left(2^x-\frac{1}{x}\right)dx=\int 2^{x}dx-\int \frac{1}{x}dx=\frac{2^x}{\ln 2}-\ln \left|x\right|+C$

b) $\int \left(x\sqrt{x}+3\cos x-\frac{2}{{\sin }^{2}x}\right)dx$$=\int x^{\frac{3}{2}}dx+3\int \cos xdx-2\int \frac{1}{{\sin }^{2}x}dx$

$=\frac{2}{5}{x}^{\frac{5}{2}}+3\sin x+2\cot x+C$

Bài 4.29 trang 28 Toán 12 Tập 2: Tìm một nguyên hàm F(x) của hàm số $f\left(x\right)=2\cos x+\frac{1}{{\sin }^{2}x}$ thỏa mãn điều kiện $F\left(\frac{\pi }{4}\right)=-1$.

Lời giải:

Có $F\left(x\right)=\int f\left(x\right)dx=\int \left(2\cos x+\frac{1}{{\sin }^{2}x}\right)dx$$=2\int \cos xdx+\int \frac{1}{{\sin }^{2}x}dx$

$=2\sin x-\cot x+C$

Vì $F\left(\frac{\pi }{4}\right)=-1$ nên $2\sin \frac{\pi }{4}-\cot \frac{\pi }{4}+C=-1$$\Rightarrow C=-\sqrt{2}$

Vậy $F\left(x\right)=2\sin x-\cot x-\sqrt{2}$

Bài 4.30 trang 28 Toán 12 Tập 2: Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với vận tốc ban đầu là 30 m/s. Gia tốc trọng trường là 9,8 m/s². Tìm vận tốc của viên đạn ở thời điểm 2 giây.

Lời giải:

Chọn chiều dương là chiều hướng từ mặt đất lên.

Ta có a = −9,8 m/s². Do đó v(t) = −9,8t + C.

Vì v(0) = 30 nên C = 30. Do đó v(t) = −9,8t + 30.

Vận tốc của viên đạn ở thời điểm 2 giây là: v(2) = −9,8.2 + 30 = 10,4 m/s.

Bài 4.31 trang 28 Toán 12 Tập 2: Cá hồi Thái Bình Dương đến mùa sinh sản thường bơi từ biển ngược dòng vào sông và đến thượng nguồn các dòng sông để đẻ trứng. Giả sử cá bơi ngược dòng sông với vận tốc là $v\left(t\right)=-\frac{2t}{5}+4$(km/h). Nếu coi thời điểm ban đầu t = 0 là lúc cá bắt đầu bơi vào dòng sông thì khoảng cách xa nhất mà con cá có thể bơi được là bao nhiêu?

Lời giải:

Ta có $s\left(t\right)=\int v\left(t\right)dt=\int \left(-\frac{2}{5}t+4\right)dt=-\frac{t^2}{5}+4t+C$

Vì thời điểm ban đầu t = 0 là lúc cá bắt đầu bơi vào dòng sông nên s(0) = 0, suy ra C = 0.

Do đó $s\left(t\right)=-\frac{t^2}{5}+4t$

Ta có $s\left(t\right)=-\frac{1}{5}\left(t^2-20t\right)=-\frac{1}{5}\left(t^2-20t+100\right)+20=-\frac{1}{5}{\left(t-10\right)}^2+20\le \mathrm{20,}\forall t\ge 0$

Vậy khoảng cách xa nhất mà con cá có thể bơi là 20 km.

Bài 4.32 trang 28 Toán 12 Tập 2: Tính các tích phân sau:

a) $\underset{1}{\overset{4}{\int }}\left(x^3-2\sqrt{x}\right)dx$

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(\cos x-\sin x\right)dx$

c) $\underset{\frac{\pi }{6}}{\overset{\frac{\pi }{4}}{\int }}\frac{dx}{{\sin }^{2}x}$

d) $\underset{1}{\overset{16}{\int }}\frac{x-1}{\sqrt{x}}dx$

Lời giải:

a) $\underset{1}{\overset{4}{\int }}\left(x^3-2\sqrt{x}\right)dx$$=\underset{1}{\overset{4}{\int }}{x}^{3}dx-2\underset{1}{\overset{4}{\int }}{x}^{\frac{1}{2}}dx$$={\left.\left(\frac{x^4}{4}-\frac{4}{3}{x}^{\frac{3}{2}}\right)\right|}_1^4$$=\frac{160}{3}+\frac{13}{12}=\frac{653}{12}$

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(\cos x-\sin x\right)dx$$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\cos xdx-\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sin xdx$$={\left.\left(\sin x+\cos x\right)\right|}_0^{\frac{\pi }{2}}=1-1=0$

c) $\underset{\frac{\pi }{6}}{\overset{\frac{\pi }{4}}{\int }}\frac{dx}{{\sin }^{2}x}={\left.-\cot x\right|}_{\frac{\pi }{6}}^{\frac{\pi }{4}}=-1+\sqrt{3}$

d) $\underset{1}{\overset{16}{\int }}\frac{x-1}{\sqrt{x}}dx$$=\underset{1}{\overset{16}{\int }}\sqrt{x}dx-\underset{1}{\overset{16}{\int }}\frac{1}{\sqrt{x}}dx$$=\underset{1}{\overset{16}{\int }}{x}^{\frac{1}{2}}dx-\underset{1}{\overset{16}{\int }}{x}^{-\frac{1}{2}}dx$

$={\left.\left(\frac{2}{3}{x}^{\frac{3}{2}}-2x^{\frac{1}{2}}\right)\right|}_1^{16}$$=\frac{104}{3}+\frac{4}{3}=36$

Bài 4.33 trang 28 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi các đường y = e^x, y = x, x = 0 và x = 1.

Lời giải:

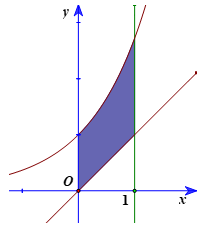
Diện tích cần tính là:

$S=\underset{0}{\overset{1}{\int }}\left|e^x-x\right|dx$$=\underset{0}{\overset{1}{\int }}\left(e^x-x\right)dx$$=\underset{0}{\overset{1}{\int }}{e}^{x}dx-\underset{0}{\overset{1}{\int }}xdx$$={\left.\left(e^x-\frac{x^2}{2}\right)\right|}_0^1=e-\frac{1}{2}-1=e-\frac{3}{2}$

Bài 4.34 trang 28 Toán 12 Tập 2: Tính thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox:

a) y = 1 – x², y = 0, x = −1, x = 1;

b) $y=\sqrt{25-x^2},y=\mathrm{0,}x=\mathrm{2,}x=4$

Lời giải:

a) Thể tích cần tìm là:

$V=\pi \underset{-1}{\overset{1}{\int }}{\left(1-x^2\right)}^{2}dx$$=\pi \underset{-1}{\overset{1}{\int }}\left(1-2x^2+x^4\right)dx$

$={\left.\pi \left(x-\frac{2}{3}{x}^3+\frac{x^5}{5}\right)\right|}_{-1}^1$$=\pi \left(\frac{8}{15}+\frac{8}{15}\right)=\frac{16\pi }{15}$

b) Thể tích cần tìm là:

$V=\pi \underset{2}{\overset{4}{\int }}\left(25-x^2\right)dx$$={\left.\pi \left(25x-\frac{x^3}{3}\right)\right|}_2^4$$=\pi \left(\frac{236}{3}-\frac{142}{3}\right)=\frac{94\pi }{3}$

Bài 4.35 trang 28 Toán 12 Tập 2: Nghệ thuật làm gốm có lịch sử phát triển lâu đời và vẫn còn tồn tại cho đến ngày nay. Giả sử một bình gốm có mặt trong của bình là một mặt tròn xoay sinh ra khi cho phần đồ thị của hàm số $y=\frac{1}{175}{x}^2+\frac{3}{35}x+5\left(0\le x\le 30\right)$ (x, y tính theo cm) quay tròn quanh bệ gốm có trục trùng với trục Ox. Hỏi để hoàn thành bình gốm đó ta cần sử dụng bao nhiêu cm³ đất sét, biết rằng bình gốm đó có độ dày không đổi là 1 cm.

Lời giải:

Thể tích đất sét cần sử dụng là:

$V=\pi \underset{0}{\overset{31}{\int }}{\left(\frac{1}{175}{x}^2+\frac{3}{35}x+5\right)}^{2}dx-\pi \underset{0}{\overset{30}{\int }}{\left(\frac{1}{175}{x}^2+\frac{3}{35}x+5\right)}^{2}dx$

$=\pi \underset{0}{\overset{30}{\int }}{\left(\frac{1}{175}{x}^2+\frac{3}{35}x+5\right)}^{2}dx+\pi \underset{30}{\overset{31}{\int }}{\left(\frac{1}{175}{x}^2+\frac{3}{35}x+5\right)}^{2}dx-\pi \underset{0}{\overset{30}{\int }}{\left(\frac{1}{175}{x}^2+\frac{3}{35}x+5\right)}^{2}dx$

$=\pi \underset{30}{\overset{31}{\int }}{\left(\frac{1}{175}{x}^2+\frac{3}{35}x+5\right)}^{2}dx$

$=\pi \underset{30}{\overset{31}{\int }}\left(\frac{1}{{175}^2}{x}^4+\frac{9}{1225}{x}^2+25+\frac{6}{6125}{x}^3+\frac{2}{35}{x}^2+\frac{6}{7}x\right)dx$

$=\pi \underset{30}{\overset{31}{\int }}\left(\frac{1}{{175}^2}{x}^4+\frac{6}{6125}{x}^3+\frac{79}{1225}{x}^2+\frac{6}{7}x+25\right)dx$

$=\pi {\left.\left(\frac{x^5}{153125}+\frac{3x^4}{12250}+\frac{79x^3}{3675}+\frac{3x^2}{7}+25x\right)\right|}_{30}^{31}$

$\approx \pi \left(\mathrm{2240,4}-\mathrm{2073,2}\right)=\mathrm{167,2}\pi$ (cm³).

Vậy để hoàn thành bình gốm đó ta cần sử dụng 167,2π cm³ đất sét.

Xem thêm các bài giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài 13. Ứng dụng hình học của tích phân

Bài tập cuối chương 4

Bài 14. Phương trình mặt phẳng

Bài 15. Phương trình đường thẳng trong không gian

Bài 16. Công thức tính góc trong không gian

Bài 17. Phương trình mặt cầu