Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số chi tiết sách Toán 12 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:
Giải bài tập Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Sơ đồ khảo sát hàm số
HĐ1 trang 26 Toán 12 Tập 1: Cho hàm số . Thực hiện lần lượt các yêu cầu sau:
a) Tính y’ và tìm các điểm tại đó .
b) Xét dấu y’ để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.
c) Tính , và lập bảng biến thiên của hàm số.
d) Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.
Lời giải:
a) Tập xác định:
Ta có:
Vậy với thì .
b) Trên khoảng , nên hàm số nghịch biến. Trên khoảng , nên hàm số đồng biến.
Hàm số đạt cực tiểu tại giá trị cực tiểu . Hàm số không có cực đại.
c)
Bảng biến thiên:
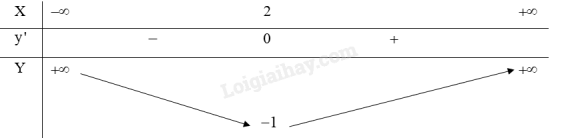
d) Đồ thị:
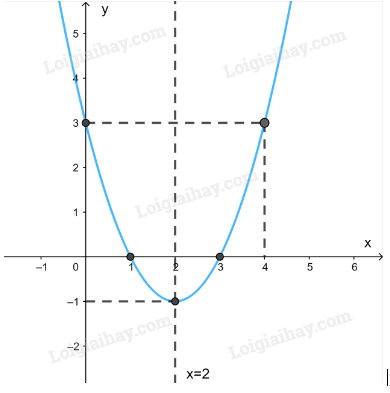
Giao điểm của đồ thị hàm số với trục tung là .
Ta có: . Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm .
Điểm thuộc đồ thị hàm số .
Đồ thị hàm số nhận đường thẳng làm trục đối xứng.
d) Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là .
Ta có: . Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm .
Điểm thuộc đồ thị hàm số .
Đồ thị hàm số nhận đường thẳng làm trục đối xứng.
2. Khảo sát và vẽ đồ thị hàm số đa thức bậc 3
Luyện tập 1 trang 28 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số .
Lời giải:
1. Tập xác định:
2. Sự biến thiên:
Ta có: với mọi
Hàm số nghịch biến trên .
Hàm số không có cực trị.
Giới hạn tại vô cực:
Bảng biến thiên:
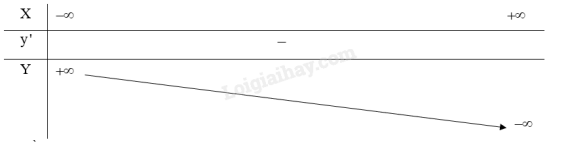
3. Đồ thị:
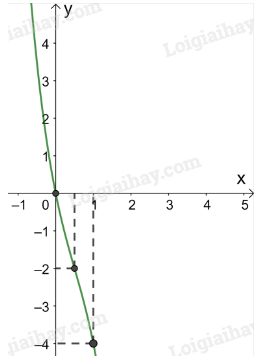
Giao điểm của đồ thị hàm số với trục tung là .
Ta có: . Do đó, giao điểm của đồ thị hàm số với trục hoành là điểm (0; 0).
Điểm thuộc đồ thị hàm số .
Đồ thị hàm số có tâm đối xứng là điểm .
3. Khảo sát và vẽ đồ thị hàm số phân thức hữu tỉ
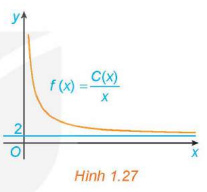
Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là . Hãy giải thích tại sao chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/ sản phẩm. Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình 1.27 như thế nào?
Lời giải:
Ta có:
Vì với mọi nên hàm số là hàm số giảm.
Do đó, chi phí trung bình giảm theo x nhưng luôn lớn 2 triệu đồng/ sản phẩm.
Điều này được thể hiện trong Hình 1.27 là đồ thị hàm số có tiệm cận ngang là đường thẳng và đi xuống trong khoảng .
a) Tính thể tích nước và khối lượng chất khử trùng có trong bể sau t phút. Từ đó tính nồng độ chất khử trùng (gam/lít) trong bể sau t phút.
b) Coi nồng độ chất khử trùng là hàm số f(t) với . Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Hãy giải thích tại sao nồng độ chất khử tăng theo t nhưng không vượt ngưỡng 0,5 gam/lít.
Lời giải:
a) Thể tích nước trong bể sau t phút là: (l).
Khối lượng chất khử trùng trong bể sau t phút là: (g).
Nồng độ chất khử trùng trong bể sau t phút là: (gam/lít).
b) Hàm số về nồng độ chất khử trùng là:
Khảo sát và vẽ đồ thị hàm số .
1. Tập xác định của hàm số:
2. Sự biến thiên:
Ta có: với mọi .
Hàm số đồng biến trên khoảng .
Hàm số không có cực trị.
Tiệm cận:
Do đó, đồ thị hàm số nhận đường thẳng làm tiệm cận ngang (phần bên phải trục Oy).
Bảng biến thiên:
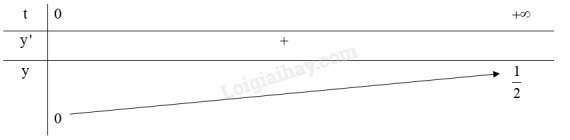
3. Đồ thị:
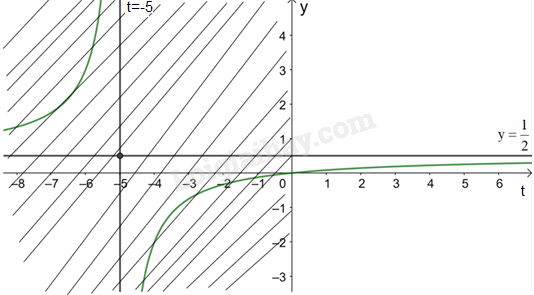
Giao điểm của đồ thị hàm số với trục tung là .
Giao điểm của đồ thị hàm số với trục hoành là điểm (0; 0).
Đồ thị hàm số là phần màu xanh không bị gạch chéo.
c) Vì với mọi và nên nồng độ chất khử trùng tăng theo t nhưng không vượt ngưỡng 0,5 gam/ lít.
Luyện tập 3 trang 32 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số .
Lời giải:
1. Tập xác định của hàm số:
2. Sự biến thiên:
Ta có:
Hàm số nghịch biến trên khoảng và .
Hàm số không có cực trị.
Do đó, đồ thị hàm số nhận đường thẳng làm tiệm cận đứng và đường thẳng làm tiệm cận xiên.
Bảng biến thiên:

3. Đồ thị:
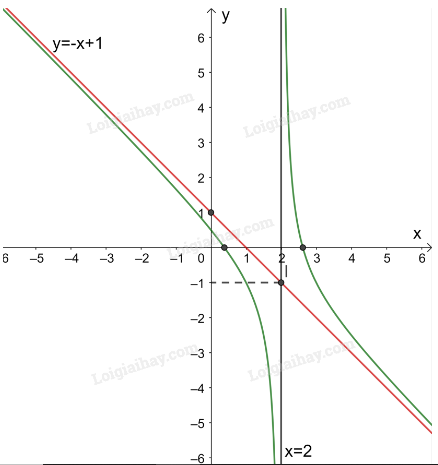
Giao điểm của đồ thị hàm số với trục tung là .
hoặc
Giao điểm của đồ thị hàm số với trục hoành là các điểm.
Đồ thị hàm số nhận giao điểm của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
Bài tập
Bài 1.21 trang 32 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) ;
b) .
Lời giải:
a) Tập xác định:
2. Sự biến thiên:
Ta có:
Trên khoảng , nên hàm số đồng biến. Trên khoảng và , nên hàm số nghịch biến trên mỗi khoảng đó.
Hàm số đạt cực đại tại , giá trị cực đại . Hàm số đạt cực tiểu tại , giá trị cực tiểu
Giới hạn tại vô cực:
Bảng biến thiên:
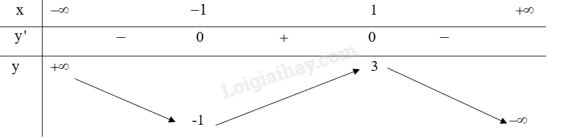
3. Đồ thị:
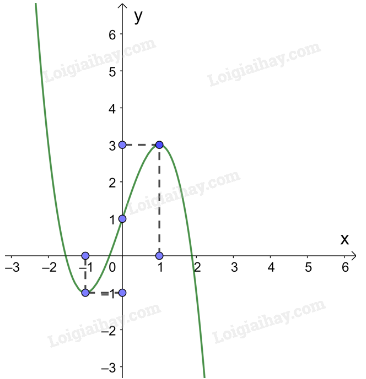
Giao điểm của đồ thị hàm số với trục tung là (0; 1).
Các điểm (1; 3); thuộc đồ thị hàm số .
Đồ thị hàm số có tâm đối xứng là điểm (0; 1).
b) 1. Tập xác định:
2. Sự biến thiên:
Ta có: hoặc
Trên khoảng , nên hàm số nghịch biến. Trên khoảng và , nên hàm số đồng biến trên mỗi khoảng đó.
Hàm số đạt cực đại tại , giá trị cực đại . Hàm số đạt cực tiểu tại , giá trị cực tiểu .
Giới hạn tại vô cực:
Bảng biến thiên:

3. Đồ thị:
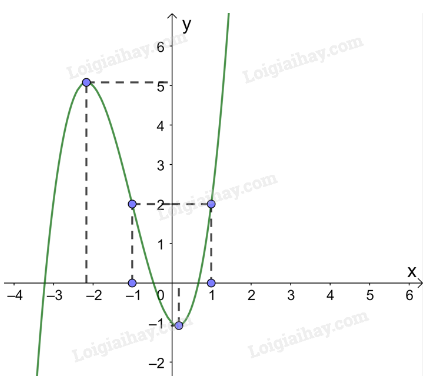
Giao điểm của đồ thị hàm số với trục tung là (0; -1).
Các điểm (-1; 2); thuộc đồ thị hàm số .
Đồ thị hàm số có tâm đối xứng là điểm (-1; 2).
Bài 1.22 trang 32 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) ;
b) .
Lời giải:
a) 1. Tập xác định của hàm số:
2. Sự biến thiên:
Hàm số đồng biến trên khoảng và .
Hàm số không có cực trị.
.
.
Do đó, đồ thị hàm số nhận đường thẳng làm tiệm cận đứng và đường thẳng làm tiệm cận ngang.
Bảng biến thiên:

3. Đồ thị: Giao điểm của đồ thị hàm số với trục tung là (0;1).
Giao điểm của đồ thị hàm số với trục hoành là điểm .
Đồ thị hàm số nhận giao điểm I(-1; 2) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
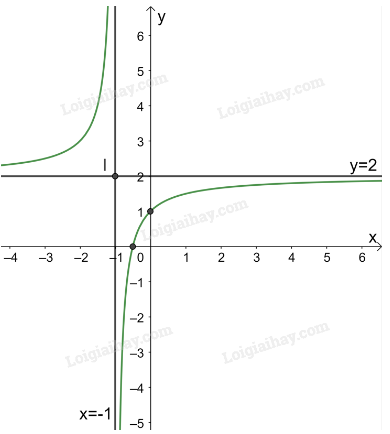
b) 1. Tập xác định của hàm số:
2. Sự biến thiên:
Hàm số đồng biến trên khoảng và .
Hàm số không có cực trị.
Do đó, đồ thị hàm số nhận đường thẳng làm tiệm cận đứng và đường thẳng làm tiệm cận ngang.
Bảng biến thiên:

3. Đồ thị:
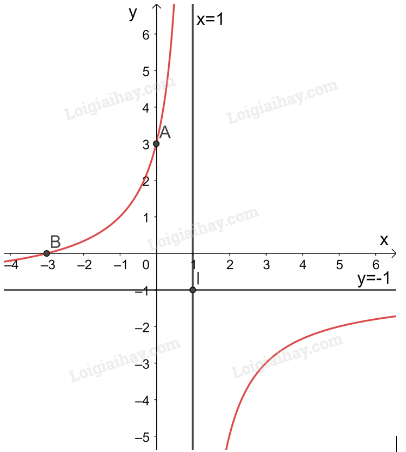
Giao điểm của đồ thị hàm số với trục tung là (0; 3).
Giao điểm của đồ thị hàm số với trục hoành là điểm .
Đồ thị hàm số nhận giao điểm I(1; -1) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
a) ;
b) .
Lời giải:
a) 1. Tập xác định của hàm số:
2. Sự biến thiên:
Ta có:
hoặc
Trong khoảng và , nên hàm số đồng biến.
Trong khoảng và , nên hàm số nghịch biến.
Hàm số đạt cực đại tại , giá trị cực đại .
Hàm số đạt cực tiểu tại , giá trị cực đại .
Do đó, đồ thị hàm số nhận đường thẳng làm tiệm cận đứng và đường thẳng làm tiệm cận xiên.
Bảng biến thiên:
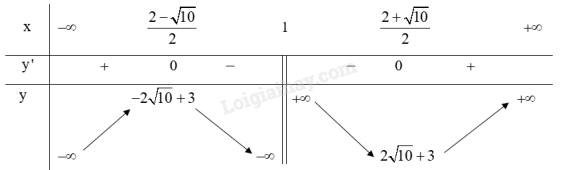
3. Đồ thị:
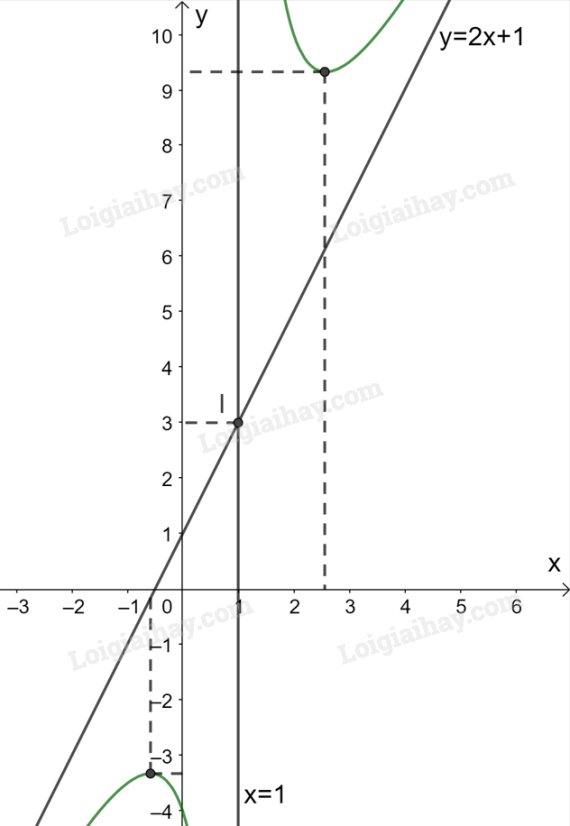
Giao điểm của đồ thị hàm số với trục tung là (0; -4).
Đồ thị hàm số không cắt trục Ox.
Đồ thị hàm số nhận giao điểm I(1; 3) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
b)
1. Tập xác định của hàm số:
2. Sự biến thiên:
Ta có:
hoặc .
Trong khoảng và , nên hàm số đồng biến.
Trong khoảng và , nên hàm số nghịch biến.
Hàm số đạt cực đại tại , giá trị cực đại .
Hàm số đạt cực tiểu tại , giá trị cực tiểu .
Do đó, đồ thị hàm số nhận đường thẳng làm tiệm cận đứng và đường thẳng làm tiệm cận xiên.
Bảng biến thiên:
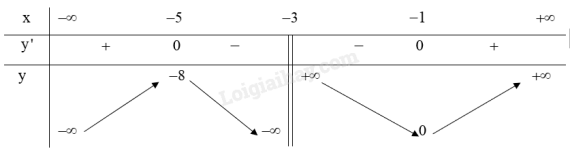
3. Đồ thị:
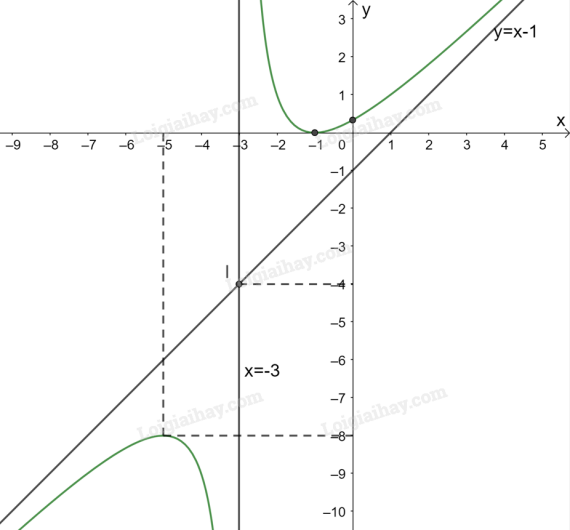
Giao điểmcủa đồ thị hàm số với trục tung là .
Giao điểm của đồ thị hàm số với trục hoành là điểm .
Đồ thị hàm số nhận giao điểm của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x).
b) Coi hàm C(x) là hàm số xác định với . Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml.
Lời giải:
a) Khối lượng dung dịch trong cốc sau khi trộn x(ml) KOH từ bình chứa là:
Thể tích dung dịch trong cốc sau khi trộn x(ml) KOH từ bình chứa là:
Nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa là:
b) Khảo sát hàm số với .
1. Tập xác định của hàm số:
2. Sự biến thiên:
Hàm số nghịch biến trên .
Hàm số không có cực trị.
.
Do đó, đồ thị hàm số nhận đường thẳng làm tiệm cận ngang (phần bên phải trục Oy)
Bảng biến thiên:

3. Đồ thị: Giao điểm của đồ thị hàm số với trục tung là (0;100).
Đồ thị hàm số đi qua các điểm (200; 20); .
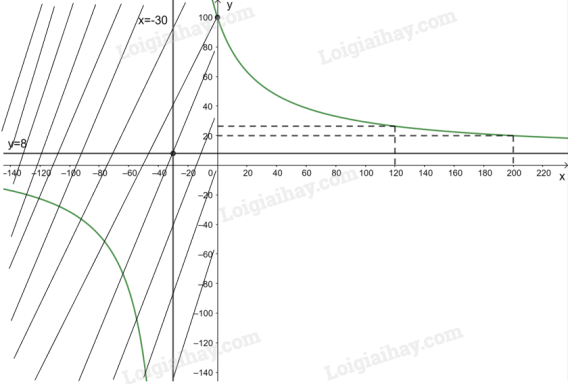
Đồ thị của hàm số với là phần nét màu xanh không bị gạch chéo.
c) Vì và nên nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml
Giả sử một điện trở được mắc song song với một biến trở như Hình 1.33. Nếu điện trở đó được kí hiệu là thì điện trở tương đương R là hàm số của x. Vẽ đồ thị của hàm số và dựa vào đồ thị đã vẽ, hãy cho biết:
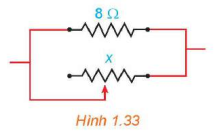
a) Điện trở tương đương của mạch thay đổi thế nào khi x tăng.
b) Tại sao điện trở tương đương của mạch không bao giờ vượt quá .
Lời giải:
Khi một điện trở được mắc song song với một biến trở thì điện trở tương đương của mạch là:
Vẽ đồ thị hàm số với .
1. Tập xác định của hàm số:
2. Sự biến thiên:
Hàm số đồng trên .
Hàm số không có cực trị.
.
Do đó, đồ thị hàm số với nhận đường thẳng làm tiệm cận ngang (phần bên phải trục Oy).
Bảng biến thiên:
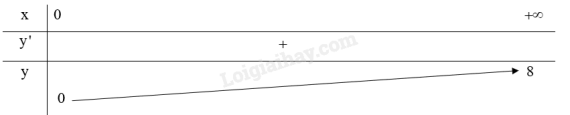
3. Đồ thị:
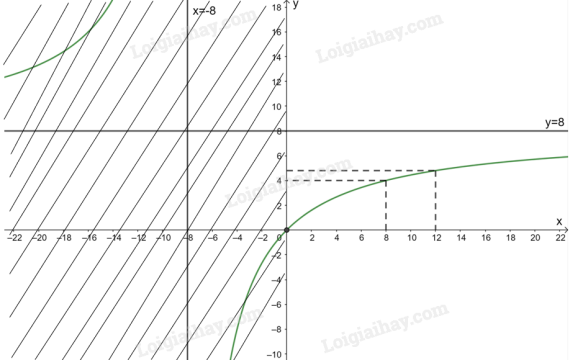
Giao điểm của đồ thị hàm số với trục tung là (0; 0).
Đồ thị hàm số đi qua các điểm (8; 4); .
a) Vì nên khi x tăng thì điện trở tương đương của mạch tăng.
b) Vì và nên điện trở tương đương của mạch không bao giờ vượt quá .
Xem thêm các bài giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:
Bài 3. Đường tiệm cận của đồ thị hàm số
Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
Bài 7. Hệ trục toạ độ trong không gian
Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Sơ đồ khảo sát hàm số
Các bước khảo sát hàm số
|
1. Tìm tập xác định của hàm số 2. Khảo sát sự biến thiên của hàm số - Tính đạo hàm y’. Tìm các điểm tại đó y’ = 0 hoặc đạo hàm không tồn tại - Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số - Tìm cực trị của hàm số - Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số (nếu có) - Lập BBT của hàm số 3. Vẽ đồ thị của hàm số dựa vào BBT |
2. Khảo sát và vẽ đồ thị hàm số đa thức bậc ba
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Tập xác định của hàm số: R
2. Sự biến thiên:
- Ta có: . Vậy y’ = 0 khi x = 0 hoặc x = 2
- Trên khoảng , y’ > 0 nên hàm số đồng biến. Trên các khoảng và , y’ < 0 nên hàm số nghịch biến trên mỗi khoảng đó
- Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu . Hàm số đạt cực đại tại x = 2, giá trị cực đại
- Giới hạn tại vô cực:
- BBT:
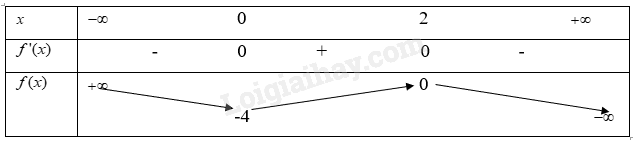
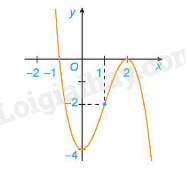
3. Đồ thị:
- Giao điểm của đồ thị hàm số với trục tung là điểm
- Ta có: y = 0 x = -1 hoặc x = 2. Do đó giao điểm của đồ thị hàm số với trục hoành là các điểm và
- Đồ thị hàm số có tâm đối xứng là điểm
3. Khảo sát và vẽ đồ thị hàm số phân thức hữu tỷ
a) Hàm số phân thức
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên:
- Ta có: với mọi
- Hàm số nghịch biến trên từng khoảng và
- Hàm số không có cực trị
- Tiệm cận:
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận ngang là y = 1
- BBT:
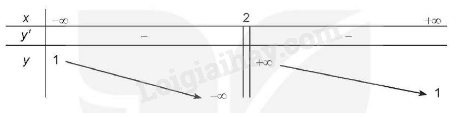
3. Đồ thị:
- Giao điểm của đồ thị hàm số với trục tung là điểm
- Giao điểm của đồ thị hàm số với trục hoành là điểm
- Đồ thị hàm số nhận giao điểm I của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng
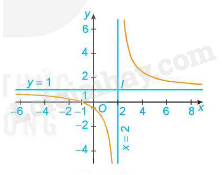
b) Hàm số phân thức (đa thức tử không chia hết cho đa thức mẫu)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên: Viết
- Ta có: . Vậy y’ = 0 x = 1 hoặc x = 3
- Trên các khoảng và , y’ > 0 nên hàm số đồng biến trên từng khoảng này
- Trên các khoảng và , y’ < 0 nên hàm số nghịch biến trên từng khoảng này
- Hàm số đạt cực đại tại x = 1 với ; hàm số đạt cực tiểu tại x = 3 với
;
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận xiên là y = x+1
- BBT:
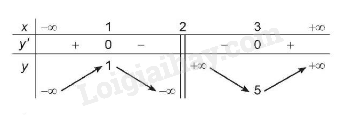
3. Đồ thị:
- Giao điểm của đồ thị hàm số với trục tung là điểm
- Ta có: . Do đó giao điểm của đồ thị hàm số với trục hoành là điểm
- Đồ thị hàm số nhận giao điểm I của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng