Với giải Luyện tập 3 trang 32 Toán 12 Tập 1 Kết nối tri thức chi tiết trong Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Luyện tập 3 trang 32 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y=\frac{-x^2+3x-1}{x-2}$.

Lời giải:

1. Tập xác định của hàm số: $\mathbb{R}\mathrm{\setminus }\left\{2\right\}$

2. Sự biến thiên:

Ta có: $y=\frac{-x^2+3x-1}{x-2}=-x+1+\frac{1}{x-2}$

$y^{\prime }=-1-\frac{1}{{\left(x-2\right)}^2}<0\mathrm{\forall }x\ne 2$

Hàm số nghịch biến trên khoảng $\left(-\mathrm{\infty };2\right)$ và $\left(2;+\mathrm{\infty }\right)$.

Hàm số không có cực trị.

$\underset{x\to +\mathrm{\infty }}{lim}y=\underset{x\to +\mathrm{\infty }}{lim}\frac{-x^2+3x-1}{x-2}=-\mathrm{\infty };\underset{x\to -\mathrm{\infty }}{lim}y=\underset{x\to -\mathrm{\infty }}{lim}\frac{-x^2+3x-1}{x-2}=+\mathrm{\infty }$
$\underset{x\to 2^{-}}{lim}y=\underset{x\to 2^{-}}{lim}\frac{-x^2+3x-1}{x-2}=-\mathrm{\infty };\underset{x\to 2^{+}}{lim}y=\underset{x\to 2^{+}}{lim}\frac{-x^2+3x-1}{x-2}=+\mathrm{\infty }$

$\underset{x\to +\mathrm{\infty }}{lim}\left[y-\left(-x+1\right)\right]=\underset{x\to +\mathrm{\infty }}{lim}\left(-x+1+\frac{1}{x-2}+x-1\right)=\underset{x\to +\mathrm{\infty }}{lim}\frac{1}{x-2}=0$

$\underset{x\to -\mathrm{\infty }}{lim}\left[y-\left(-x+1\right)\right]=\underset{x\to -\mathrm{\infty }}{lim}\left(-x+1+\frac{1}{x-2}+x-1\right)=\underset{x\to -\mathrm{\infty }}{lim}\frac{1}{x-2}=0$

Do đó, đồ thị hàm số nhận đường thẳng $x=2$ làm tiệm cận đứng và đường thẳng $y=-x+1$ làm tiệm cận xiên.

Bảng biến thiên:

3. Đồ thị:

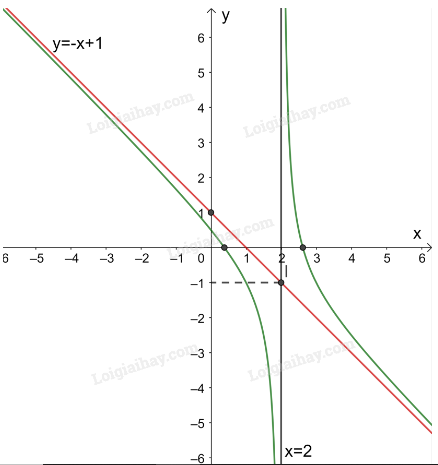
Giao điểm của đồ thị hàm số với trục tung là $\left(0;\frac{1}{2}\right)$.

$y=0\iff \frac{-x^2+3x-1}{x-2}=0\iff x=\frac{3+\sqrt{5}}{2}$ hoặc $x=\frac{3-\sqrt{5}}{2}$

Giao điểm của đồ thị hàm số với trục hoành là các điểm$\left(\frac{3+\sqrt{5}}{2};0\right);\left(\frac{3-\sqrt{5}}{2};0\right)$.

Đồ thị hàm số nhận giao điểm $I\left(2;-1\right)$ của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.