Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau chi tiết sách Toán 7 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau

1. Tỉ lệ thức

Giải Toán 7 trang 6 Tập 2

Khám phá 1 trang 6 Toán lớp 7: Cho hai máy tính xách tay (laptop) có kích thước màn hình (tính theo đơn vị mm) lần lượt là 227,6 × 324 và 170,7 × 243. Tính tỉ số giữa chiều rộng và chiều dài của mỗi màn hình.

Phương pháp giải:

Thực hiện lập các tỉ số giữa chiều dài và chiều rộng màn hình mỗi máy tính theo dạng phân số

Lời giải:

Xét tỉ số giữa chiều dài và chiều rộng của máy tính thứ nhất là : ${\displaystyle \frac{227,6}{324}}$

Tỉ số giữa chiều dài và chiều rộng của máy tính thứ hai là : ${\displaystyle \frac{170,7}{243}}$

Thực hành 1 trang 6 Toán lớp 7: a) Từ các tỉ số ${\displaystyle \frac{6}{5}}:2$ và ${\displaystyle \frac{12}{5}}:4$ có lập được một tỉ lệ thức hay không?

b) Hãy lập hai tỉ lệ thức từ bốn số 9;2;3;6.

Phương pháp giải:

a)      Thực hiện các phép tính để tối giản thành 2 tỉ số và xem có thể lập tỉ lệ thức được không

b)      Lập các tỉ số từ các số đã cho sao cho 2 tỉ số bằng nhau sẽ có thể lập được các tỉ lệ thức .

Lời giải:

a)      Ta xét tỉ số ${\displaystyle \frac{6}{5}}:2={\displaystyle \frac{6}{5}}.{\displaystyle \frac{1}{2}}={\displaystyle \frac{6}{10}}={\displaystyle \frac{3}{5}}$

Tương tự xét với tỉ số ${\displaystyle \frac{12}{5}}:4={\displaystyle \frac{12}{5}}.{\displaystyle \frac{1}{4}}={\displaystyle \frac{12}{20}}={\displaystyle \frac{12:4}{20:4}}={\displaystyle \frac{3}{5}}$

Ta thấy các tỉ số đều bằng ${\displaystyle \frac{3}{5}}$ nên ta sẽ lập được một tỉ lệ thức : ${\displaystyle \frac{12}{5}}:4$ = ${\displaystyle \frac{6}{5}}:2$

b)      Từ các số 9;2;3;6 ta thấy :

${\displaystyle \frac{9}{3}}$= 3 và ${\displaystyle \frac{6}{2}}$=3 nên suy ra ta có tỉ lệ thức thứ nhất : ${\displaystyle \frac{9}{3}}$=${\displaystyle \frac{6}{2}}$

Ta xét tỉ số ${\displaystyle \frac{9}{6}}$=${\displaystyle \frac{9:3}{6:3}}$=${\displaystyle \frac{3}{2}}$nên ta có được tỉ lệ thức thứ hai : ${\displaystyle \frac{9}{6}}$=${\displaystyle \frac{3}{2}}$

Vận dụng 1 trang 6 Toán lớp 7: Chứng minh các tỉ số giữa chiều rộng và chiều dài của màn hình hai loại máy tính đã nêu trong HĐ 1 sẽ tạo thành 1 tỉ lệ thức.

Phương pháp giải:

So sánh tỉ số giữa chiều dài và chiều rộng của màn hình 2 loại máy tính nếu các tỉ số đó bằng nhau ta sẽ được một tỉ lệ thức .

Lời giải:

Xét tỉ số giữa chiều dài và chiều rộng của máy tính thứ nhất là : ${\displaystyle \frac{227,6}{324}}$

Tỉ số giữa chiều dài và chiều rộng của máy tính thứ hai là : ${\displaystyle \frac{170,7}{243}}$

Để 2 tỉ số bằng nhau $\iff$ ${\displaystyle \frac{227,6}{324}}$-${\displaystyle \frac{170,7}{243}}$= 0

Ta thấy ước chung lớn nhất của 324 và 243 là 81 nên ta sẽ chia cả tử và mẫu của 2 phân số để mẫu số chung là 81

$\begin{array}{l}\Rightarrow {\displaystyle \frac{227,6:4}{324:4}}-{\displaystyle \frac{170,7:3}{243:3}}=0\\ \iff {\displaystyle \frac{56,9}{81}}-{\displaystyle \frac{56,9}{81}}=0\end{array}$

Ta thấy 2 tỉ số bằng nhau vì sau khi rút gọn và trừ đi được kết quả là 0

$\Rightarrow$ 2 tỉ số chiều dài và chiều rộng màn hình của mỗi loại máy tính là bằng nhau nên sẽ tạo thành một tỉ lệ thức .

Khám phá 2 trang 6 Toán lớp 7: a) Từ tỉ lệ thức ${\displaystyle \frac{48}{64}}={\displaystyle \frac{9}{12}}$, ta nhân cả hai vế với 64.12 thì có kết quả gì?

b) Từ tỉ lệ thức ${\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}}$, ta nhân cả hai vế với b.d thì có kết quả gì?

Phương pháp giải:

a)      Nhân hai vế với 64.12

b)      Từ câu a ta rút ra mối quan hệ khi nhân 2 vế với b.d

Lời giải:

a)      ${\displaystyle \frac{48}{64}}={\displaystyle \frac{9}{12}}$ta nhân cả 2 vế cho 64.12 được : ${\displaystyle \frac{48}{64}}.(64.12)={\displaystyle \frac{9}{12}}.(64.12)$

$\Rightarrow$${\displaystyle \frac{\mathrm{48.64.12}}{64}}={\displaystyle \frac{\mathrm{9.64.12}}{12}}$$\Rightarrow$$48.12$= $9.64$ $\iff$ 576 = 48.12 = 9.64

$\Rightarrow$ Ta thấy nhân cả 2 vế với 64.12 ta được 2 vế sau khi rút gọn bằng nhau

b)      ${\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}}$ nhân cả 2 vế với b.d ta có : ${\displaystyle \frac{a\cdot b\cdot d}{b}}={\displaystyle \frac{c\cdot b.d}{d}}$ sau khi rút gọn cả 2 vế ta được : a.b = c.d

Giải Toán 7 trang 7 Tập 2

Khám phá 3 trang 7 Toán lớp 7: Từ đẳng thức 48.12 = 64.9, ta chia cả hai vế cho 64.12 thì có kết quả gì?

Từ đẳng thức ad = cb, ta chia cả hai vế cho bd thì có kết quả gì?

Phương pháp giải:

• Thực hiện nhân chia 2 vế cho 64.12 và rút gọn kết quả cuối cùng của 2 vế
• So sánh 2 vế từ đó rút ra được kết quả của đẳng thức ab = cd

Lời giải:

• Ta nhân rồi chi cả 2 vế cho 64.12

48 . 12 = 576 ta lấy 576 : (64 . 12) = ${\displaystyle \frac{576}{768}}$ ta thấy ước chung lớn nhất của tử và mẫu là 192 nên ta rút gọn phân số ${\displaystyle \frac{576:192}{768:192}}={\displaystyle \frac{3}{4}}$

Xét vế trái 64 . 9 = 576 ta lấy 567 : (64 . 12) = ${\displaystyle \frac{576}{768}}={\displaystyle \frac{3}{4}}$

Như vậy sau khi chia cả 2 vế cho 64 . 12 ta được kết quả là cả 2 vế bằng nhau và cùng bằng ${\displaystyle \frac{3}{4}}$

• Từ đẳng thức ad = cb ta chia cả 2 vế cho bd sẽ được ${\displaystyle \frac{ad}{bd}}={\displaystyle \frac{bc}{bd}}\iff {\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}}$

Thực hành 2 trang 7 Toán lớp 7: Tìm x trong tỉ lệ thức 

Phương pháp giải:

• Sử dụng tính chất thì ad = bc

Lời giải:

Ta có : 

 x = 15

Vậy x = 15

Vận dụng 2 trang 7 Toán lớp 7: Hãy viết một tỉ lệ thức từ đẳng thức x = 2y.

Phương pháp giải:

• Sử dụng tính chất ${\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}}$thì ad = bc

Lời giải:

Ta có đẳng thức : x = 2y

$\Rightarrow$1 . x = 2y

$\Rightarrow$${\displaystyle \frac{2}{x}}={\displaystyle \frac{1}{y}}$ hoặc ${\displaystyle \frac{1}{2}}={\displaystyle \frac{y}{x}}$ hoặc ${\displaystyle \frac{2}{1}}={\displaystyle \frac{x}{y}}$$\iff$$2={\displaystyle \frac{x}{y}}$ hoặc ${\displaystyle \frac{x}{2}}={\displaystyle \frac{1}{y}}$

Vậy từ đẳng thức : x = 2y ta sẽ viết được 4 tỉ lệ thức .

2. Dãy tỉ số bằng nhau

Khám phá 4 trang 7 Toán lớp 7: Các bạn Bình, Mai và Lan cùng thi giải nhanh các bài toán trong sách Bài tập Toán 7. Trong một giờ, số bài làm được của mỗi bạn lần lượt là 4;3;5. Cô giáo thưởng cho mỗi bạn số hình dán lần lượt là 8;6;10. Hãy so sánh tỉ số giữa số hình dán được thưởng và số bài toán làm được của mỗi bạn

Phương pháp giải:

• Xác định số bài làm và số hình dán được thưởng của mỗi bạn là bao nhiêu
• Tính tỉ số giữa số bài tập và số hình dán của mỗi bạn
• So sánh tỉ số giữa hình dán và bài tập làm được của mỗi bạn

Lời giải:

Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Bình là : ${\displaystyle \frac{3}{6}}={\displaystyle \frac{1}{2}}$

Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Mai là : ${\displaystyle \frac{3}{6}}={\displaystyle \frac{1}{2}}$

Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Lan là : ${\displaystyle \frac{5}{10}}={\displaystyle \frac{1}{2}}$

Sau khi rút gọn ta thấy tỉ số giữa số bài làm được và hình dán được thưởng của mỗi bạn đều bằng nhau và cùng bằng ${\displaystyle \frac{1}{2}}$

Thực hành 3 trang 7 Toán lớp 7: Cho biết ba số a,b,c tỉ lệ với các số 2;4;6. Hãy ghi dãy tỉ số bằng nhau tương ứng

Phương pháp giải:

• Lập các phân số là những tỉ số tương ứng
• Lập dãy tỉ số bằng nhau từ những tỉ số đã lập được

Lời giải:

Theo đề bài các số a, b, c tỉ lệ với các số 2, 4, 6

$\Rightarrow$ a : b : c = 2 : 4 : 6

$\Rightarrow$ ${\displaystyle \frac{a}{2}}={\displaystyle \frac{b}{4}}={\displaystyle \frac{c}{6}}$ ( Áp dụng lí thuyết về dãy tỉ số bằng nhau )

Vận dụng 3 trang 7 Toán lớp 7: Gọi m,n,p,q là số quyển vở được chia của bốn bạn Mai, Ngọc, Phú, Quang. Cho biết số điểm 10 đạt được của bốn bạn lần lượt là 12;13;14;15 và số quyển vở được chia tỉ lệ với số điểm 10. Hãy viết dãy tỉ số bằng nhau tương ứng.

Phương pháp giải:

• Lập các tỉ số giữa số quyển vở và số điểm 10 của mỗi bạn tương ứng
• Lập dãy tỉ số bằng nhau từ các tỉ số vừa lập được

Lời giải:

Tỉ số giữa số quyển vở và số điểm 10 của bạn Mai là : ${\displaystyle \frac{m}{12}}$

Tỉ số giữa số quyển vở và số điểm 10 của bạn Ngọc là : ${\displaystyle \frac{n}{13}}$

Tỉ số giữa số quyển vở và số điểm 10 của bạn Phú là : ${\displaystyle \frac{p}{14}}$

Tỉ số giữa số quyển vở và số điểm 10 của bạn Quang là : ${\displaystyle \frac{q}{15}}$

Từ các tỉ số trên ta lập được dãy tỉ số bằng nhau : ${\displaystyle \frac{m}{12}}={\displaystyle \frac{n}{13}}={\displaystyle \frac{p}{14}}={\displaystyle \frac{q}{15}}$

Giải Toán 7 trang 8 Tập 2

Khám phá 5 trang 8 Toán lớp 7: Cho tỉ lệ thức ${\displaystyle \frac{3}{7}}={\displaystyle \frac{9}{21}}$. Hãy tính các tỉ số ${\displaystyle \frac{3+9}{7+21}}$ và ${\displaystyle \frac{3-9}{7-21}}$ rồi so sánh chúng với các tỉ số trong tỉ lệ thức đã cho.

Phương pháp giải:

• Lần lượt thực hiện và tối giản các phép tính
• Từ kết quả thu được và so sánh chúng với các tỉ số trong tỉ lệ đã cho

Lời giải:

Ta có tỉ thức : ${\displaystyle \frac{3}{7}}={\displaystyle \frac{9}{21}}$

Xét ${\displaystyle \frac{3+9}{7+21}}$ = ${\displaystyle \frac{12}{28}}$ = $={\displaystyle \frac{3}{7}}$( chia cả tử và mẫu cho 4 )

Xét ${\displaystyle \frac{3-9}{7-21}}$ = ${\displaystyle \frac{-6}{-14}}$$={\displaystyle \frac{3}{7}}$( chia cả tử và mẫu cho 2 )

Sau khi thực hiện tính các tỉ số ta thấy các kết quả sau khi tối giản của tỉ số bằng với các tỉ só trong tỉ lệ thức đã cho.

Giải Toán 7 trang 9 Tập 2

Thực hành 4 trang 9 Toán lớp 7: Tìm hai số x, y biết rằng:

a)      x + y = 30 và ${\displaystyle \frac{x}{2}}$= ${\displaystyle \frac{y}{3}}$

b)      x – y = −21 và ${\displaystyle \frac{x}{5}}$= ${\displaystyle \frac{y}{-2}}$

Phương pháp giải:

• Áp dụng tính chất ${\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}}={\displaystyle \frac{a\pm c}{b\pm d}}$

Lời giải:

a)      $x+y=30;{\displaystyle \frac{x}{2}}={\displaystyle \frac{y}{3}}$ áp dụng tính chất của tỉ lệ thức ra có :

$\Rightarrow {\displaystyle \frac{x+y}{2+3}}={\displaystyle \frac{x}{2}}$

$\Rightarrow {\displaystyle \frac{30}{5}}={\displaystyle \frac{x}{2}}$

$\Rightarrow 30.2=x.5$

$\begin{array}{l}\Rightarrow 60:5=x\\ \Rightarrow x=12\\ \Rightarrow 14+y=30\\ \Rightarrow y=18\end{array}$    ( thay x vừa tìm được = 12 vào x + y = 30 để tìm ra y )

Vậy x = 12 y = 18

b)      Ta có : ${\displaystyle \frac{x}{5}}={\displaystyle \frac{y}{-2}}$= ${\displaystyle \frac{x-y}{5+2}}$( áp dụng tính chất tỉ lệ thức ) (1)

Mà theo đề bài x – y = -21

Thay -21 vào (1) ta có : ${\displaystyle \frac{-21}{7}}=-3$ $={\displaystyle \frac{x}{5}}$

$\Rightarrow$x = (-3).5

$\Rightarrow$x = -15

Thay x bằng -15 ta có -15 – y = -21

$\Rightarrow$y = -15 + 21

$\Rightarrow$y = 6

Vậy x = -15 và y = 6

Vận dụng 4 trang 9 Toán lớp 7: a) Nguyên liệu của món mứt dừa sau khi hoàn thành chỉ gồm dừa và đường theo tỷ lệ 2 : 1. Tính xem trong 6 kg mứt dừa có bao nhiêu ki-lô-gam dừa và bao nhiêu ki-lô-gam đường.

 b) Bạn Dũng và bạn Thủy muốn làm mứt gừng theo công thức: Cứ 3 phần gừng thì cần 2 phần đường. Hai bạn mua 600g gừng.  Hai bạn cần mua bao nhiêu gam đường?

  c) Mẹ chỉ có 10 quyển vở, số vở chia cho hai chị em An và Bình. Tính số sách chia cho mỗi em, biết rằng số tuổi của An và Bình là 8; 12 và số sách tỉ lệ thuận với số tuổi

Phương pháp giải:

a)      Theo tỉ lệ 2:1 thì trong 6kg mứt dừa sẽ có 3 phần nguyên liệu bằng nhau trong đó 2 phần là dừa còn lại là đường .

b)      Từ số phần gừng và đường ta suy ra được tỉ lệ của gừng và đường . Sau đó lấy tỉ lệ nhân với số gừng đã mua để ra só đường cần mua .

c)      Tính tỉ lệ quyển vở của 2 chị em và vì An nhỏ tuổi hơn nên tỉ lệ của An thấp hơn. Sau đó rút gọn tỉ lệ để tìm được số vở của mỗi người dựa vào số vở đã cho có ở đầu bài.

Lời giải:

a)      Tỉ lệ dừa và đường là : ${\displaystyle \frac{2}{1}}$

Ta có sơ đồ sau :

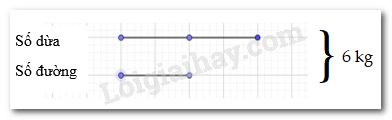
$\Rightarrow$ Số kg đường là : 6 : ( 2+1) = 2 (kg) ( Áp dụng bài toán tổng tỉ đã học ở tiểu học )

$\Rightarrow$ Số kg dừa là : 2 . 2 = 4 (kg)

b)      Tỉ lệ của gừng và đường là 3:2 ta có được tỉ số giữa gừng và đường là  ${\displaystyle \frac{3}{2}}$ nên số đường bằng ${\displaystyle \frac{2}{3}}$ số gừng.

Theo đề bài hai bạn đã mua 600 g gừng nên

$\Rightarrow$ Số đường cần mua là : ${\displaystyle \frac{2}{3}}\times 600$= 400 g

Vậy 2 bạn cần mua 400g đường

c)      Ta có số tuổi của An và Bình lần lượt là 8;12 nên ta sẽ có tỉ số tuổi của 2 bạn là  ${\displaystyle \frac{8}{12}}={\displaystyle \frac{2}{3}}$

Vậy số sách của An và Bình sẽ có tỉ số là 2:3

Theo đề bài chị Chi có 10 quyển vở mà theo tỉ số vừa tính được trong số 10 quyển vở đó An có 2 phần và Bình có 3 phần .

$\Rightarrow$ Số vở của An là 10 : ( 2+3) . 2 = 4 quyển vở ( Áp dụng bài toán tổng tỉ đã được học ở lớp dưới )

$\Rightarrow$ Số vở của Bình là : 10 – 4 = 6 quyển vở .

Thực hành 5 trang 9 Toán lớp 7: Tìm ba số x, y, z, biết x + y + z = 100 và x : y : z = 2 : 3 : 5

Phương pháp giải:

• Từ những tỉ số đề bài cho ta lập được các dãy tỉ số bằng nhau từ tính chất dãy tỉ số bằng nhau .
• Sau khi lập được dãy tỉ số bằng nhau thì thay số lần lượt vào các tỉ số để tìm được x, y, z .

Lời giải:

Từ dãy x : y : z = 2 : 3 : 5 ta có : ${\displaystyle \frac{x}{2}}={\displaystyle \frac{y}{3}}={\displaystyle \frac{z}{5}}$

Mà theo đề bài x + y + z = 100

Áp dụng tính chất dãy tỉ số bằng nhau, ta được:

${\displaystyle \frac{x}{2}}={\displaystyle \frac{y}{3}}={\displaystyle \frac{z}{5}}={\displaystyle \frac{x+y+z}{2+3+5}}={\displaystyle \frac{100}{10}}=10$

$\Rightarrow$ 10 $={\displaystyle \frac{x}{2}}$$\Rightarrow$ x = 10.2 = 20  

$\Rightarrow$ 10 $={\displaystyle \frac{y}{3}}$ $\Rightarrow$ y = 10.3 = 30

$\Rightarrow$ 10 $={\displaystyle \frac{z}{5}}$ $\Rightarrow$ z = 10.5 = 50   

Vận dụng 5 trang 9 Toán lớp 7: Hãy giải bài toán tiền lãi ở hoạt động khởi động (trang 6)

Đầu năm, các bác Xuân, Yến, Dũng góp vốn làm ăn với số tiền lần lượt là 300 triệu đồng, 400 triệu đồng và 500 triệu đồng . Tiền lãi thu được sau một năm là 240 triệu đồng . Hãy tìm số tiền lãi mỗi bác được chia, biết rằng tiền lãi được chia tỉ lệ với số tiền đã góp .

Phương pháp giải:

• Tìm tỉ lệ số vốn mỗi người góp ban đầu .
• Dựa vào tỉ lệ số vốn mỗi người góp ban đầu sẽ tương ứng với tỉ lệ lãi của mỗi người .

Lời giải:

Tổng số vốn của 3 bác Xuân, Yến, Dũng là : 300 + 400 + 500 = 1200 triệu đồng .

Tỉ lệ vốn của bác Xuân là : ${\displaystyle \frac{300}{1200}}$$={\displaystyle \frac{1}{4}}$

TỈ lệ góp vốn của bác Yến là : ${\displaystyle \frac{400}{1200}}$$={\displaystyle \frac{1}{3}}$

Tỉ lệ góp vốn của bác Dũng là  : ${\displaystyle \frac{500}{1200}}$ $={\displaystyle \frac{5}{12}}$

Từ các tỉ lệ góp vốn trên ta tính được tỉ lệ lãi của mỗi người theo số vốn là :

Bác Xuân có số lãi là : ${\displaystyle \frac{1}{4}}\times 240$= 60 ( triệu đồng )

Bác Yến có số lãi là : ${\displaystyle \frac{1}{3}}\times 240$= 80 ( triệu đồng )

Bác Dũng có số lãi là : 240 – 80 -  60 = 100 ( triệu đồng )

Bài tập (trang 10)

Giải Toán 7 trang 10 Tập 2

Bài 1 trang 10 Toán lớp 7: Tìm các tỉ số bằng nhau trong các tỉ số sau đây rồi lập tỉ lệ thức:

$7:21$; ${\displaystyle \frac{1}{5}}:{\displaystyle \frac{1}{2}}$; ${\displaystyle \frac{1}{4}}:{\displaystyle \frac{3}{4}}$; $1,1:3,2;1:2,5$

Lời giải:

 $7:21={\displaystyle \frac{7}{21}}={\displaystyle \frac{1}{3}}$;

${\displaystyle \frac{1}{5}}:{\displaystyle \frac{1}{2}}={\displaystyle \frac{1}{5}}.{\displaystyle \frac{2}{1}}={\displaystyle \frac{2}{5}}$;

${\displaystyle \frac{1}{4}}:{\displaystyle \frac{3}{4}}={\displaystyle \frac{1}{4}}.{\displaystyle \frac{4}{3}}={\displaystyle \frac{1}{3}}$;

$1,1:3,2={\displaystyle \frac{1,1}{3,2}}={\displaystyle \frac{11}{32}}$;

 $1:2,5={\displaystyle \frac{1}{2,5}}={\displaystyle \frac{10}{25}}={\displaystyle \frac{2}{5}}$.

Ta thấy có các tỉ số bằng nhau là :

+) ${\displaystyle \frac{1}{4}}:{\displaystyle \frac{3}{4}}$ và $7:21$ (vì cùng bằng ${\displaystyle \frac{1}{3}}$) nên ta có tỉ lệ thức : ${\displaystyle \frac{1}{4}}:{\displaystyle \frac{3}{4}}=7:21$

+ ${\displaystyle \frac{1}{5}}:{\displaystyle \frac{1}{2}}$ và $1:2,5$ ${\displaystyle \frac{2}{5}}$ (vì cùng bằng ${\displaystyle \frac{2}{5}}$) nên ta có tỉ lệ thức : ${\displaystyle \frac{1}{5}}:{\displaystyle \frac{1}{2}}=1:2,5$

Bài 2 trang 10 Toán lớp 7: Lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:

a) 3 . (-20) = (-4) . 15                                    b) 0,8 . 8,4 = 1,4 . 4,8

Lời giải:

a)      3 . (-20) = (-4) . 15

Áp dụng tính chất của tỉ lệ thức ta có các tỉ lệ thức sau :

${\displaystyle \frac{3}{-4}}={\displaystyle \frac{15}{-20}}$;${\displaystyle \frac{-4}{3}}={\displaystyle \frac{-20}{15}}$;${\displaystyle \frac{3}{15}}={\displaystyle \frac{-4}{-20}}$;${\displaystyle \frac{15}{3}}={\displaystyle \frac{-20}{-4}}$

b)      0,8 . 8,4 = 1,4 . 4,8

Áp dụng tính chất của tỉ lệ thức ta có các tỉ lệ thức sau :

${\displaystyle \frac{0,8}{1,4}}={\displaystyle \frac{4.8}{8.4}}$;${\displaystyle \frac{8,4}{1,4}}={\displaystyle \frac{4.8}{0,8}}$;${\displaystyle \frac{0,8}{4,8}}={\displaystyle \frac{1,4}{8,4}}$;${\displaystyle \frac{8,4}{4,8}}={\displaystyle \frac{1,4}{0,8}}$

Bài 3 trang 10 Toán lớp 7: Tìm hai số x,y biết rằng:

a) ${\displaystyle \frac{x}{4}}={\displaystyle \frac{y}{7}}$ và x + y = 55

b) ${\displaystyle \frac{x}{8}}={\displaystyle \frac{y}{3}}$ và x – y = 35

Lời giải:

a)      Ta có ${\displaystyle \frac{x}{4}}={\displaystyle \frac{y}{7}}$ và x + y = 55

Áp dụng tính chất tỉ lệ thức ta có : ${\displaystyle \frac{x}{4}}={\displaystyle \frac{y}{7}}={\displaystyle \frac{x+y}{4+7}}={\displaystyle \frac{55}{11}}=5$

$\Rightarrow {\displaystyle \frac{x}{4}}=5\Rightarrow x=20$

${\displaystyle \frac{y}{7}}=5\Rightarrow y=35$

Vậy x = 20; y = 35

b)      ${\displaystyle \frac{x}{8}}={\displaystyle \frac{y}{3}}$ và x – y = 35

Áp dụng tính chất tỉ lệ thức ta có : ${\displaystyle \frac{x}{8}}={\displaystyle \frac{y}{3}}={\displaystyle \frac{x-y}{8-3}}={\displaystyle \frac{35}{5}}=7$

$\Rightarrow {\displaystyle \frac{x}{8}}=7$ $\Rightarrow$ x = 56

Mà x – y = 35 $\Rightarrow$ y = 56 – 35 = 21

Vậy x = 56 ; y = 21

Bài 4 trang 10 Toán lớp 7: a) Tìm hai số a,b biết rằng 2a = 5b và 3a + 4b = 46

b) Tìm hai số a,b,c biết rằng a : b : c = 2 : 4 : 5 và a + b – c = 3

Lời giải:

a)      Từ đẳng thức $2a=5b\Rightarrow a=5b:2={\displaystyle \frac{5b}{2}}$

$\Rightarrow 3a={\displaystyle \frac{5b}{2}}.3={\displaystyle \frac{15b}{2}}$

Thay $3a={\displaystyle \frac{15b}{2}}$ vào 3a + 4b = 46, ta được:

$\Rightarrow$${\displaystyle \frac{15b}{2}}+4b=46$

$\Rightarrow$${\displaystyle \frac{15b+8b}{2}}=46$

$\Rightarrow$ 23b = 92

$\Rightarrow$ b = 92 : 23 = 4

Vì b = 4 $\Rightarrow$ 2a = 5.4 $\Rightarrow$ a = 10

Vậy a = 10 ; b = 4

b)      Từ đẳng thức: a : b : c = 2 : 4 : 5 ta có :

$\Rightarrow {\displaystyle \frac{a}{2}}={\displaystyle \frac{b}{4}}={\displaystyle \frac{c}{5}}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\Rightarrow {\displaystyle \frac{a}{2}}={\displaystyle \frac{b}{4}}={\displaystyle \frac{c}{5}}={\displaystyle \frac{a+b-c}{2+4-5}}={\displaystyle \frac{3}{1}}=3$

$\Rightarrow {\displaystyle \frac{a}{2}}={\displaystyle \frac{b}{4}}={\displaystyle \frac{c}{5}}=3$

$\Rightarrow$ $a=6;b=12;c=15$

Bài 5 trang 10 Toán lớp 7: Tính diện tích của hình chữ nhật có chu vi là 28cm và độ dài hai cạnh tỉ lệ với các số 3; 4.

Lời giải:

Nửa chu vi hình chữ nhật là : 28 : 2 = 14 (cm)

Theo đề bài tỉ lệ 2 cạnh với các số 3;4 và vì chiều dài lớn hơn chiều rộng nên ta có

Tỉ số giữa chiều dài và chiều rộng là : ${\displaystyle \frac{3}{4}}$

$\Rightarrow$ Chiều dài của hình chữ nhật là : 14 : ( 3 + 4 ) . 4 = 8 ( cm) ( bài toán tổng tỉ )

$\Rightarrow$ Chiều rộng của hình chữ nhật là : 14 – 8 = 6 (cm)

Bài 6 trang 10 Toán lớp 7: Tại một xí nghiệp may, trong một giờ cả ba tổ A, B, C làm được tổng cộng 60 sản phẩm. Cho biết số sản phẩm làm được của ba tổ A, B, C tỉ lệ với các số 3; 4; 5. Hỏi mỗi tổ làm được bao nhiêu sản phẩm trong một giờ?

Lời giải:

Gọi số sản phẩm tổ A,B,C làm được trong 1 giờ lần lượt là A,B,C ( sản phẩm) (A,B,C > 0)

Theo đề bài cả 3 A,B,C làm trong 1 giờ được 60 sản phẩm ta có :

$\Rightarrow$ A + B + C = 60

Mà 3 tổ A,B,C làm tỉ lệ với các số 3;4;5 nên ta có tỉ lệ thức : ${\displaystyle \frac{A}{3}}={\displaystyle \frac{B}{4}}={\displaystyle \frac{C}{5}}$

Theo tính chất của dãy tỉ số bằng nhau, ta có ${\displaystyle \frac{A}{3}}={\displaystyle \frac{B}{4}}={\displaystyle \frac{C}{5}}$= ${\displaystyle \frac{A+B+C}{3+4+5}}$= ${\displaystyle \frac{60}{12}}=5$

$\Rightarrow$ A = 15 ; B = 20 ; C = 25

Vậy 3 tổ A,B,C lần lượt làm được 15,20,25 sản phẩm trong 1 giờ .

Bài 7 trang 10 Toán lớp 7: Một công ty có ba chi nhánh A, B, C. Kết quả kinh doanh trong tháng vừa qua ở các chi nhánh A và B có lãi còn chi nhánh C lỗ. Cho biết số tiền lãi, lỗ của ba chi nhánh A, B, C tỉ lệ với các số 3; 4; 2. Tìm số tiền lãi, lỗ của mỗi chi nhánh trong tháng vừa qua, biết rằng trong tháng đó công ty lãi được 500 triệu đồng.

Lời giải:

Gọi số tiền chi nhánh A,B lãi, chi nhánh C lỗ lần lượt là A,B,C ( triệu đồng) (A,B,C > 0)

Theo đề bài công ty có 3 chi nhánh A,B,C có số tiền tổng lãi là 500 triệu đồng

Số tiền lãi và lỗ của 3 chi nhánh A,B,C tỉ lệ lần lượt là 3;4;2 trong đó chi nhánh C lỗ

$\Rightarrow$ A + B – C = 500 ( triệu đồng )

Áp dụng tính chất dãy tỉ số bằng nhau, ta có : ${\displaystyle \frac{A}{3}}={\displaystyle \frac{B}{4}}={\displaystyle \frac{C}{2}}$

$\Rightarrow {\displaystyle \frac{A+B-C}{3+4-2}}={\displaystyle \frac{A}{3}}={\displaystyle \frac{B}{4}}={\displaystyle \frac{C}{2}}$

$\Rightarrow {\displaystyle \frac{A+B-C}{3+4-2}}={\displaystyle \frac{A}{3}}={\displaystyle \frac{B}{4}}={\displaystyle \frac{C}{2}}$$={\displaystyle \frac{500}{5}}=100$

$\Rightarrow$A = 300 ; B = 400 ; C = 200

Vậy chi nhánh A lãi 300 triệu đồng, chi nhánh B lãi 400 triệu đồng và chi nhánh C lỗ 200 triệu đồng .

Bài 8 trang 10 Toán lớp 7: Chứng minh rằng từ tỉ lệ thức ${\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}}$ ta suy ra được các tỉ lệ thức sau:

a) ${\displaystyle \frac{a+b}{b}}={\displaystyle \frac{c+d}{d}}$

b) ${\displaystyle \frac{a-b}{b}}={\displaystyle \frac{c-d}{d}}$

c) ${\displaystyle \frac{a}{a+b}}={\displaystyle \frac{c}{c+d}}$ (các mẫu số phải khác 0)

Lời giải:

a) Vì ${\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}}$ nên $ad=bc$

Ta có ${\displaystyle \frac{a+b}{b}}={\displaystyle \frac{c+d}{d}}$$\Rightarrow d(a+b)=b(c+d)$$\Rightarrow ad+bd=bc+bd$

$\Rightarrow ad=bc$ (luôn đúng)

$\Rightarrow {\displaystyle \frac{a+b}{b}}={\displaystyle \frac{c+d}{d}}$ 

b) Vì ${\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}}$ nên $ad=bc$

Ta có: ${\displaystyle \frac{a-b}{b}}={\displaystyle \frac{c-d}{d}}$

$\begin{array}{l}\Rightarrow d(a-b)=b(c-d)\\ \iff ad-bd=bc-bd\\ \iff ad=bc\end{array}$ ( luôn đúng)

Vậy ${\displaystyle \frac{a-b}{b}}={\displaystyle \frac{c-d}{d}}$ 

c)  Vì ${\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}}$ nên $ad=bc$

Ta có: ${\displaystyle \frac{a}{a+b}}={\displaystyle \frac{c}{c+d}}$

$\begin{array}{l}\Rightarrow a(c+d)=c(a+b)\\ \iff ac+ad=ac+bc\\ \iff ad=bc\end{array}$ (luôn đúng)

Vậy ( điều phải chứng minh )

Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:

Bài tập cuối chương 5

Bài 2: Đại lượng tỉ lệ thuận

Bài 3: Đại lượng tỉ lệ nghịch

Bài tập cuối chương 6

Lý thuyết Tỉ lệ thức - Dãy tỉ số bằng nhau

1. Tỉ lệ thức:

1.1. Khái niệm:

Với b, c ≠ 0 ta có tỉ lệ thức là đẳng thức của hai tỉ số: $\frac{a}{b}=\frac{c}{d}$

Tỉ lệ thức còn được viết là: a : b = c : d

Ví dụ:

$\frac{14}{7}=\frac{2}{1}$; $\frac{a}{0,2}=\frac{b}{2}$ là các tỉ lệ thức.

Hoặc có thể viết là: 14 : 7 = 2 : 1; a : 0,2 = b : 2.

1.2. Các tính chất:

* Tính chất 1: Nếu $\frac{a}{b}=\frac{c}{d}$ thì ad = bc. (b.d ≠ 0)

Ví dụ: Nếu ta có tỉ lệ thức $\frac{c}{2}=\frac{d}{3}$ thì 3.c = 2.d.

* Tính chất 2: Ngược lại so với tính chất 1 ta có:

Nếu ad = bc và a, b, c, d ≠ 0 thì ta có những tỉ lệ thức sau:

$\frac{a}{b}=\frac{c}{d}$; $\frac{a}{c}=\frac{b}{d}$; $\frac{d}{c}=\frac{b}{d}$ ; $\frac{d}{b}=\frac{c}{a}$ .

Ví dụ:Cho đẳng thức x.2 = 3.y.Với x, y ≠ 0 ta có các tỉ lệ thức sau:

$\frac{x}{3}=\frac{y}{2}$; $\frac{2}{3}=\frac{y}{x}$ ; $\frac{x}{y}=\frac{3}{2}$ ; $\frac{2}{y}=\frac{3}{x}$ .

2. Dãy tỉ số bằng nhau:

2.1. Khái niệm:

- Ta gọi các đẳng thức: $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}$ là một dãy các tỉ số bằng nhau.

- Khi có dãy tỉ số bằng nhau $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}$ , ta nói các số a, c, e tỉ lệ với các số b, d, f và có thể ghi là: a : c : e = b : d : f.

Ví dụ: Nếu ta có dãy tỉ số bằng nhau $\frac{a}{6}=\frac{b}{7}=\frac{c}{9}$ .

Ta nói các số a, b, c tỉ lệ với các số 6; 7; 9 và có thể ghi là: a : b : c = 6 : 7 : 8.

2.2. Các tính chất:

* Tính chất 1: $\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}=\frac{a-c}{b-d}$(các mẫu số phải khác 0).

Ví dụ:Nếu có tỉ lệ thức: $\frac{5,1}{3}=\frac{1,7}{1}$ .

Khi đó, ta có: $\frac{5,1}{3}=\frac{1,7}{1}=\frac{5,1-1,7}{3-1}=\frac{5,1+1,7}{3+1}$ .

* Tính chất 2: Tương tự với tỉ lệ thức, ta có tính chất sau của dãy tỉ số bằng nhau.

Từ dãy tỉ số bằng nhau $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}$ ta viết được:

$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{a+c+e}{b+d+f}=\frac{a-c+e}{b-d+f}$ (các mẫu số phải khác 0).

Ví dụ:Cho dãy tỉ số bằng nhau: $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$ .

Khi đó, ta có: $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=\frac{x+y+z}{1+2+3}=\frac{x-y+z}{1-2+3}$ .