Giải SGK Toán 7 Bài 27 (Kết nối tri thức): Phép nhân đa thức một biến

Đỗ Thị Ngọc Ánh Ngày: 22-09-2024 Lớp 7

11 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 27: Phép nhân đa thức một biến chi tiết sách Toán 7 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 27: Phép nhân đa thức một biến

Giải Toán 7 trang 36 Tập 2

1. Nhân đơn thức với đa thức

HĐ 1 trang 36 Toán lớp 7: Hãy nhắc lại cách nhân hai đơn thức và tính (12x³).(-5x²)

Phương pháp giải:

Muốn nhân 2 đơn thức, ta nhân hai hệ số với nhau và nhân hai lũy thừa của biến với nhau

Lời giải:

+ Cách nhân 2 đơn thức: Muốn nhân 2 đơn thức, ta nhân hai hệ số với nhau và nhân hai lũy thừa của biến với nhau.

+ Ta có: (12x³).(-5x²) = 12. (-5). (x³ . x²) = -60 . x⁵

HĐ 2 trang 36 Toán lớp 7: Áp dụng tính chất phân phối của phép nhân đối với phép cộng, hãy tìm tích 2x.(3x² – 8x + 1) bằng cách nhân 2x với từng hạng tử của đa thức 3x² – 8x +1 rồi cộng các tích tìm được

Phương pháp giải:

+ Bước 1: Tìm các hạng tử của đa thức 3x² – 8x +1

+ Bước 2 : Nhân 2x với từng hạng tử trên

+ Bước 3: Cộng các tích vừa tìm được

Chú ý: a.(b+c+d) = a.b + a.c + a.d

Lời giải:

Đa thức 3x² – 8x +1 có các hạng tử là: 3x² ; -8x ; 1

Ta có: 2x . 3x² = (2.3). (x.x²) = 6x³

2x. (-8x) = [2.(-8) ]. (x.x) = -16x²

2x.1 = 2x

Vậy 2x.(3x² – 8x + 1) = 6x³ -16x² + 2x

Luyện tập 1 trang 36 Toán lớp 7: Tính: (-2x²) . (3x – 4x³ + 7 – x²)

Phương pháp giải:

+ Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.

Lời giải:

Ta có: (-2x²) . (3x – 4x³ + 7 – x²)

= (-2x²) . 3x + (-2x²) . (-4x³) + (-2x²) . 7 + (-2x²) . (-x²)

= [(-2).3] . (x² . x) + [(-2).(-4)] . (x³ . x²) + [(-2).7] . x² + [(-2).(-1)] . (x² . x²)

= -6x³ + 8x⁵ + (-14)x² + 2x⁴

= 8x⁵ +2x⁴ -6x³ – 14x²

Giải Toán 7 trang 37 Tập 2

Vận dụng 1 trang 37 Toán lớp 7: a) Rút gọn biểu thức P(x) = 7x² . (x² – 5x + 2 ) – 5x .(x³ – 7x² + 3x).

b) Tính giá trị biểu thức P(x) khi x = $- \frac{1}{2}$

Phương pháp giải:

a) Bước 1: Nhân đơn thức với đa thức: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.

Bước 2: Trừ 2 đa thức thu được

b) Thay x = $- \frac{1}{2}$ vào P(x)

Lời giải:

a) P(x) = 7x² . (x² – 5x + 2 ) – 5x .(x³ – 7x² + 3x)

= 7x² . x² + 7x² . (-5x) + 7x² . 2 – [5x. x³ + 5x . (-7x²) + 5x . 3x]

= 7. (x² . x²) + [7.(-5)] . (x² . x) + (7.2).x – {5. (x.x³) + [5.(-7)]. (x.x²) + (5.3).(x.x)}

= 7x⁴ + (-35). x³ + 14x – [ 5x⁴ + (-35)x³ + 15x² ]

= 7x⁴ + (-35). x³ + 14x - 5x⁴ + 35x³ - 15x²

= (7x⁴ – 5x⁴) + [(-35). x³ + 35x³ ] – 15x² + 14x

= 2x⁴ + 0 - 15x² + 14x

= 2x⁴ – 15x² + 14x

b) Thay x = $- \frac{1}{2}$ vào P(x), ta được:

P( $- \frac{1}{2}$ ) = 2. ( $- \frac{1}{2}$ )⁴ – 15. ( $- \frac{1}{2}$ )² + 14.( $- \frac{1}{2}$ )

$\begin{array}{l} = 2. \frac{1}{16} - 15. \frac{1}{4} + 14. (\frac{- 1}{2}) \\ = \frac{1}{8} - \frac{15}{4} - 7 \\ = \frac{1}{8} - \frac{30}{8} - \frac{56}{8} \\ = \frac{85}{8} \end{array}$

Thử thách nhỏ trang 37 Toán lớp 7: Rút gọn biểu thức x³(x+2) – x(x³ + 2³) – 2x(x² – 2²)

Phương pháp giải:

Bước 1: Nhân đơn thức với đa thức: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.

Bước 2: Trừ các đa thức thu được

Lời giải:

Ta có:

x³(x+2) – x(x³ + 2³) – 2x(x² – 2²)

= x³ . x + x³ . 2 – (x . x³ + x . 2³) – ( 2x . x² – 2x . 2²)

= x⁴ + 2x³ – (x⁴ + 8x ) – (2x³ – 8x)

= x⁴ + 2x³ – x⁴ – 8x – 2x³ + 8x

= (x⁴ – x⁴) + (2x³ – 2x³) + (-8x + 8x)

= 0

2. Nhân đa thức với đa thức

HĐ 3 trang 37 Toán lớp 7: Tính (2x – 3) . (x² – 5x + 1) bằng cách thực hiện các bước sau:

Bước 1: Nhân 2x với đa thức x² – 5x + 1

Bước 2: Nhân (-3) với đa thức x² – 5x + 1

Bước 3: Cộng các đa thức thu được ở hai bước trên và thu gọn

Kết quả thu được là tích của đa thức 2x – 3 với đa thức x² – 5x + 1

Phương pháp giải:

Thực hiện theo 3 bước trên

Lời giải:

Ta có:

(2x – 3) . (x² – 5x + 1)

= 2x. (x² – 5x + 1) + (-3). (x² – 5x + 1)

= 2x . x² + 2x . (-5x) + 2x . 1 + (-3).x² + (-3).(-5x) + (-3). 1

= 2x³ + (-10x² ) + 2x + (-3x²) + 15x + (-3)

= 2x³ + (-10x² + -3x²) + (2x + 15x) + (-3)

Giải Toán 7 trang 38 Tập 2

Luyện tập 2 trang 38 Toán lớp 7: Tính (x³ – 2x² + x – 1)(3x – 2). Trình bày lời giải theo 2 cách.

Phương pháp giải:

Cách 1: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau

Cách 2: Đặt tính nhân:

+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trng một dòng riêng.

+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau để thực hiện phép cộng theo cột.

Lời giải:

Cách 1:

(x³ – 2x² + x – 1) (3x – 2)

= x³ . (3x – 2) + (-2x²) .(3x – 2) + x .(3x – 2) + (-1) . (3x – 2)

= x³ . 3x + x³ . (-2) + (-2x²). 3x + (-2x²) . (-2) + x . 3x + x. (-2) + (-1). 3x + (-1). (-2)

= 3x⁴ – 2x³ – 6x³ + 4x² + 3x² – 2x – 3x + 2

= 3x⁴ + (-2x³ -6x³) + (4x² + 3x² ) + (-2x – 3x) + 2

= x⁴ + (-8x³) + 7x² + (-5x) + 2

= x⁴– 8x³ +7x² – 5x + 2

Cách 2:

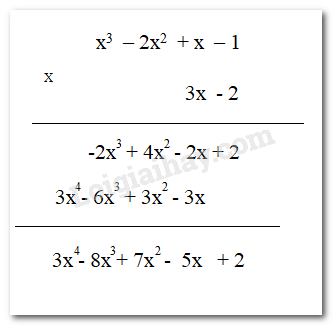
Luyện tập 2 trang 38 Toán lớp 7 Tập 2 | Kết nối tri thức (ảnh 1)

Vận dụng 2 trang 38 Toán lớp 7: Rút gọn biểu thức (x – 2) . (2x³ – x² + 1) + (x – 2) x²(1 – 2x)

Phương pháp giải:

Sử dụng tính chất phân phối của phép nhân đối với phép cộng

Lời giải:

(x – 2) . (2x³ – x² + 1) + (x – 2) x²(1 – 2x)

= (x – 2). [(2x³ – x² + 1) + x²(1 – 2x)]

= (x – 2). [2x³ – x² + 1 + x² . 1 + x² . (-2x)]

= (x – 2) . (2x³ – x² + 1 + x² – 2x³)

= (x – 2) .1

= x – 2

Vận dụng 3 trang 38 Toán lớp 7: Trở lại bài toán đoán tuổi, để giải thích bí mật trong bài toán đoán tuổi của anh Pi, em hãy thực hiện các yêu cầu sau:

* Gọi x là tuổi cần đoán. Tìm đa thức ( biến x) biểu thị kết quả thứ nhất và kết quả thứ hai

* Tìm đa thức biểu thị kết quả cuối cùng.

Từ đó hãy nêu cách tìm x.

Phương pháp giải:

Tìm đa thức biểu thị từng kết quả thứ nhất và thứ hai

Lấy kết quả thứ nhất trừ đi kết quả thứ hai

Lời giải:

Đa thức biểu thị kết quả thứ nhất: K = (x + 1)²

Đa thức biểu thị kết quả thứ hai: H = (x – 1)²

Đa thức biểu thị kết quả cuối cùng:

Q = K – H = (x + 1)² - (x – 1)²

= (x+1).(x+1) - (x – 1). (x – 1)

= x.(x+1) + 1.(x+1) - x(x-1) + (-1). (x-1)

= x.x + x.1 + 1.x + 1.1 –[ x.x – x .1 + (-1).x + (-1) . (-1)]

= x² + x + x + 1 – (x² – x – x + 1)

= x² + x + x + 1 – x² + x + x – 1

= (x² - x² ) + (x+x+x+x) + (1- 1)

= 4x

Để tìm x, ta lấy kết quả cuối cùng chia cho 4

Bài tập

Bài 7.23 trang 38 Toán lớp 7: Thực hiện các phép nhân sau:

a) 6x² . (2x³ – 3x² + 5x – 4)

b) (-1,2x²) . (2,5x⁴ – 2x³ + x² – 1,5)

Phương pháp giải:

Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.

Lời giải:

a) 6x² . (2x³ – 3x² + 5x – 4)

= 6x² . 2x³ +6x² . (-3x²) + 6x² . 5x + 6x² .(-4)

= 12x⁵ – 18x⁴ + 30x³ – 24x²

b) (-1,2x²) . (2,5x⁴ – 2x³ + x² – 1,5)

= (-1,2x²) . 2,5x⁴ + (-1,2x²) . (-2x³) + (-1,2x²) . x² + (-1,2x²) . (-1,5)

= -3x⁶ + 2,4x⁵ – 1,2x⁴ + 1,8x²

Bài 7.24 trang 38 Toán lớp 7: Rút gọn các biểu thức sau:

a) 4x²(5x² + 3) – 6x(3x³ – 2x + 1) – 5x³ (2x – 1)

b) $\frac{3}{2} x (x^{2} - \frac{2}{3} x + 2) - \frac{5}{3} x^{2} (x + \frac{6}{5})$

Phương pháp giải:

Bước 2: Trừ các đa thức thu được

Lời giải:

a) 4x²(5x² + 3) – 6x(3x³ – 2x + 1) – 5x³ (2x – 1)

= 4x² . 5x² + 4x² . 3 – [6x . 3x³ + 6x . (-2x) + 6x . 1] – [5x³ . 2x + 5x³ . (-1)]

= 20x⁴ + 12x² – (18x⁴ – 12x² + 6x) – (10x⁴ – 5x³)

= 20x⁴ + 12x² - 18x⁴ + 12x² - 6x - 10x⁴ + 5x³

= (20x⁴ – 18x⁴ - 10x⁴ ) + 5x³ + (12x² + 12x² ) – 6x

= -8x⁴ + 5x³ + 24x² – 6x

$\begin{array}{l} b) \frac{3}{2} x (x^{2} - \frac{2}{3} x + 2) - \frac{5}{3} x^{2} (x + \frac{6}{5}) \\ = \frac{3}{2} x . x^{2} + \frac{3}{2} x . (- \frac{2}{3} x) + \frac{3}{2} x .2 - (\frac{5}{3} x^{2} . x + \frac{5}{3} x^{2} . \frac{6}{5}) \\ = \frac{3}{2} x^{3} - x^{2} + 3 x - (\frac{5}{3} x^{3} + 2 x^{2}) \\ = \frac{3}{2} x^{3} - x^{2} + 3 x - \frac{5}{3} x^{3} - 2 x^{2} \\ = (\frac{3}{2} x^{3} - \frac{5}{3} x^{3}) + (- x^{2} - 2 x^{2}) + 3 x \\ = \frac{- 1}{6} x^{3} - 3 x^{2} + 3 x \end{array}$

Bài 7.25 trang 38 Toán lớp 7: Thực hiện phép nhân sau:

a) (x² – x) . (2x² – x – 10)

b) (0,2x² – 3x) . 5(x² -7x + 3)

Phương pháp giải:

Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau

Lời giải:

a) (x² – x) . (2x² – x – 10)

= x² . (2x² – x – 10) – x. (2x² – x – 10)

= x² . 2x² + x² . (-x) + x² .10 – [ x. 2x² + x. (-x) + x. (-10)]

= 2x⁴ – x³ + 10x² – (2x³ – x² – 10x)

= 2x⁴ – x³ + 10x² – 2x³ + x² + 10x

= 2x⁴ + (– x³ – 2x³ ) + 10x² + 10x

= 2x⁴ – 3x³ + 10x² + 10x

b) (0,2x² – 3x) . 5(x² -7x + 3)

= (0,2x² . 5 – 3x . 5) . (x² -7x + 3)

= (x² – 15x). (x² -7x + 3)

= x² . (x² -7x + 3) – 15. (x² -7x + 3)

= x² . x² + x² . (-7x) + x² . 3 – [ 15x² + 15.(-7x) + 15.3]

= x⁴ – 7x³ + 3x² – (15x² – 105x + 45)

= x⁴ – 7x³ + 3x² – 15x² + 105x – 45

= x⁴ – 7x³ + (3x² – 15x²) + 105x – 45

= x⁴ – 7x³ – 12x² + 105x – 45

Bài 7.26 trang 38 Toán lớp 7: a) Tính (x² – 2x + 5) . (x – 2)

b) Từ đó hãy suy ra kết quả phép nhân (x² – 2x + 5) . (2– x). Giải thích cách làm.

Phương pháp giải:

Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau

Lời giải:

a) Ta có:

(x² – 2x + 5) . (x – 2)

= x² . (x – 2) – 2x . (x – 2) + 5. (x – 2)

= x² . x + x² . (-2) – [2x. x + 2x.(-2) ] + 5.x + 5. (-2)

= x³ – 2x² – (2x² – 4x) +5x – 10

= x³ – 2x² – 2x² + 4x +5x – 10

= x³ +(– 2x² – 2x² )+ (4x +5x) – 10

= x³ – 4x² + 9x – 10

b) Vì (x² – 2x + 5) . (2– x) = (x² – 2x + 5) . [-(x– 2)] = - (x² – 2x + 5) . (x – 2)

Do đó, (x² – 2x + 5) . (2– x) = - (x³ – 4x² + 9x – 10) = -x³ + 4x² - 9x + 10

Bài 7.27 trang 38 Toán lớp 7: Giả sử ba kích thước của một hình hộp chữ nhật là x; x +1; x – 1 (cm) với x > 1. Tìm đa thức biểu thị thể tích (đơn vị: cm³) của hình hộp chữ nhật đó.

Phương pháp giải:

+ Thể tích hình hộp chữ nhật = chiều dài . chiều rộng . chiều cao

+ Nhân các đa thức

Lời giải:

Đa thức biểu thị thể tích hình hộp chữ nhật đó là:

V = x . (x + 1) . (x – 1)

= (x.x + x.1) . (x – 1)

= (x² + x) . (x – 1)

= x² . (x -1) + x .(x – 1)

= x² . x + x² . (-1) + x.x + x . (-1)

= x³ – x² + x² – x

= x³ - x

Bài 7.28 trang 38 Toán lớp 7: Thực hiện các phép nhân hai đa thức sau:

a) 5x³ – 2x² + 4x – 4 và x³ + 3x² – 5

b) -2,5.x⁴ + 0,5x² + 1 và 4x³ – 2x + 6

Phương pháp giải:

Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau

Lời giải:

a) (5x³ – 2x² + 4x – 4) . ( x³ + 3x² – 5)

= 5x³ . ( x³ + 3x² – 5) - 2x² . ( x³ + 3x² – 5) + 4x . ( x³ + 3x² – 5) – 4 . ( x³ + 3x² – 5)

= 5x³ . x³ + 5x³ . 3x² + 5x³ . (-5) – [ 2x² . x³ + 2x² . 3x² +2x² . (-5)] + [4x . x³ + 4x. 3x² + 4x . (-5)] – [ 4x³ + 4.3x² + 4.(-5)]

= 5x⁶ + 10x⁵ – 25x³ – (2x⁵ + 6x⁴ – 10x²) + 4x⁴ + 12x³ – 20x – (4x³ + 12x² – 20)

= 5x⁶ + 10x⁵ – 25x³ – 2x⁵ - 6x⁴ + 10x² + 4x⁴ + 12x³ – 20x – 4x³ - 12x² + 20

= 5x⁶ + (10x⁵ – 2x⁵ ) + (- 6x⁴ + 4x⁴ ) + (-25x³ + 12x³ – 4x³ ) + (10x² - 12x² ) – 20x + 20

= 5x⁶ + 8x⁵ – 2x⁴ – 17x³ -2x² – 20x + 20

b) (-2,5.x⁴ + 0,5x² + 1) . (4x³ – 2x + 6)

= -2,5.x⁴ . (4x³ – 2x + 6) + 0,5x² . (4x³ – 2x + 6) + 1. (4x³ – 2x + 6)

= (-2,5.x⁴) . 4x³ + (-2,5.x⁴ ) . (-2x) + (-2,5.x⁴ ) . 6 + 0,5x² . 4x³ + 0,5x² . (-2x) + 0,5x² . 6 + 4x³ – 2x + 6

= -10x⁷ + 5x⁵ – 15x⁴ + 2x⁵ – x³ + 3x² + 4x³ – 2x + 6

= -10x⁷ + ( 5x⁵ + 2x⁵ ) - 15x⁴ + (– x³ + 4x³ ) + 3x² – 2x + 6

= -10x⁷ +7x⁵ - 15x⁴ + 3x³ + 3x² – 2x + 6

Bài 7.29 trang 38 Toán lớp 7: Người ta dùng những chiếc cọc để rào một mảnh vườn hình chữ nhật sao cho mỗi góc vườn đều có một chiếc cọc và hai cọc liên tiếp cắm cách nhau 0,1 m. Biết rằng số cọc dùng để rào hết chiều dài của vườn nhiều hơn số cọc dùng để rào hết chiều rộng là 20 chiếc. Gọi số cọc dùng để rào hết chiều rộng là x . Tìm đa thức biểu thị diện tích của vườn đó.

Phương pháp giải:

Biểu thị số cọc để rào hết chiều dài

Tìm đa thức biểu thị chiều rộng, chiều dài.

Tìm đa thức biểu thị diện tích mảnh vườn = chiều dài . chiều rộng

Lời giải:

Vì số cọc để rào hết chiều dài của vườn nhiều hơn số cọc dùng để rào hết chiều rộng là 20 chiếc nên số cọc dùng để rào chiều dài là: x + 20

Do mỗi góc vườn đều có một chiếc cọc và hai cọc liên tiếp cắm cách nhau 0,1 m nên:

Chiều rộng của mảnh vườn là: 0,1 . (x – 1) = 0,1x – 0,1

Chiều dài của mảnh vườn là: 0,1 . (x + 20 – 1) = 0,1(x + 19) = 0,1x + 1,9

Đa thức biểu diễn diện tích mảnh vườn là:

S = (0,1x – 0,1) . (0,1x + 1,9)

= 0,1x . (0,1x + 1,9) – 0, 1. (0,1x + 1,9)

= 0,1x . 0,1x + 0,1x . 1,9 – (0,1.0,1x + 0,1. 1,9)

= 0,01x² + 1,9x – (0,01x + 0,19)

= 0,01x² + 1,9x – 0,01x - 0,19

= 0,01x² + 1,89x – 0,19

Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung trang 34

Bài 28: Phép chia đa thức một biến

Luyện tập chung trang 44

Bài tập cuối chương 7

Lý thuyết Phép nhân đa thức một biến

1. Nhân đơn thức với đa thức

Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức vời từng hạng tử của đa thức rồi cộng các tích với nhau.

Ví dụ:

Muốn tính $(- 3 x^{2}) \cdot (x^{3} - \frac{1}{3} x + 4)$ ta làm như sau:

$(- 3 x^{2}) \cdot (x^{3} - \frac{1}{3} x + 4)$ = $(- 3 x^{2}) \cdot (x^{3}) + (- 3 x^{2}) \cdot (- \frac{1}{3} x) + (- 3 x^{2}) \cdot 4$

= – 3x⁵ + x³ – 12x².

2. Nhân đa thức với đa thức

Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

Ví dụ:

Muốn tính (x + 2).(3x² – 4x + 5) ta làm như sau:

(x + 2).(3x² – 4x + 5) = x.(3x² – 4x + 5) + 2.(3x² – 4x + 5)

= x.3x² + x.( – 4x) + x.5 + 2.3x² +2.( – 4x) + 2.5

= 3x³– 4x² + 5x + 6x² – 8x + 10

= 3x³ + (– 4x² + 6x²) + (5x – 8x) + 10

= 3x³ + 2x² – 3x + 10.

Chú ý:

• Ta có thể trình bày phép nhân một đa thức với một đa thức bằng cách đặt tính.

Khi trình bày theo cách này ta cần:

+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng.

+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau (để thực hiện phép cộng theo cột).

+ Khi nhân các hạng tử ở dòng dưới với đa thức ở dòng trên, ta nên nhân các hạng tử theo thứ tự từ bậc thấp đến bậc cao.

Chẳng hạn: Đặt tính nhân (x + 3).(2x² – 3x – 5), ta làm như sau:

Lý thuyết Toán 7 Kết nối tri thức Bài 27: Phép nhân đa thức một biến (ảnh 1)

• Phép nhân đa thức cũng có các tính chất:

+ Giao hoán: A.B = B.A.

+ Kết hợp: (A.B).C = A.(B.C).

+ Phân phối đối với phép cộng: A.(B + C) = A.B + A.C.

Từ khóa :

Giải bài tập toán 7

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

165

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

141

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm