Cho tứ giác ABCD có M, N lần lượt là trung điểm của AD, BC. Chứng minh: .MN < (AB +CD)/ 2

Van Anh Ngày: 21-11-2023 Lớp 8
759
759

Với giải Bài 20* trang 66 SBT Toán lớp 8 Cánh diều chi tiết trong Bài 3: Đường trung bình của tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 3: Đường trung bình của tam giác

Bài 20* trang 66 SBT Toán 8 Tập 2: Cho tứ giác ABCD có M, N lần lượt là trung điểm của AD, BC. Chứng minh: MN≤AB+DC2. Dấu đẳng thức xảy ra khi nào?

Lời giải:

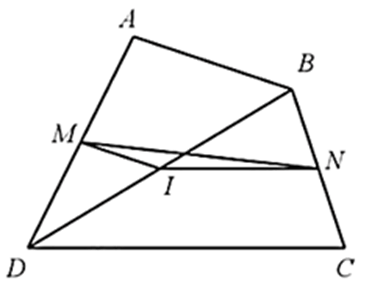
Cho tứ giác ABCD có M, N lần lượt là trung điểm của AD, BC

Lấy I là trung điểm của BD.

Xét ∆ABD có M, I lần lượt là trung điểm của AD, BD nên MI là đường trung bình của ∆ABD

Suy ra MI // AB và MI=AB2.

Xét ∆BDC có N, I lần lượt là trung điểm của BC, BD nên NI là đường trung bình của ∆BDC

Suy ra NI // CD và NI=CD2.

Do đó MI+NI=AB+CD2 (1).

• Nếu I không thuộc MN thì MNI là tam giác nên ta có MN < MI + NI (bất đẳng thức tam giác).

• Nếu I thuộc MN ta có MN = MI + NI.

Tức là, ta luôn có MN ≤ MI + NI (2).

Từ (1), (2) suy ra MN≤AB+CD2.

Dấu đẳng thức xảy ra khi I thuộc MN, khi đó AB // MI // CD.

Vậy dấu đẳng thức xảy ra khi AB // CD.

 

Xem thêm lời giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 14 trang 65 SBT Toán 8 Tập 2: Chọn phát biểu đúng trong các phát biểu sau:...

Bài 15 trang 65 SBT Toán 8 Tập 2: Hình 21 cho biết cạnh của tam giác đều ABC bằng 6 cm; M, N lần lượt là trung điểm các cạnh AB, AC. Chỉ ra phát biểu sai trong các phát biểu sau:..

Bài 16 trang 65 SBT Toán 8 Tập 2: Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh:....

Bài 17 trang 65 SBT Toán 8 Tập 2: Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân ABC (AB = AC = 2 m) cùng các thanh sắt nằm ngang GF, HE, ID, BC và sau đó gắn cây thông như Hình 22. Tính số tiền sắt cần sử dụng để làm cây thông noel đó.....

Bài 18 trang 66 SBT Toán 8 Tập 2: Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD). Gọi I, K, M lần lượt là trung điềm của BH, CH, AD. Chứng minh:....

Bài 19* trang 66 SBT Toán 8 Tập 2: Cho tứ giác ABCD có AD = BC. Đường thẳng đi qua trung điểm M và N lần lượt của các cạnh AB và CD cắt các đường thẳng AD và BC lần lượt tại E và F. Chứng minh: AEM^=MFB^....

Bài 20* trang 66 SBT Toán 8 Tập 2: Cho tứ giác ABCD có M, N lần lượt là trung điểm của AD, BC. Chứng minh: MN≤AB+DC2. Dấu đẳng thức xảy ra khi nào?...

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Xem thêm các nội dung khác:

Đánh giá

0

0 đánh giá

Đánh giá
Bài viết cùng môn học
Toán Tổng hợp kiến thức
Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6
Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6 Lữ Ngọc My My
55
Toán Tổng hợp kiến thức
3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1
3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1 Lữ Ngọc My My
52
Toán Tổng hợp kiến thức
Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84
Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84 Lữ Ngọc My My
42
Toán Tổng hợp kiến thức
Tìm x; y nguyên 2xy + 2x - y = 8
Tìm x; y nguyên 2xy + 2x - y = 8 Lữ Ngọc My My
43

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.

DMCA.com Protection Status