Với giải sách bài tập Toán 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit
Bài 1 trang 22 SBT Toán 11 Tập 2: Giải các phương trình sau:
a) ;
b) 52x = 10;
c) 3x = 18;
d) ;
e) 53x = 25x – 2;
g) .
Lời giải:
a) 32x + 1 = 3– 3
⇔ 2x + 1= –3 (do 3 > 1)
⇔ x = – 2.
Vậy phương trình có nghiệm là x = 2.
b) 52x =10
⇔ 2x = log5 10
⇔ x = .
Vậy phương trình có nghiệm là x = .
c) 3x = 18 ⇔ x = log3 18
Vậy phương trình có nghiệm là x = log3 18.
d)
⇔
⇔ 1 - x = (do 5 > 1)
⇔ x =
Vậy phương trình có nghiệm là x = .
e) 53x = 25x–2
⇔ 53x = 52x–4
⇔ 3x = 2x – 4 (do 5 > 1)
⇔ x = – 4.
Vậy phương trình có nghiệm là x = – 4.
g)
⇔
⇔
⇔ –3x – 3 = –5x + 5 (do 2 > 1)
⇔ 2x = 8 ⇔ x = 4.
Vậy phương trình có nghiệm là x = 4.
Bài 2 trang 22 SBT Toán 11 Tập 2: Giải các phương trình sau:
a) log3 (2x - 1) = 3;
b) log49 x = 0,25;
c) log2 (3x + 1) = log2 (2x - 4);
d) log5 (x - 1) + log5 (x - 3) = log5 (2x + 10);
e) log x + log (x – 3) = 1;
g) log2 (log81 x) = -2.
Lời giải:
a) Điều kiện: 2x – 1 > 0
Ta có: log3 (2x - 1) = 3
⇔ 2x - 1 = 33 = 27
⇔ x = 14 (nhận)
Vậy tập nghiệm của phương trình là: S = {14}.
b) Điều kiện: x > 0
Ta có: log49 x = 0,25
⇔
⇔
⇔
⇔ x = (nhận)
Vậy tập nghiệm của phương trình là: S = {}.
c) Điều kiện:
Ta có: log2 (3x + 1) = log2 (2x - 4)
⇔ 3x + 1 = 2x – 4 (do 2 >1)
⇔ x = – 5 (loại).
Vậy phương trình đã cho vô nghiệm.
d) Điều kiện:
Ta có: log5 (x - 1) + log5 (x - 3) = log5 (2x + 10)
⇔
⇔
⇔ x2 – 4x + 3 = 2x + 10 (do 2 >1)
⇔ x2 – 6x – 7 = 0.
⇔ x = 7 (nhận) hoặc x = –1 (loại)
Kết hợp điều kiện, vậy tập nghiệm của phương trình là: S = {7}.
e) Điều kiện:
Ta có: log x + log (x – 3) = 1
⇔ log [x(x – 3)] = 1
⇔ log (x2 – 3x)=1
⇔ x2 – 3x – 10 = 0 (do 10 >1)
⇔ x = 5 (nhận) hoặc x = –2 (loại)
Kết hợp điều kiện, vậy tập nghiệm của phương trình là: S = {5}.
g) Điều kiện:
Ta có: log2 (log81 x) = -2
⇔ log81 x = 2-2 ⇔ x = = 3 (nhận)
Kết hợp điều kiện, vậy tập nghiệm của phương trình là: S = {3}.
Bài 3 trang 22 SBT Toán 11 Tập 2: Giải các bất phương trình sau:
a) ;
b) ;
c) ;
d) 42x < 8x –1;
e) ;
g) 0,25x – 2 > 0,5x + 1.
Lời giải:
a) Ta có:
⇔
⇔
⇔
⇔ .
Vậy tập nghiệm của bất phương trình là: S = .
b) Ta có:
⇔
⇔ (do 3 > 1)
⇔ x ≤ 5
Vậy tập nghiệm của bất phương trình là: S = (-∞; 5].
c)
⇔ 2-x < 8
⇔ 2-x < 23
⇔ x > -3
Vậy tập nghiệm của bất phương trình là: S = (-3; +∞).
d) 42x < 8x – 1
⇔ 24x < 23x – 3
⇔ 4x < 3x – 3 (do 2 > 1)
⇔ x < – 3.
Vậy tập nghiệm của bất phương trình là: S = (-∞; -3).
e)
⇔ 5x-2 ≤ 5-2x
⇔ x - 2 ≤ -2x (do 5 >1)
⇔ 3x ≤ 2 ⇔ x ≤
Vậy tập nghiệm của bất phương trình là: S = .
g) 0,25x – 2 > 0,5x + 1
⇔ 0,52(x - 2) > 0,5x + 1
⇔ 2(x –2) < x +1 (do 0 < 0,5 < 1)
⇔ x < 5.
Vậy tập nghiệm của bất phương trình là: S = (-∞; 5).
Bài 4 trang 22 SBT Toán 11 Tập 2: Giải các bất phương trình sau:
a) log3 (x + 4) < 2;
b) ;
c) ;
d) ;
e) ;
g) .
Lời giải:
a) Điều kiện: x > –4
Ta có: log3 (x + 4) < 2 ⇔ x + 4 < 9 ⇔ x < 5
Kết hợp điều kiện, vậy tập nghiệm của bất phương trình là: S = (–4; 5).
b) Điều kiện: x > 0
Ta có:
Kết hợp điều kiện, vậy tập nghiệm của bất phương trình là: S = .
c) Điều kiện: x > 1
Ta có: log0,25 (x - 1) ≤ -1
⇔ x - 1 ≥ (0,25)-1 (do 0 < 0, 5 < 1)
⇔ x - 1 ≥ 4
⇔ x ≥ 5
Kết hợp điều kiện, vậy tập nghiệm của bất phương trình là: S = .
d) Điều kiện:
Ta có:
⇔ x2 - 24x ≥ 25
⇔ x2 - 24x - 25 ≥ 0 (Do 5 > 1)
⇔
Kết hợp điều kiện, vậy tập nghiệm của bất phương trình là: S = .
e) Điều kiện:
Ta có:
⇔
⇔ x2 + 2x + 1 ≤ 3x + 7 (do cơ số )
⇔ x2 - x - 6 ≤ 0 ⇔ -2 ≤ x ≤ 3
Kết hợp điều kiện, vậy tập nghiệm của phương trình là: S = (−1; 3].
g) Điều kiện:
Ta có:
⇔
⇔
⇔ (do cơ số 2 > 1)
⇔ (x + 1)2 ≤ 3x + 21
⇔ x2 + 2x + 1 ≤ 3x + 21
⇔ x2 - x - 20 ≤ 0
⇔ -4 ≤ x ≤ 5
Kết hợp điều kiện, vậy tập nghiệm của phương trình là: S = (–1; 5].
Bài 5 trang 22 SBT Toán 11 Tập 2: Giải các phương trình sau:
a) 4x – 5.2x + 4 = 0;
b) ;
Lời giải:
a) 4x – 5.2x + 4 = 0;
Đặt t = 2x (t > 0).
Khi đó: t2 – 5t + 4 = 0 ⇔
=> .
Kết hợp với điều kiện, vậy phương trình có nghiệm x = 0 hoặc x = 2.
b)
⇔
⇔
Đặt t = (t > 0).
Khi đó, ta có: t2 - 6t + 27 ⇔ t = 9 (nhận) hoặc t = –3 (loại)
Do đó = 9 ⇔ 3–x = 32 ⇔ x = –2.
Vậy nghiệm của phương trình là x = –2.
Lời giải:
Từ giả thiết, nhận được 1 < log3 x < 2 hay 3 < x < 9.
Do đó, ta có các số nguyên cần tìm là 4; 5; 6; 7; 8.
Bài 7 trang 23 SBT Toán 11 Tập 2: Tìm tập xác định của các hàm số:
a) y = f(x) = ;
b) y = f(x) = .
Lời giải:
a) y = f(x) =
Điều kiện xác định:
Tập xác định: D = (1; 2].
b) y = f(x) =
Điều kiện xác định:
=>
Tập xác định: D = (2; 3].
Lời giải:
Ta có f(b) - f(a) = log2 b - log2 a = = 5
⇔ = 25 = 32.
Vậy = 32
P = 3a + 2b.
Lời giải:
Ta có: 125a . 25b = 3
⇔ 53a . 52b = 3
⇔ 53a+2b = 3
⇔ 3a + 2b = log5 3.
Lời giải:
Lượng Uranium - 235 còn lại bằng 90% so với ban đầu là 90 g.
Khi đó M = 90 g, ta có phương trình:
= 0,9
⇔ ⇔ t = (năm).
Vậy sau khoảng 106 979 777 năm thì lượng Uranium-235 còn lại bằng 90% so với ban đầu.
Lời giải:
=>
Để số lượng vi khuẩn trong mỗi milit nước trong thùng ít hơn hoặc bằng 1 000, ta có:
⇔
⇔ = (giờ).
Vậy sau khoảng 10,8 giờ thì số lượng vi khuẩn trong mỗi mililit nước trong thùng ít hơn hoặc bằng 1 000.
Lời giải:
Ta có: pHA = – log xA; pHB = – log xB
Khi đó pHA – pHB = – logxA + logxB =
Do đó (lần)
Vậy dung dịch B có nồng độ ion H+ gấp 5 lần nồng độ ion H+ của dung dịch A.
Xem thêm các bài giải SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Các quy tắc tính đạo hàm
Lý thuyết Phương trình, bất phương trình mũ và lôgarit
1. Phương trình mũ cơ bản
Phương trình mũ cơ bản có dạng (với ).
- Nếu b > 0 thì phương trình có nghiệm duy nhất .
- Nếu b 0 thì phương trình vô nghiệm.
Chú ý: Với
a) .
b) Tổng quát hơn,
Minh họa bằng đồ thị:
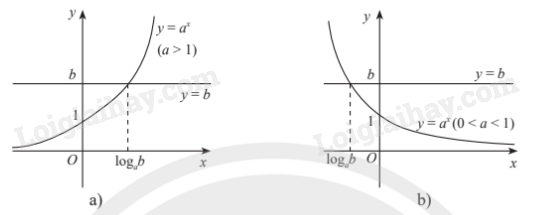
2. Phương trình lôgarit cơ bản
Phương trình lôgarit cơ bản có dạng .
Phương trình luôn có nghiệm duy nhất .
Chú ý: Với
a) .
b) .
Có thể thay bằng (chọn bất phương trình đơn giản hơn)
Minh họa bằng đồ thị:
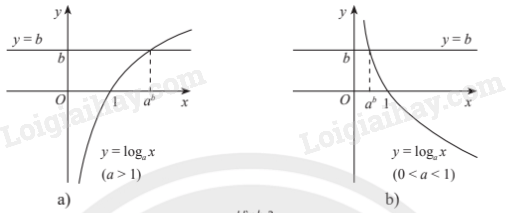
3. Bất phương trình mũ cơ bản
Bất phương trình mũ cơ bản có dạng (hoặc ) với .
Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:
Nếu a > 1 thì .
Nếu 0 < a < 1 thì .
4. Bất phương trình lôgarit cơ bản
Bất phương trình lôgarit cơ bản có dạng (hoặc ) với .
Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:
Nếu a > 1 thì .
Nếu 0 < a < 1 thì .