Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit chi tiết sách Toán 11 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit
(Nguồn:https://www.britannica.com/science/carbon-14)
Việc tính toán tuổi của hoá thạch được thực hiện như thế nào?
Lời giải:
Lượng carbon-14 trong hóa thạch được tính theo công thức , trong đó M0 là lượng carbon-14 có trong cơ thể sinh vật khi chết, t là thời gian tính theo năm kể từ khi sinh vật chết đến khi khảo sát. Từ đây, nếu biết M và M0 thì tìm được t.
1. Phương trình mũ
(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, năm 2017, trang 101)
a) Ban đầu mẻ có bao nhiêu cá thể vi khuẩn?
b) Sau 1 giờ thì mẻ có 100 cá thể vi khuẩn. Tìm giá trị của k (làm tròn kết quả đến hàng phần mười).
c) Sau bao lâu thì số lượng cá thể vi khuẩn đạt đến 50000?
Lời giải:
a) Số cá thể vi khuẩn ban đầu mẻ có là:
P(0)=50.10k.0=50.100=50 (cá thể)
Vậy ban đầu mẻ có 50 cá thể vi khuẩn.
b) Với t=1,P(t)=100ta có:
P(1)=50.10k.1⇔100=50.10k⇔10k=2⇔k=log2≈0,3.
Vậy k≈0,3.
c) Thời gian để số lượng cá thể vi khuẩn đạt đến 50000 là:
50000=50.100,3t⇔100,3t=1000
⇔0,3t=log1000⇔0,3t=3⇔t=10(giờ)
Vậy sau 10 giờ thì số lượng cá thể vi khuẩn đạt đến 50000.
Giải Toán 11 trang 27 Tập 2
Lời giải:
•Khi b>0, đồ thị của hai hàm số y=ax và y=b cắt nhau tại một điểm duy nhất.
Khi đó, phương trình ax=b có nghiệm duy nhất x=logab.
•Khi b≤0, đồ thị của hai hàm số y=ax và y=b không có điểm chung.
Khi đó, phương trình ax=b vô nghiệm.
Thực hành 1 trang 28 Toán 11 Tập 2: Giải các phương trình sau:
a) ;
Lời giải:
a)
;
b) ;
c)
.
(Nguồn: https://pubchem.ncbi.nlm.nih.gov/elemene/Plutonium#section=Atomic-
Mass-Half-Life-and-Decay)
Từ khối lượng ban đầu 200 g, sau bao lâu thì khối lượng plutonium-234 còn lại là:
a) 100 g? b) 50 g? c) 20 g?
Lời giải:
a) Với M0 = 200, T = 9 , M(t) = 100, ta có:
.
Vậy sau 9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 100 g.
b) Với M0 = 200, T = 9 , M(t) = 50, ta có:
Vậy sau 18 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 50 g.
c) Với M0 = 200, T = 9 , M(t) = 20, ta có:
.
Vậy sau khoảng 29,9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 20 g.
2. Phương trình lôgarit
Biết sữa có độ pH là 6,5. Nồng độ H+ của sữa bằng bao nhiêu?
Lời giải:
Ta có pH = −log x ⇔ 6,5 = −log x
⇔ log x = −6,5 ⇔ x = 10−6,5 ≈ 3,16.10−7.
Vậy nồng độ H+ của sữa bằng 3,16.10−7 mol/L.
Giải Toán 11 trang 29 Tập 2
Lời giải:
Đồ thị của hai hàm số y=logax và y=b luôn cắt nhau tại một điểm duy nhất.
Khi đó, phương trình logax=b có nghiệm duy nhất x=ab.
Thực hành 2 trang 30 Toán 11 Tập 2: Giải phương trình sau:
a) ;
b) .
Lời giải:
a)
Điều kiện x – 2 > 0 ⇔ x > 2.
Khi đó
(TM)
Vậy phương trình đã cho có nghiệm là x = 6.
b) .
Điều kiện
Khi đó
(TM).
Vậy phương trình đã cho có nghiệm là x = 4.
3. Bất phương trình mũ
Hoạt động khám phá 5 trang 30 Toán 11 Tập 2: Xét quần thể vi khuẩn ở Hoạt động khám phá 1.
a) Ở những thời điểm nào thì số lượng cá thể vi khuẩn vượt quá 50 000?
b) Ở những thời điểm nào thì số lượng cá thể vi khuẩn vượt quá 50 000 nhưng chưa vượt quá 100 000?
Lời giải:
Do 10>1nên hàm số P(t)=50.10kt đồng biến trên ℝ.
a) Tại thời điểm t=10 thì số lượng cá thể vi khuẩn bằng 50000.
Vì hàm số đồng biến trên ℝ nên với t>10 thì số lượng cá thể vi khuẩn vượt quá 50000.
b) Thời gian để số lượng cá thể vi khuẩn đạt đến 100000 là:
100000=50.100,3t⇔100,3t=2000
⇔0,3t=log2000⇔t≈11 (giờ)
•Tại thời điểm t=10 thì số lượng cá thể vi khuẩn bằng 50000.
•Tại thời điểm t=11 thì số lượng cá thể vi khuẩn bằng 100000.
Vì hàm số đồng biến trên ℝ nên với 10<t<11thì số lượng cá thể vi khuẩn vượt quá 50000 nhưng chưa vượt quá 100000.
Thực hành 3 trang 31 Toán 11 Tập 2: Giải các bất phương trình sau:
a)2x > 16;
b) 0,1x ≤ 0,001;
c) .
Lời giải:
a) 2x > 16 ⇔ 2x > 24 ⇔ x > 4 (do 2 > 1).
Vậy nghiệm của bất phương trình đã cho là x > 4.
b) 0,1x ≤ 0,001 ⇔ 0,1x ≤ 0,13⇔ x ≥ 3 (do 0 < 0,1 < 1).
Vậy nghiệm của bất phương trình đã cho là x ≥ 3.
c)
(do ).
.
Vậy nghiệm của bất phương trình đã cho là x ≥ −2.
4. Bất phương trình lôgarit
Lời giải:
Ta có .
Do nên hàm số nghịch biến trên (0; +∞).
Độ pH từ 7,3 đến 7,45 hay 7,3 ≤ −log x ≤7,45
⇔ −7,3 ≥ log x ≥ −7,45⇔ 10−7,3 ≥ x ≥ 10−7,45.
Vì hàm số nghịch biến trên (0; +∞) nên nồng độ H+trong máu nhận giá trị trong miền từ 10−7,45 mol/L đến 10−7,3mol/L.
Thực hành 4 trang 32 Toán 11 Tập 2: Giải các bất phương trình sau:
a);
b) .
Lời giải:
a)
Điều kiện: x + 1 > 0 ⇔ x > −1.
.
Vậy nghiệm của bất phương trình đã cho là .
b)
Điều kiện: x + 2 > 0 ⇔ x > −2.
.
Kết hợp với điều kiện, ta được nghiệm của bất phương trình đã cho là −2 < x ≤ 3.
Lời giải:
Ta có 6,5 ≤ pH ≤ 8,5 ⇔6,5 ≤ −log x ≤ 8,5
⇔−6,5 ≥ log x ≥ 8,5 ⇔ 10−6,5 ≥ x ≥ 10−8,5.
Vậy nồng độ H+trong máu nhận giá trị trong miền từ 10−8,5 mol/L đến 10−6,5mol/L.
Bài tập
Bài 1 trang 32 Toán 11 Tập 2: Giải các phương trình sau:
a) 52x – 1 = 25;
Lời giải:
a).
Vậy nghiệm của phương trình đã cho là .
b)3x + 1 = 92x + 1 ⇔ 3x + 1 = 32(2x + 1)
⇔ x + 1 = 2(2x + 1) ⇔ x + 1 = 4x + 2
⇔ 3x = −1 ⇔ .
Vậy nghiệm của phương trình đã cho là .
c) 101 – 2x = 100 000 ⇔ 101 – 2x = 105
⇔ 1 – 2x = 5 ⇔ 2x = – 4 ⇔ x = – 2.
Vậy nghiệm của phương trình đã cho là x = – 2.
Bài 2 trang 33 Toán 11 Tập 2: Giải các phương trình sau. Làm tròn kết quả đến hàng nghìn.
a) 3x + 2 = 7;
b) 3 . 102x + 1 = 5.
Lời giải:
a) 3x + 2 = 7 ⇔ x + 3 = log3 7
⇔ x = –3 + log3 7 ⇔ x ≈ –0,229.
Vậy nghiệm của phương trình đã cho là x ≈ –0,229.
b)
.
Vậy nghiệm của phương trình đã cho là x ≈ –0,389.
Bài 3 trang 33 Toán 11 Tập 2: Giải các phương trình sau:
a) log6 (4x + 4) = 2;
b) log3 x – log3 (x – 2) = 1.
Lời giải:
a) Điều kiện: 4x + 4 > 0 ⇔ x > –1
Khi đó: log6 (4x + 4) = 2 ⇔ 4x + 4 = 62
⇔ 4x + 4 = 36 ⇔ 4x = 32 ⇔ x = 8 (TMĐK)
Vậy nghiệm của phương trình đã cho là x = 8.
b) Điều kiện: 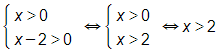
Khi đó: log3 x – log3 (x – 2) = 1
⇔ log3 x – log3 (x – 2) = 1
⇔ log3 x = log3 (x – 2) + 1
⇔ log3 x = log3 (x – 2) + log3 3
⇔ log3 x = log3 3(x – 2)
⇔ x = 3(x – 2) ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Vậy nghiệm của phương trình đã cho là x = 3.
Bài 4 trang 33 Toán 11 Tập 2: Giải các bất phương trình sau:
a);
Lời giải:
a)
(do )
.
Vậy nghiệm của bất phương trình là .
b)
(do 2 > 1)
⇔ x > – 2.
Vậy nghiệm của bất phương trình là x > – 2.
Bài 5 trang 33 Toán 11 Tập 2: Giải các bất phương trình sau:
a)log2 (x – 2) < 2;
b)log (x + 1) ≥ log (2x – 1).
Lời giải:
a) Điều kiện: x – 2 > 0 ⇔ x > 2
Khi đó: log2 (x – 2) < 2⇔ x – 2 < 22
⇔ x – 2 < 4 ⇔ x < 6.
Kết hợp với điều kiện ta được nghiệm của bất phương trình là 2 < x < 6.
b)Điều kiện:
Khi đó: log (x + 1) ≥ log (2x – 1)
⇔x + 1 ≥ 2x – 1 ⇔x ≥ –2⇔x ≤ 2.
Kết hợp với điều kiện ta được nghiệm của bất phương trình là .
(nguồn://pubchem.ncbi.nlm.nih.gov/element/Polonium#section=
Atiomc-Mass-Half-Life-anh-Decay)
a) Khối lượng polonium-210 còn lại bao nhiêu sau 2 năm?
b) Sau bao lâu thì còn lại 40 g polonium-210.
Lời giải:
a) Sau 2 năm (tức t = 730), khối lượng polonium-210 còn lại là:
.
Vậy khối lượng polonium-210 còn lại sau 2 năm khoảng 1,92 g.
b) Ta có
Vậy sau khoảng 182,43 ngày thì còn lại 40 g polonium-210.
(Nguồn: Vật lí 12, NXB Giáo dục Việt Nam, năm 2017, trang 52)
a) Một giáo viên đang giảng bài trong lớp học, có mức cường độ âm là 50 dB. Cường độ âm của giọng nói giáo viên bằng bao nhiêu?
b) Mức cường độ âm trong một nhà xưởng thay đổi trong khoảng từ 75 dB đến 90 dB. Cường độ âm trong nhà xưởng này thay đổi trong khoảng nào?
Lời giải:
a) Ta có
.
Vậy cường độ âm của giọng nói giáo viên bằng 10–7 (W/m2).
b) Ta có
.
Vậy cường độ âm trong nhà xưởng này thay đổi trong khoảng 10–4,5 (W/m2) đến 10–3 (W/m2).
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Các quy tắc tính đạo hàm
Lý thuyết Phương trình, bất phương trình mũ và lôgarit
1. Phương trình mũ cơ bản
Phương trình mũ cơ bản có dạng (với ).
- Nếu b > 0 thì phương trình có nghiệm duy nhất .
- Nếu b 0 thì phương trình vô nghiệm.
Chú ý: Với
a) .
b) Tổng quát hơn,
Minh họa bằng đồ thị:
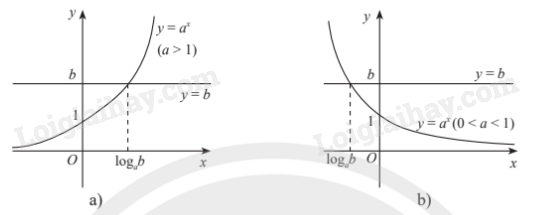
2. Phương trình lôgarit cơ bản
Phương trình lôgarit cơ bản có dạng .
Phương trình luôn có nghiệm duy nhất .
Chú ý: Với
a) .
b) .
Có thể thay bằng (chọn bất phương trình đơn giản hơn)
Minh họa bằng đồ thị:
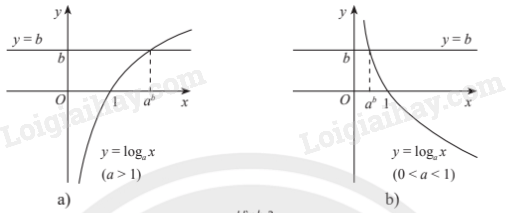
3. Bất phương trình mũ cơ bản
Bất phương trình mũ cơ bản có dạng (hoặc ) với .
Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:
Nếu a > 1 thì .
Nếu 0 < a < 1 thì .
4. Bất phương trình lôgarit cơ bản
Bất phương trình lôgarit cơ bản có dạng (hoặc ) với .
Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:
Nếu a > 1 thì .
Nếu 0 < a < 1 thì .