Với giải sách bài tập Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit
Bài 1 trang 17 SBT Toán 11 Tập 2: Vẽ đồ thị hàm số y = .
Lời giải:
Tập xác định: ℝ.
Do > 1 nên hàm số đồng biến trên ℝ.
Bảng giá trị:
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
|
|
1 |
|
2 |
Đồ thị hàm số đi qua các điểm có tọa độ theo bảng giá trị và nằm phía trên trục hoành.
Từ đó, ta vẽ được đồ thị hàm số như hình vẽ.
Bài 2 trang 17 SBT Toán 11 Tập 2: Vẽ đồ thị hàm số y = .
Lời giải:
Tập xác định: D = (0; +∞)
Do > 1 nên hàm số đồng biến trên (0; +∞).
Bảng giá trị:
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
0 |
|
|
|
|
Đồ thị hàm số đi qua các điểm có tọa độ theo bảng giá trị và nằm phía trên trục hoành.
Từ đó, ta vẽ được đồ thị hàm số như hình vẽ.
Bài 3 trang 17 SBT Toán 11 Tập 2: Tìm tập xác định của các hàm số:
a) y = log2 (x - 4);
b) y = log0,2 (x2 + 2x + 1);
c) y = .
Lời giải:
a) Để hàm số xác định thì x – 4 > 0 ⇒ x > 4.
Tập xác định của hàm số là: D = (4; +∞);
b) Để hàm số xác định thì x2 + 2x + 1 > 0 ⇒ x ≠ 1.
Tập xác định của hàm số là: D = ℝ \ {-1};
c) y = .
Để hàm số xác định thì
Tập xác định của hàm số là: D = .
Bài 4 trang 17 SBT Toán 11 Tập 2: So sánh các cặp số sau:
a) 1,041,7 và 1,042;
b) và ;
c) 1,20,3 và 0,91,8;
d) và 3– 0,2 .
Lời giải:
a) Ta thấy 1,04 >1 và 1,7 < 2.
Do đó 1,041,7 < 1,042.
b) Ta thấy và
Do đó .
c) Ta có: 1,20,3 > 1,20 >1 (do 1,2 > 1 và 0,3 > 0)
Và 0,91,8 < 0,90 < 1 (do 0 < 0,9 < 1 và 1,8 > 0)
Do đó 1,20,3 > 1 > 0,91,8.
d) Ta có: 30,4 > 30 = 1 (do 3 > 1 và 0,4 > 0);
3– 0,2 < 30 =1 (do 3 > 1 và – 0,2 < 0).
Do đó, ta có: 30,4 > 1> 3–0,2 hay > 1 > 30,2.
Bài 5 trang 18 SBT Toán 11 Tập 2: So sánh các cặp số sau:
Lời giải:
Bài 6 trang 18 SBT Toán 11 Tập 2: So sánh các cặp số sau:
a) log 4,9 và log 5,2;
b) log0,3 0,7 và log0,3 0,8;
c) và .
Lời giải:
a) Hàm số log x có cơ số là 10 > 1 nên đồng biến trên (0; +∞) và do 4,9 < 5,2.
Do đó log 4,9 < log 5,2;
b) Hàm số log0,3 x có cơ số 0 < 0,3 < 1 nên nghịch biến trên (0; +∞) và 0,7 < 0,8.
Do đó log0,3 0,7 > log0,3 0,8;
c) Hàm số log0,3 x có cơ số là 3 > 1 nên đồng biến trên (0; +∞) và π > 3.
Do đó (1)
Hàm số có cơ số là π > 1 nên đồng biến trên (0; +∞) và π > 3.
Do đó (2)
Kết hợp (1) và (2) ta có, < 1 < .
Vậy < .
Bài 7 trang 18 SBT Toán 11 Tập 2: So sánh các cặp số sau:
a) 2 log0,6 5 và ;
b) 6 log5 2 và 2 log5 6 ;
c) và ;
d) 2 log3 7 và 6 log9 4.
Lời giải:
a) Ta có 2 log0,6 5 = log0,6 52 = log0,6 25;
.
Do hàm số log0,6 x cơ số 0 < 0,6 < 1 nên hàm số nghịch biến trên (0; +∞) và 25 > 24 .
Do đó log0,6 25 < log0,6 24.
Vậy 2 log0,6 5 < .
b) Ta có 6 log5 2 = log5 26 = log5 64;
2 log5 6 = log5 62 = log5 36
Do hàm số log5 x cơ số 5 > 1 nên hàm số đồng biến trên (0; +∞) và 64 > 36.
Do đó log5 64 > log5 36,
Vậy 6 log5 2 > 2 log5 6;
c) Ta có ;
.
Do hàm số log2 x cơ số 2 > 1 nên hàm số đồng biến trên (0; +∞) và 11 < 12.
Do đó log2 11 < log2 12,
Vậy .
d) Ta có 2 log3 7 = log3 72 = log3 49;
=
= ;
Do hàm số log3 x cơ số 3 > 1 nên hàm số đồng biến trên (0; +∞) và 49 < 64.
Do đó log3 49 < log3 64.
Vậy 2 log3 7 < 6 log9 4.
Bài 8 trang 18 SBT Toán 11 Tập 2: Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = f(x) = trên đoạn [−1; 4];
b) y = f(x) = trên đoạn [−2; 2].
Lời giải:
Bài 9 trang 18 SBT Toán 11 Tập 2: Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = f(x) = trên đoạn ;
b) y = f(x) = log2 (x + 1) trên đoạn .
Lời giải:
a) Tại sao có thể khẳng định rằng 0 < a < 1?
b) Biết rằng bệnh nhân đã uống 100 mg thuốc và sau 1 giờ thì lượng thuốc trong cơ thể còn 80 mg. Hãy xác định giá trị của D0 và a.
c) Sau 5 giờ, lượng thuốc đã giảm đi bao nhiêu phần trăm so với lượng thuốc ban đầu?
Lời giải:
a) Do lượng thuốc trong cơ thể giảm dần, nên hàm số D(t) nghịch biến, do đó 0 < a < 1
b) Ta có: D0 = 100, 80 = 100.a1 (mg) ⇒ a = = 0,8.
Vậy D0 = 100, a = 0,8.
c) Sau 5 giờ, lượng thuốc đã còn còn D(5) = 100.0,85.
Tỉ lệ lượng thuốc đã giảm so với lượng thuốc ban đầu là
.
Vậy sau 5 giờ, lượng thuốc đã giảm đi khoảng 67,23% so với lượng thuốc ban đầu.
Xem thêm các bài giải SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Các quy tắc tính đạo hàm
Lý thuyết Hàm số mũ. Hàm số lôgarit
1. Hàm số mũ
- Hàm số được gọi là hàm số mũ cơ số a.
- Hàm số có:
+ Tập xác định: .
+ Tập giá trị: .
+ Hàm số liên tục trên .
+ Sự biến thiên:
+ Đồ thị:
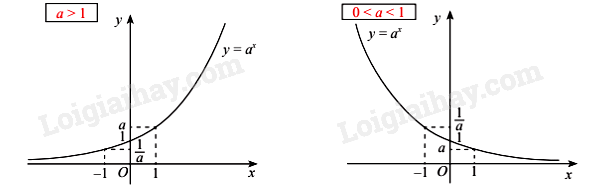
2. Hàm số lôgarit
- Hàm số được gọi là hàm số lôgarit cơ số a.
- Hàm số có:
+ Tập xác định: .
+ Tập giá trị: .
+ Hàm số liên tục trên .
+ Sự biến thiên:
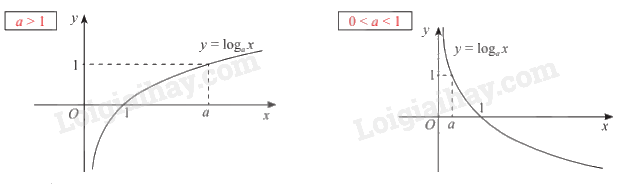
+ Đồ thị: