Với giải sách bài tập Toán 8 Bài 2: Đường trung bình của tam giác sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 2: Đường trung bình của tam giác
Lời giải:
a) Chứng minh tứ giác BMNC là hình thang.
b) Gọi E là trung điểm của BC và I là giao điểm của AE với MN. Chứng minh I là trung điểm của MN.
Lời giải
a) Xét ∆ABC, ta có MA = MB và NA = NC, nên MN là đường trung bình của ∆ABC.
Suy ra MN // BC.
Tứ giác BMNC có MN // BC nên BMNC là hình thang.
b) Xét ∆ABE, ta có MA = MB và MI // BE (vì I ∈ MN, E ∈ BC) nên IA = IE.
Do đó MI là đường trung bình của ∆ABE, suy ra MI = .
Tương tự, ta có IN = .
Mặt khác BE = EC, suy ra MI = IN.
Vậy I là trung điểm của MN.
a) EF = FB;
b) AE = AB;
c) CE = 4EI.
Lời giải:
a) Xét ∆BCE, ta có MB = MC và MF // CE nên EF = FB.
b) Xét ∆AMF, ta có IA = IM và EI // MF (vì I ∈ CE) nên EA = EF.
Suy ra EA = EF = FB mà EA + EF + FB = AB.
Vậy AE = AB.
c) Xét ∆BCE, ta có MB = MC và EF = FB, nên MF là đường trung bình của ∆BCE.
Suy ra CE = 2MF (1)
Tương tự, có EI là là đường trung bình của ∆AMF, suy ra MF = 2EI (2)
Từ (1) và (2) suy ra CE = 4EI.
a) MN // DE;
b) ND // ME.
Lời giải:
a) Xét ∆ABC, ta có MA = MC và NA = NB nên MN là đường trung bình của ∆ABC.
Suy ra MN // BC (1)
Xét ∆BCG, ta có BD = DG và CE = EG nên DE là đường trung bình của ∆BCG.
Suy ra DE // BC (2)
Từ (1) và (2) suy ra MN // DE.
b) Xét ∆ABG có NA = NB và DG = DB nên ND là đường trung bình của ∆ABG.
Suy ra ND // AG (3)
Xét ∆ACG có MA = MC và EG = EC nên ME là đường trung bình của ∆ACG.
Suy ra ME // AG (4)
Từ (3) và (4) suy ra ND // ME.
Lời giải:
• Xét ∆ABD, ta có MA = MD và PB = PD nên MP là đường trung bình của ∆ABD.
Suy ra MP //AB mà AB // CD nên MP // CD.
• Xét ∆ADC, ta có MA = MD và QA = QC nên MQ là đường trung bình của ∆ADC.
Suy ra MQ // CD.
• Xét ∆BCD, ta có PB = PD và NB = NC nên BN là đường trung bình của ∆BCD.
Suy ra PN // CD.
Qua điểm M ∉ CD có MP // CD và MQ // CD, suy ra M, P, Q thẳng hàng. (1)
Qua điểm P ∉ CD có MP // CD và PN // CD, suy ra M, P, N thẳng hàng. (2)
Từ (1) và (2) suy ra bốn điểm M, N, P, Q thẳng hàng.
a) Chứng minh tứ giác AMNB là hình thang.
b) Gọi I là giao điểm của AN và BM.Trên tia đối của tia NA lấy điểm E sao cho NE = NI. Trên tia đối của tia MB lấy điểm F sao cho ME = MI. Chứng minh EF // AB.
Lời giải:
a) Xét ∆ABC, ta có MA = MC và NB = NC nên MN là đường trung bình của ∆ABC.
Suy ra MN // AB (1)
Tứ giác AMNB có MN // AB nên AMNB là hình thang.
b) Xét ∆IEF, ta có NE = NI và MF = MI nên MN là đường trung bình của ∆IEF.
Suy ra MN // EF (2)
Từ (1) và (2) suy ra EF // AB.
a) Tam giác IMN cân tại I;
b) OI là đường trưng trực của MN.
Lời giải:
a) Xét ∆OPQ, ta có IP = IQ và IM // QO nên MO = MP.
Xét ∆OPQ, ta có IP = IQ và MO = MP nên IM là đường trung bình của ∆OPQ.
Suy ra IM = QO.
Tương tự, IN là đường trung bình của ∆OPQ, suy ra IN = PO.
Mà ∆OPQ cân tại O nên QO = PO. Suy ra IM = IN.
Tam giác IMN có IM = IN suy ra tam giác IMN cân tại I.
b) Gọi A là giao điểm của IO và MN.
∆OPQ cân tại O có OI là đường trung tuyến, suy ra OI cũng là đường cao của ∆OPQ.
Suy ra OI ⊥ PQ (1)
Xét ∆OPQ, ta có MO = MP và NO = NQ nên MN là đường trung bình của ∆OPQ.
Suy ra MN // PQ (2)
Từ (1) và (2) suy ra MN ⊥ OI tại A hay MN ⊥ IA.
Mà ∆IMN cân tại I có IA là đường cao nên IA cũng là đường trung trực của MN.
Do đó, OI là đường trung trực của MN.
Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Định lí Thalès trong tam giác
Bài 2: Đường trung bình của tam giác
Bài 3: Tính chất đường phân giác của tam giác
Bài 2: Các trường hợp đồng dạng của hai tam giác
Lý thuyết Đường trung bình của tam giác
1. Khái niệm
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Chú ý: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.
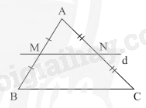
2. Tính chất
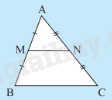
Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.