Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 2: Đường trung bình của tam giác chi tiết sách Toán 8 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 2: Đường trung bình của tam giác
Lời giải:
Xét tam giác ABC, ta có:
Theo định lí Thalès đảo, ta có DE // BC.
Suy ra , vậy BC = 2DE = 90 m.
Sau khi học xong bài này:
Ta có: D, E là trung điểm của AB và AC nên DE là đường trung bình của tam giác ABC
suy ra vậy BC = 2DE = 90 m.
1. Đường trung bình của tam giác
Lời giải:
Xét tam giác ABC có MN // BC, theo định lí Thalès, ta có:
Suy ra N là trung điểm của AC.
Thực hành 1 trang 52 Toán 8 Tập 2: Tìm độ dài đoạn thẳng NQ trong Hình 4.
Lời giải:
Ta có: mà hai góc này ở vị trí đồng vị nên MN // PQ.
Xét tam giác OPQ ta có:
MN // PQ
M là trung điểm OP
Suy ra MN là đường trung bình tam giác OPQ.
Do đó là trung điểm OQ ⇒ NQ = ON = 4.
Vận dụng 1 trang 53 Toán 8 Tập 2: Trong Hình 5, chứng minh MN là đường trung bình của tam giác ABC.
Lời giải:
Ta có: MN ⊥ AB, AC ⊥ AB nên MN // AC.
Xét tam giác ABC có:
MN // AC
M là trung điểm AB
Suy ra MN là đường trung bình tam giác ABC.
2. Tính chất của đường trung bình
a) Tính các tỉ số ;
b) Chứng minh MN // BC;
c) Chứng minh
Lời giải:
a) Vì M là trung điểm AB suy ra
Tương tự,
b) Xét tam giác ABC có
Theo định lí Thalès đảo, ta có: MN // BC.
c) Xét tam giác ABC có MN // BC.
Áp dụng hệ quả định lí Thalès, ta có:
Lời giải:
D là trung điểm của JK suy ra
E là trung điểm của JL suy ra JL = 2EL = 2.3,7 = 7,4 (cm)
Trong tam giác JKL có:
D là trung điểm của JK
E là trung điểm của JL
Suy ra DE là đường trung bình của tam giác JKL.
Do đó KL = 2DE = 2.6,5 = 13 (cm).
Vận dụng 2 trang 53 Toán 8 Tập 2: Hãy tính khoảng cách BC trong phần Hoạt động khởi động (trang 52).
Lời giải:
Xét tam giác ABC ta có:
Theo định lí Thalès đảo ta có DE // BC.
Suy ra , vậy BC = 2DE = 90 m.
Ta có: D là trung điểm của AB
E là trung điểm của AC
Suy ra DE là đường trung bình của tam giác ABC.
⇒
Vậy BC = 2DE = 90 m.
Bài tập
Lời giải:
a) Xét tam giác ABC có MN là đường trung bình ta có:
BC = 2MN
x = 12.
b) Xét tam giác ABC có MN là đường trung bình ta có:
BC = 2MN
2x + 3 = 14
x = 112.
c) Xét tam giác ABC có MN là đường trung bình ta có:
BC = 2MN
58 = 2(5x − 1)
58 = 10x – 2
x = 6
Bài 2 trang 54 Toán 8 Tập 2: Tính độ dài đoạn PQ (Hình 10).
Lời giải:
Xét tam giác ABC có:
AP = PB = 8 cm
AQ = QC = 7 cm
Khi đó, PQ là đường trung bình tam giác ABC.
Do đó (cm).
Lời giải:
Ta có: ;
;
.
Xét tam giác ABC có:
P là trung điểm của BC
Q lần lượt là trung điểm của AC
Do đó PQ là đường trung bình tam giác ABC.
Khi đó
Tương tự: ;
Vậy , , , , , .
a) Tam giác FBA và tam giác FCK có bằng nhau không? Vì sao?
b) Chứng minh EF // CD // AB.
c) Chứng minh
Lời giải:
a) Xét tam giác FBA và FCK ta có:
(hai góc đối đỉnh)
FB = FC (giả thiết)
(AB // CD, hai góc so le trong)
Do đó ΔFBA = ΔFCK (g.c.g)
b) ΔFBA = ΔFCK suy ra FA = FK
Xét tam giác ADK có:
EA = ED
FA = FK
Do đó, EF là đường trng bình tam giác ABC.
Suy ra EF // DK
Mà AB // CD nên EF // CD // AB.
c) EF là đường trung bình tam giác ADK.
Suy ra
Mà CK = BA (do ΔFBA = ΔFCK)
Do đó
Lời giải:
Xét tam giác ABC ta có:
M là trung điểm của AB (gt);
N là trung điểm của AC (gt);
Do đó MN là đường trung bình của tam giác ABC nên MN // BC.
Suy ra tứ giác MNPH là hình thang.
Xét tam giác ABC ta có:
M là trung điểm của AB (gt);
P là trung điểm của BC;
Do đó MP là đường trung bình của tam giác ABC nên MN=
Vì ΔACH vuông tại H có HN là trung tuyến (N là trung điểm của AC) nên NH=
Mà MP= (cmt) nên NH = MP.
Hình thang MNPH (MN // PH) có MP = NH nên là hình thang cân.
Bài 6 trang 54 Toán 8 Tập 2: Một mái nhà được vẽ lại như Hình 13. Tính độ dài x trong hình mái nhà.
Lời giải:
Xét tam giác ABH có:
AD = BD
BE = EH
Do đó DE là đường trung bình tam giác ABH nên
Khi đó
Lời giải:
Xét tam giác ADE có:
B là trung điểm AD
C là trung điểm AE
Do đó BC là đường trung bình của tam giác ADE.
Khi đó DE = 2BC = 2.232 = 464 (m).
Lý thuyết Đường trung bình của tam giác
1. Khái niệm
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Chú ý: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.
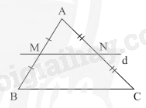
2. Tính chất
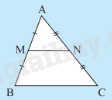
Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.