Với giải sách bài tập Toán 8 Bài 1: Hai tam giác đồng dạng sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 1: Hai tam giác đồng dạng
Lời giải:
Trên cạnh AB lấy điểm D sao cho .
Từ D kẻ đường thẳng song song với BC và cắt AC tại E.
Ta có ∆ADE ᔕ ∆ABC theo tỉ số đồng dạng .
Dựng ∆A’B’C’ = ∆ADE.
Dựng A’B’ = AD.
Dựng cung tròn tâm A’ bán kính AE và cung tròn tâm B’ bán kính DE, hai cung tròn cắt nhau tại C’.
Nối B’C’, A’C’ ta được tam giác phải dựng.
Ta có ∆ADE ᔕ ∆ABC theo tỉ số nên ∆A’B’C’ ᔕ ∆ABC theo tỉ số .
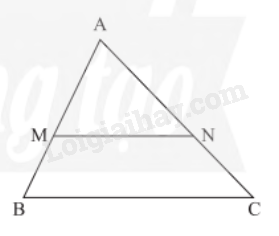
a) Chứng minh rằng ∆ADE ᔕ ∆AMN.
b) Tính tỉ số đồng dạng của ∆ADE và ∆AMN.
Lời giải:
a) Ta có MN là đường trung bình của tam giác ABC, suy ra MN // BC.
Suy ra ∆ABC ᔕ ∆AMN. Mà ∆ADE ᔕ ∆ABC, suy ra ∆ADE ᔕ ∆AMN.
b) ∆ADE ᔕ ∆ABC theo tỉ số .
∆ABC ᔕ ∆AMN theo tỉ số (vì M là trung điểm AB).
Suy ra hay .
Vậy ∆ADE ᔕ ∆AMN theo tỉ số .
Bài 3 trang 59 SBT Toán 8 Tập 2: Trong Hình 6, cho biết ∆ABC ᔕ ∆DEE.
a) Tính số đo .
b) Tính độ dài các đoạn thẳng AB và EF.
Lời giải:
a) Ta có ∆ABC ᔕ ∆DEE nên = 34°.
Vậy .
b) Ta có ∆ABC ᔕ ∆DEE suy ra
hay .
Suy ra và .
Do đó và .
Vậy AB = 2,8 và EF = 5,4.
a) ∆SUV ᔕ ∆SRT.
b) .
Lời giải:
a) Ta có UV // RT suy ra ∆SUV ᔕ ∆SRT.
b) Ta có (so le trong), (RV là tia phân giác ).
Suy ra nên ∆RUV cân tại U. Do đó UR = UV.
Mà (∆SUV ᔕ ∆SRT). Suy ra .
Bài 5 trang 59 SBT Toán 8 Tập 2: Trong Hình 8, cho biết tứ giác ABCD là hình bình hành. Tìm x.
Lời giải:
Ta có AE // DC (ABCD là hình bình hành).
Suy ra ∆IAE ᔕ ∆IDC, suy ra hay .
Khi đó x – 3 = 5,6, suy ra x = 5,6 + 3 = 8,6.
Vậy x = 8,6.
Lời giải:
• Vì ∆ABC ᔕ ∆DEF nên ta có
hay .
Suy ra và .
Do đó và .
• Vì ∆DEF ᔕ ∆IHK nên ta có
hay .
Suy ra và .
Do đó và .
Vậy AB = 2,8; EF = 5,4; IH = 6,3 và HK = 8,1.
a) Chứng mình rằng ∆IDA ᔕ ∆IBC.
b) Tính khoảng cách BC.
Lời giải:
a) Ta có AD // BC, suy ra ∆IDA ᔕ ∆IBC.
b) Ta có ∆IDA ᔕ ∆IBC, suy ra hay .
Suy ra (m).
Vậy BC = 51 m.
Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Các trường hợp đồng dạng của hai tam giác
Bài 3: Các trường hợp đồng dạng của hai tam giác vuông
Lý thuyết Hai tam giác đồng dạng
1. Khái niệm
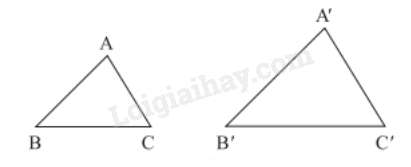
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
và
Kí hiệu: (viết theo thứ tự cặp đỉnh tương ứng).
Tỉ số là tỉ số đồng dạng của với .
2. Tính chất
Tính chất 1. Mỗi tam giác đồng dạng với chính nó theo tỉ số k = 1.
Tính chất 2. Nếu theo tỉ số k thì theo tỉ số .
Ta nói và đồng dạng với nhau.
Tính chất 3.
3. Định lí
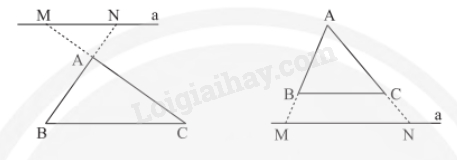
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Chú ý: Định lí trên cũng đúng trong trường hợp đường thẳng a cắt phần kéo dài của hai cạnh và song song với cạnh còn lại.