Sách bài tập Toán 8 Bài 2 (Chân trời sáng tạo): Các trường hợp đồng dạng của hai tam giác

Admin Vietjack Ngày: 23-09-2024 Lớp 8

1.9 K

Với giải sách bài tập Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác

Trường hợp đồng dạng thứ nhất (c.c.c)

Bài 1 trang 62 SBT Toán 8 Tập 2: Tam giác ABC có độ dài AB = 9 cm, AC = 12 cm, BC = 14 cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 61.25 cm. Hãy tính độ dài các cạnh của tam giác A'B'C'.

Lời giải:

Ta có ∆A’B’C’ ᔕ ∆ABC, suy ra

$\frac{A' B'}{A B} = \frac{A' C'}{A C} = \frac{B' C'}{B C}$ hay $\frac{A' B'}{9} = \frac{A' C'}{12} = \frac{B' C'}{14}$

Áp dụng tính chất tỉ lệ thức, có:

$\frac{A' B'}{9} = \frac{A' C'}{12} = \frac{B' C'}{14}$ = $\frac{A' B' + A' C' + B' C'}{9 + 12 + 14} = \frac{61, 25}{35} = \frac{7}{4}$ .

Suy ra $\frac{A' B'}{9} = \frac{7}{4}$ ; $\frac{A' C'}{12} = \frac{7}{4}$ và $\frac{B' C'}{14} = \frac{7}{4}$ .

Do đó $A' B' = \frac{7.9}{4} = 15, 75$ ; $A' C' = \frac{7.12}{4} = 21$ và $B' C' = \frac{7.14}{4} = 24, 5$ .

Vậy A’B’ = 15,75 cm ; A’C’ = 21 cm và B’C’ = 24,5 cm.

Bài 2 trang 62 SBT Toán 8 Tập 2: a) Tam giác ABC và MBN (Hình 4) có đồng dạng với nhau không? Vì sao?

b) Biết tam giác ABC có chu vi bằng 15 cm. Tính chu vi tam giác MBN.

Tam giác ABC và MBN (Hình 4) có đồng dạng với nhau không?

Lời giải:

a) Ta có AB = AM + MB = x + 2x = 3x.

Ta lại có $\frac{M B}{A B} = \frac{x}{3 x} = \frac{1}{3}$ ; $\frac{M N}{A C} = \frac{y}{3 y} = \frac{1}{3}$ và $\frac{N B}{B C} = \frac{z}{3 z} = \frac{1}{3}$ .

Xét ∆MBN và ∆ABC có: $\frac{M B}{A B} = \frac{M N}{A C} = \frac{N B}{B C}$ .

Suy ra ∆MBN ᔕ ∆ABC (c.c.c).

b) Ta có MBN ᔕ ∆ABC.

Khi đó, tỉ số chu vi của hai tam giác bằng tỉ số đồng dạng là:

$\frac{P_{M B N}}{P_{A B C}} = \frac{1}{3}$ hay $\frac{P_{M B N}}{15} = \frac{1}{3}$ .

Do đó $P_{M B N} = \frac{1.15}{3} = 5$ .

Vậy chu vi tam giác MBN là 5 cm.

Bài 3 trang 63 SBT Toán 8 Tập 2: Cho tam giác MAB và ABN như Hình 5. Biết MA = 10 cm, MB = 15 cm, AB = 8 cm, NA = 12 cm, NB = 6,4 cm. Chứng minh rằng:

a) ∆MAB ᔕ ∆ABN.

b) Tứ giác AMBN là hình thang.

Cho tam giác MAB và ABN như Hình 5. Biết MA = 10 cm, MB = 15 cm, AB = 8 cm

Lời giải:

a) Ta có $\frac{M A}{A B} = \frac{10}{8} = \frac{5}{4}$ ; $\frac{A B}{B N} = \frac{8}{6, 4} = \frac{5}{4}$ ; $\frac{M B}{A N} = \frac{15}{12} = \frac{5}{4}$ .

Xét ∆MAB và ∆ABN có $\frac{M A}{A B} = \frac{A B}{B N} = \frac{M B}{A N}$ .

Do đó ∆MAB ᔕ ∆ABN (c.c.c).

b) Ta có ∆MAB ᔕ ∆ABN, suy ra $\hat{M A B} = \hat{N B A}$ .

Mà $\hat{M A B}$ và $\hat{N B A}$ là hai góc so le trong, suy ra MA // BN.

Suy ra tứ giác AMBN là hình thang.

Bài 4 trang 63 SBT Toán 8 Tập 2: Anh Minh dự định thiết kế sân vườn nhà mình có hai bồn hoa hình tam giác đồng dạng với nhau (Hình 6). Bồn hoa thứ nhất có chu vi 7,5 m và cạnh dài nhất là 3,5 m. Bồn hoa thứ hai có chu vi 4,5 m. Tính độ dài cạnh dài nhất của bồn hoa thứ hai.

Anh Minh dự định thiết kế sân vườn nhà mình có hai bồn hoa hình tam giác đồng dạng

Lời giải:

Ta có ∆ABC ᔕ ∆DEF, suy ra $\frac{B C}{E F} = \frac{P_{Δ A B C}}{P_{Δ D E F}} = \frac{7, 5}{4, 5} = \frac{5}{3}$ .

Suy ra $\frac{3, 5}{E F} = \frac{5}{3}$ , suy ra $E F = \frac{3.3, 5}{5} = 2, 1$ (m).

Vậy độ dài cạnh dài nhất của bồn hoa thứ hai là 2,1 m.

Trường hợp đồng dạng thứ hai (c.g.c)

Bài 5 trang 63 SBT Toán 8 Tập 2: Quan sát Hình 7. Chứng minh rằng $\hat{O B A} = \hat{O A C}$ .

Quan sát Hình 7. Chứng minh rằng góc OBA = góc OAC

Lời giải:

Ta có $\frac{O B}{O A} = \frac{4}{6} = \frac{2}{3}$ ; $\frac{O A}{O C} = \frac{6}{9} = \frac{2}{3}$ , suy ra $\frac{O B}{O A} = \frac{O A}{O C}$ .

Xét ∆OAB và ∆OCA có $\frac{O B}{O A} = \frac{O A}{O C}$ và $\hat{O}$ chung.

Do đó ∆OAB ᔕ ∆OCA (c.g.c).

Suy ra $\hat{O B A} = \hat{O A C}$ (hai góc tương ứng).

Bài 6 trang 63 SBT Toán 8 Tập 2: Quan sát Hình 8.

a) Chứng minh rằng ∆ABC ᔕ ∆DEF.

b) Cho biết AM là đường trung tuyến của tam giác ABC, DN là đường trung tuyến của tam giác DEF và AM = 5,1 cm. Tính độ dài DN.

Quan sát Hình 8. a) Chứng minh rằng tam giác ABC đồng dạng am giác DEF

Lời giải:

a) Ta có $\frac{A B}{D E} = \frac{6}{8} = \frac{3}{4}$ ; $\frac{B C}{E F} = \frac{9}{12} = \frac{3}{4}$ , suy ra $\frac{A B}{D E} = \frac{B C}{E F}$ .

Xét ∆ABC và ∆DEF có

$\frac{A B}{D E} = \frac{B C}{E F}$ và $\hat{B} = \hat{E}$

Do đó ∆ABC ᔕ ∆DEF (c.g.c).

b) Ta có ∆ABC ᔕ ∆DEF nên

$\frac{A M}{D N} = \frac{A B}{D E} = \frac{3}{4}$ , suy ra $\frac{5, 1}{D N} = \frac{3}{4}$ .

Do đó $D N = \frac{4.5, 1}{3} = 6, 8$ .

Vậy DN = 6,8 cm.

Bài 7 trang 63 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho AM = 7,5 , AN = 6. Chứng minh rằng:

a) ∆ANM ᔕ ∆ABC.

b) $\hat{A B N} = \hat{A C M}$ .

Lời giải:

Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N

a) Xét ∆ANM và ∆ABC có

$\frac{A N}{A B} = \frac{A M}{A C} = \frac{1}{2}$ , $\hat{A}$ chung.

Do đó ∆ABC ᔕ ∆DEF (c.g.c).

b) Ta có $\frac{A N}{A B} = \frac{A M}{A C}$ , suy ra $\frac{A N}{A M} = \frac{A B}{A C}$ .

Xét ∆ANB và ∆AMC có

$\frac{A N}{A M} = \frac{A B}{A C}$ và $\hat{A}$ chung.

Do đó ∆ANB ᔕ ∆AMC (c.g.c).

Suy ra $\hat{A B N} = \hat{A C M}$ (hai góc tương ứng).

Bài 8 trang 64 SBT Toán 8 Tập 2: Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường này cắt nhau tại M. Qua M kẻ đường thẳng cắt AB tại E và cắt AC tại F. Chứng minh rằng:

a) $\frac{C A}{C F} = \frac{M E}{M F}$ và $\frac{B E}{B A} = \frac{M E}{M F}$ .

b) ∆BCE ᔕ ∆CFB.

Lời giải:

Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB

a) Xét ∆MCF có AE // CM (vì AB // CM), theo định lí Thalès ta có:

$\frac{C A}{C F} = \frac{M E}{M F}$ (1)

Xét ∆BEM có AF // BM (vì AC // BM), theo hệ quả của định lí Thalès ta có:

$\frac{A E}{B E} = \frac{E F}{M E}$ .

Ta có $\frac{A E}{B E} + 1 = \frac{E F}{M E} + 1$ hay $\frac{A E}{B E} + \frac{B E}{B E} = \frac{E F}{M E} + \frac{M E}{M E}$ .

Suy ra $\frac{B A}{B E} = \frac{M F}{M E}$ hay $\frac{B E}{B A} = \frac{M E}{M F}$ (2)

b) Từ (1) và (2), suy ra $\frac{C A}{C F} = \frac{B E}{B A}$ , mà AB = BC = AC. Suy ra $\frac{B C}{C F} = \frac{B E}{B C}$ .

Xét ∆BCE và ∆CFB có $\frac{B C}{C F} = \frac{B E}{B C}$ và $\hat{E B C} = \hat{B C F}$ (∆ABC đều).

Do đó ∆BCE ᔕ ∆CFB (c.g.c).

Trường hợp đồng dạng thứ ba (g.g)

Bài 9 trang 64 SBT Toán 8 Tập 2: Quan sát Hình 9.

a) Chứng minh rằng ∆ABC ᔕ ∆MNQ.

b) Tính x, y.

Quan sát Hình 9. a) Chứng minh rằng tam giác ABC đồng dạng tam giác MNQ

Lời giải:

a) Xét ∆ABC và ∆MNQ có

$\hat{A} = \hat{M}$ và $\hat{C} = \hat{Q}$

Do đó ∆ABC ᔕ ∆MNQ (g.g)

b) Ta có ∆ABC ᔕ ∆MNQ, suy ra

$\frac{A B}{M N} = \frac{A C}{M Q} = \frac{B C}{N Q}$ hay $\frac{y - 1}{5} = \frac{3, 5}{x + 2} = \frac{5}{10} = \frac{1}{2}$ .

Suy ra $\frac{y - 1}{5} = \frac{1}{2}$ và $\frac{3, 5}{x + 2} = \frac{1}{2}$ .

Do đó $y - 1 = \frac{5}{2} = 2, 5$ và x + 2 =7.

Suy ra y = 2,5 + 1 = 3,5 và x = 7 – 2 = 5.

Vây x = 5 và y = 3,5.

Bài 10 trang 64 SBT Toán 8 Tập 2: Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; $\hat{A B I}$ = 60°; $\hat{C D x}$ = 120°. Tính độ dài CD.

Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; góc ABI = 60 độ; góc CDx = 120 độ

Lời giải:

Ta có $\hat{C D x} + \hat{C D I} = 180 °$ (hai góc kề bù).

Suy ra $\hat{C D I} = 180 ° - \hat{C D I}$ = 180° - 120° = 60°.

Xét ∆IAB và ∆ICD có

$\hat{A B I} = \hat{C D I}$ (= 60°) và $\hat{A I B} = \hat{C I D}$ (đối đỉnh).

Suy ra ∆IAB ᔕ ∆ICD (g.g).

Suy ra $\frac{I A}{I C} = \frac{A B}{C D}$ hay $\frac{6}{10} = \frac{4, 2}{C D}$ .

Do đó $C D = \frac{4, 2.10}{6} = 7$ .

Vậy CD = 7.

Bài 11 trang 64 SBT Toán 8 Tập 2: Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với NP = 6 cm, $\hat{N} = 45 °$ , $\hat{P} = 75 °$ .

a) Chứng minh rằng ∆MNP ᔕ ∆ABC.

b) Dùng thước đo chiều dài cạnh MP của ∆MNP. Tính khoảng cách giữa hai điểm A và C ở hai bờ sông trong Hình 11.

Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với NP = 6 cm, góc N = 45 độ, góc P = 75 độ

Lời giải:

Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với NP = 6 cm, góc N = 45 độ, góc P = 75 độ

a) Xét ∆MNP và ∆ABC có

$\hat{N} = \hat{B}$ (= 45°) và $\hat{P} = \hat{C}$ (= 75°).

Do đó ∆MNP ᔕ ∆ABC (g.g).

b) Ta có MP = 4 cm.

Ta có ∆MNP ᔕ ∆ABC suy ra $\frac{M P}{A C} = \frac{N P}{B C}$ hay $\frac{4}{A C} = \frac{6}{36}$ .

Do đó $A C = \frac{4.36}{6} = 24$ .

Vậy AC = 24 cm.

Bài 12 trang 64 SBT Toán 8 Tập 2: Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của $\hat{A D C}$ và $\hat{D A B} = \hat{D B C}$ . Chứng minh rằng:

a) ∆ABD ᔕ ∆BDC.

b) BD² = AB . DC.

Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của

Lời giải:

a) Xét ∆ABD và ∆BDC có

$\hat{D A B} = \hat{D B C}$ và $\hat{A D B} = \hat{B D C}$ (DB là tia phân giác của $\hat{A D C}$ ).

Do đó ∆ABD ᔕ ∆BDC (g.g).

b) Ta có ∆ABD ᔕ ∆BDC, suy ra $\frac{A B}{B D} = \frac{B D}{D C}$ .

Do đó BD² = AB . DC (đpcm).

Bài 13 trang 65 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho $\hat{A D E} = \hat{A C B}$ .

a) Chứng minh rằng ∆AED ᔕ ∆ABC.

b) Tia phân giác của $\hat{B A C}$ cắt DE tại M và cắt BC tại N.

Chứng minh rằng ME . NC = MD . NB.

Lời giải:

Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E

a) Xét ∆AED và ∆ABC có

$\hat{A}$ chung; $\hat{A D E} = \hat{A C B}$ .

Do đó ∆AED ᔕ ∆ABC (g.g)

b) Ta có ∆AED ᔕ ∆ABC suy ra $\frac{A E}{A B} = \frac{A D}{A C}$ hay $\frac{A E}{A D} = \frac{A B}{A C}$ (1)

• Vì AM là tia phân giác của $\hat{D A E}$ nên $\frac{M E}{M D} = \frac{A E}{A D}$ (2)

• Vì AN là tia phân giác của $\hat{B A C}$ nên $\frac{N B}{N C} = \frac{A B}{A C}$ (3)

Từ (1); (2) và (3) suy ra $\frac{M E}{M D} = \frac{N B}{N C}$ hay ME . NC = MD . NB (đpcm).

Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8

Bài 1: Mô tả xác suất bằng tỉ số

Lý thuyết Các trường hợp đồng dạng của hai tam giác

1. Trường hợp đồng dạng thứ nhất (Cạnh – cạnh – cạnh)

Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

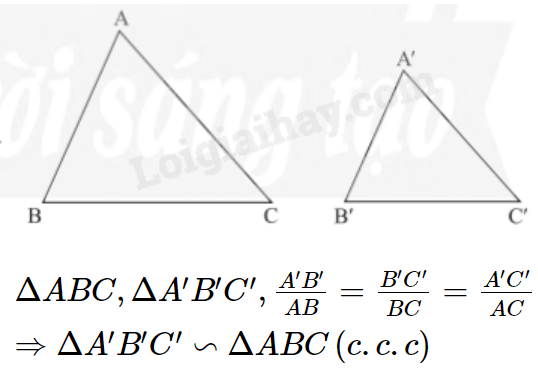
Lý thuyết Các trường hợp đồng dạng của hai tam giác (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

Nhận xét: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số chu vi của hai tam giác đó cũng bằng k.

2. Trường hợp đồng dạng thứ hai (cạnh – góc – cạnh)

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.

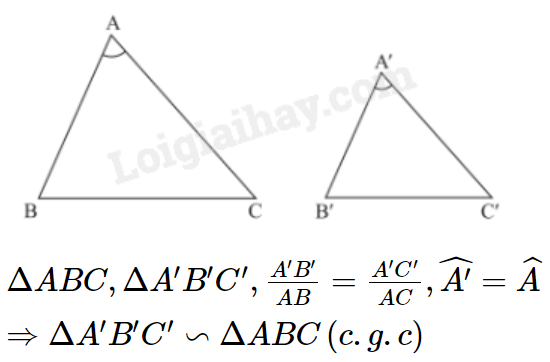
Lý thuyết Các trường hợp đồng dạng của hai tam giác (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 2)

Nhận xét: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số hai đường trung tuyến tương ứng của hai tam giác đó cũng bằng k.

3. Trường hợp đồng dạng thứ ba (góc – góc)

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

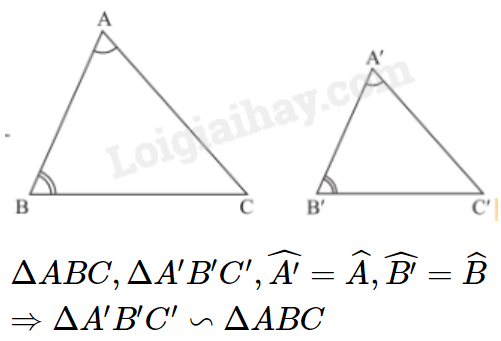
Lý thuyết Các trường hợp đồng dạng của hai tam giác (Chân trời sáng tạo 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 3)