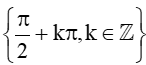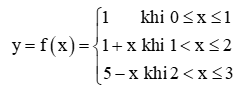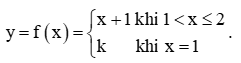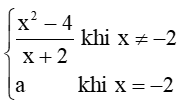Với lời giải Toán 11 trang 85 Tập 1 chi tiết trong Bài 3: Hàm số liên tục sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 Bài 3: Hàm số liên tục
Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:
a) f(x) = ;
b) g(x) = ;
c) h(x) = cosx + tanx.
Lời giải:
a) Tập xác định của hàm số D = ℝ \ {– 2; 2}.
Hàm số f(x) = liên tục tại mọi điểm khác – 2 và 2.
b) Tập xác định của hàm số D = [– 2; 2].
Hàm số g(x) = liên tục trên [– 2; 2].
c) Tập xác định của hàm số: D = R\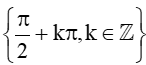 .
.
Hàm số y = cosx hoặc y = tanx đều liên tục trên các khoảng xác định của nó.
Vậy h(x) = cosx + tanx liên tục trên từng khoảng xác định.
Bài 4 trang 85 Toán 11 Tập 1: Cho hàm số f(x) = 2x – sinx, g(x) = . Xét tính liên tục của hàm số y = f(x).g(x) và y = .
Lời giải:
+) Xét hàm số y = f(x).g(x) có tập xác định D = [1; +∞).
Hàm số f(x) = 2x – sinx, g(x) = đều liên tục trên D.
Vậy hàm số y = f(x).g(x) liên tục trên D.
+) Xét hàm số y = có tập xác định D = (1; +∞).
Hàm số f(x) = 2x – sinx, g(x) = đều liên tục trên D.
Vậy hàm số y = liên tục trên D.
Bài 5 trang 85 Toán 11 Tập 1: Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau:
C(x) = 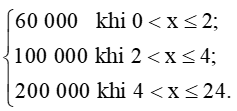
Xét tính liên tục của hàm số C(x).
Lời giải:
+) Với x ∈ (0; 2) ta có: C(x) = 60 000 nên hàm số liên tục trên (0; 2).
+) Với x ∈ (2; 4) ta có: C(x) = 100 000 nên hàm số liên tục trên (2; 4).
+) Với x ∈ (4; 24) ta có: C(x) = 200 000 nên hàm số liên tục trên (4; 24).
+) Tại x = 2 ta có: . Suy ra không tồn tại .
+) Tại x = 4 ta có: . Suy ra không tồn tại .
Bài 6 trang 85 Toán 11 Tập 1: Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là F(r) = 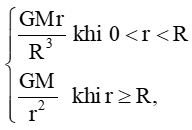 trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?
trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?
Lời giải:
+) Ta có: y = liên tục trên (0; R) và y = liên tục trên (R; + ∞).
+) Tại r = R, ta có:
Suy ra . Do đó
Mà nên
Suy ra hàm số liên tục tại x = R.
Vậy hàm số liên tục trên (0; +∞).
Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khởi động trang 80 Toán 11 Tập 1: Hai đồ thị ở hai hình dưới đây cho biết phí gửi xe y của ô tô con (tính theo 10 nghìn đồng) theo thời gian gửi x (tính theo giờ) của hai bãi xe. Có nhận xét gì về sự thay đổi của số tiền phí phải trả theo thời gian gửi ở mỗi bãi đỗ xe?...
Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số 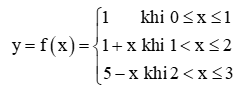 có đồ thị như Hình 1.....
có đồ thị như Hình 1.....
Thực hành 1 trang 81 Toán 11 Tập 1: Xét tính liên tục của hàm số:...
Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số 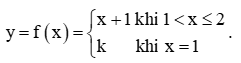 .....
.....
Thực hành 2 trang 82 Toán 11 Tập 1: Xét tính liên tục của hàm số: trên [1; 2]....
Vận dụng 1 trang 82 Toán 11 Tập 1: Tại một xưởng sản xuất bột đá thạch anh, giá bán (tính theo nghìn đồng) của x (kg) bột đá thạch anh được tính theo công thức sau:...
Hoạt động khám phá 3 trang 82 Toán 11 Tập 1: Cho hai hàm số y = f(x) = và y = g(x) = ....
Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số .....
Thực hành 4 trang 83 Toán 11 Tập 1: Cho hàm số f(x) = 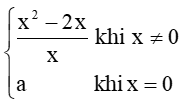 . Tìm a để hàm số y = f(x) liên tục trên ℝ.....
. Tìm a để hàm số y = f(x) liên tục trên ℝ.....
Vận dụng 2 trang 83 Toán 11 Tập 1: Một hãng taxi đưa ra giá cước T(x) (đồng) khi đi quãng đường x (km) cho loại xe 4 chỗ như sau:...
Hoạt động khám phá 4 trang 83 Toán 11 Tập 1: Cho hai hàm số y = f(x) = và y = g(x) = . Hàm số y = f(x) + g(x) có liên tục tại x = 2 không? Giải thích....
Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số:.....
Vận dụng 3 trang 84 Toán 11 Tập 1: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O, bán kính bằng 1. Một đường thẳng d thay đổi, luôn vuông góc với trục hoành, cắt trục hoành tại điểm M có hoành độ x (– 1 < x < 1) và cắt đường tròn (C) tại các điểm N và P (xem Hình 6)....
Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:....
Bài 2 trang 84 Toán 11 Tập 1: Cho hàm số f(x) = 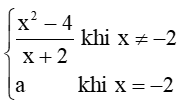 . Tìm a để hàm số f(x) liên tục trên ℝ....
. Tìm a để hàm số f(x) liên tục trên ℝ....
Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:...
Bài 4 trang 85 Toán 11 Tập 1: Cho hàm số f(x) = 2x – sinx, g(x) = . Xét tính liên tục của hàm số y = f(x).g(x) và y = ....
Bài 5 trang 85 Toán 11 Tập 1: Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau:..
Bài 6 trang 85 Toán 11 Tập 1: Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là F(r) = 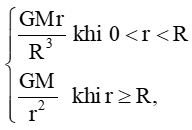 trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?....
trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?....
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Giới hạn của hàm số
Bài 3: Hàm số liên tục
Bài tập cuối chương 3