Với lời giải Toán 11 trang 83 Tập 1 chi tiết trong Bài 3: Hàm số liên tục sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 Bài 3: Hàm số liên tục
Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số .
Lời giải:
Đặt y = f(x) =
Tập xác định của hàm số D = (– ∞; 2) ∪ (2; +∞).
Với x0 ∈ ( – ∞; 2) thì
Suy ra hàm số liên tục trên ( – ∞; 2).
Với x0 ∈ ( 2; +∞) thì
Suy ra hàm số liên tục trên (2; +∞).
Thực hành 4 trang 83 Toán 11 Tập 1: Cho hàm số f(x) = 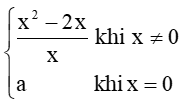
Lời giải:
+) Với x ≠ 0 thì f(x) = liên tục trên (– ∞; 0) và (0; + ∞).
+) Với x = 0 thì
Ta có: và f(0) = a.
Để y = f(x) liên tục trên ℝ thì f(x) phải liên tục tại x = 0 do đó a = – 2.
T(x) =
Xét tính liên tục của hàm số T(x).
Lời giải:
+) Với x0 ∈ (0; 0,7) hàm số f(x) = 10 000 là hàm đa thức nên liên tục trên (0; 0,7).
+) Với x0 ∈ (0,7; 20) hàm số f(x) = 10 000 + (x – 0,7).14 000 là hàm đa thức nên liên tục trên (0,7; 20).
+) Với x0 ∈ (20; +∞) hàm số f(x) = 280 200 + (x – 20).12 000 là hàm đa thức nên liên tục trên (20; +∞).
+) Tại x0 = 0,7 ta có:
;
[10 000 + (x-0,7).14 000] = 10 000.
Suy ra . Do đó tồn tại .
Mà f(0,7) = 10 000 nên = f(0,7) = 10000.
Vì vậy hàm số liên tục tại x0 = 0,7.
+) Tại x0 = 20 ta có:
[10 000 + (x-0,7).14 000] = 280 200.
[280 200+(x-20).12 000] = 280 200.
Suy ra . Do đó tồn tại .
Mà f(20) = 280 200 nên .
Vì vậy hàm số liên tục tại x = 20.
Vậy hàm số T(x) liên tục trên ℝ.
4. Tổng, hiệu, tích, thương của hàm số liên tục
Lời giải:
Xét hàm số y = h(x) = f(x) + g(x) = có tập xác định D = [4; +∞) \ {1}.
Tại x0 = 2 ∈ D thì = 3 = h(2).
Do đó hàm số liên tục tại x0 = 2.
Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số 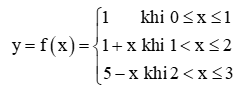
Thực hành 1 trang 81 Toán 11 Tập 1: Xét tính liên tục của hàm số:...
Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số 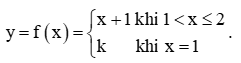
Thực hành 2 trang 82 Toán 11 Tập 1: Xét tính liên tục của hàm số: trên [1; 2]....
Hoạt động khám phá 3 trang 82 Toán 11 Tập 1: Cho hai hàm số y = f(x) = và y = g(x) = ....
Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số .....
Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số:.....
Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:....
Bài 2 trang 84 Toán 11 Tập 1: Cho hàm số f(x) = 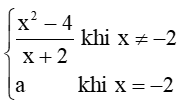
Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:...
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: