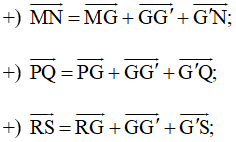Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S theo thứ tự là trung điểm của các cạnh AB, BC, CD, DE, EF, FA

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S theo thứ tự là trung điểm của các cạnh AB, BC, CD, DE, EF, FA

Nguyễn Thị Thuỳ Linh Ngày: 21-11-2022 Lớp 10

2.5 K

Với giải Bài 4.17 trang 54 SBT Toán lớp 10 Kết nối tri thức chi tiết trong Bài 9: Tích của một vectơ với một số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải sách bài tập Toán lớp 10 Bài 9: Tích của một vectơ với một số

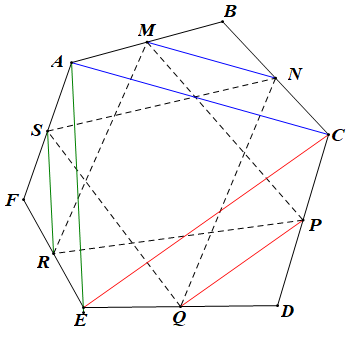
Bài 4.17 trang 54 SBT Toán 10 Tập 1: Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S theo thứ tự là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Lời giải:

+) Vì M, N lần lượt là trung điểm của AB, BC

Nên MN là đường trung bình của tam giác ABC.

Þ MN // AC và $M N = \frac{1}{2} A C$ (tính chất đường trung bình)

Do đó $\vec{M N} = \frac{1}{2} \vec{A C}$ (1)

Chứng minh tương tự ta cũng có: $\vec{P Q} = \frac{1}{2} \vec{C E}$ (2)

Và $\vec{R S} = \frac{1}{2} \vec{E A}$ (3)

Từ (1), (2) và (3) ta có:

$\vec{M N} + \vec{P Q} + \vec{R S} = \frac{1}{2} \vec{A C} + \frac{1}{2} \vec{C E} + \frac{1}{2} \vec{E A}$

$= \frac{1}{2} (\vec{A C} + \vec{C E} + \vec{E A})$

$= \frac{1}{2} (\vec{A E} + \vec{E A})$ (quy tắc ba điểm)

$= \frac{1}{2} \vec{AA}$ (quy tắc ba điểm)

$= \frac{1}{2} . \vec{0} = \vec{0}$

Do đó $\vec{M N} + \vec{P Q} + \vec{R S} = \vec{0}$

+) Giả sử G và G' lần lượt là trọng tâm của tam giác MPR và tam giác NQS.

Khi đó ta có: $\vec{M G} + \vec{P G} + \vec{R G} = \vec{0}$ và $\vec{N G^{'}} + \vec{Q G^{'}} + \vec{S G^{'}} = \vec{0}$ hay $\vec{G^{'} N} + \vec{G^{'} Q} + \vec{G^{'} S} = \vec{0}$

Mặt khác: theo quy tắc ba điểm ta có:

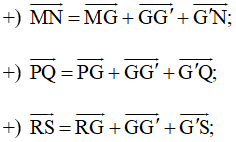
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

$\Rightarrow \vec{M N} + \vec{P Q} + \vec{R S} = \vec{M G} + \vec{P G} + \vec{R G} + 3. \vec{G G^{'}} + \vec{G^{'} N} + \vec{G^{'} Q} + \vec{G^{'} S}$

$= (\vec{M G} + \vec{P G} + \vec{R G}) + 3. \vec{G G^{'}} + (\vec{G^{'} N} + \vec{G^{'} Q} + \vec{G^{'} S})$

$= \vec{0} + 3. \vec{G G^{'}} + \vec{0}$

$= 3. \vec{G G^{'}}$

+) Lại có $\vec{M N} + \vec{P Q} + \vec{R S} = \vec{0}$ (chứng minh trên)

Nên $3 \vec{G G^{'}} = \vec{0}$

$\Rightarrow \vec{G G^{'}} = \vec{0}$

Suy ra G và G' trùng nhau.

Vậy hai tam giác MPR và NQS có cùng trọng tâm.

Xem thêm các bài giải sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 4.13 trang 54 SBT Toán 10 Tập 1: Cho tam giác ABC. Gọi D, E tương ứng là trung điểm của BC, CA. Hãy biểu thị các vectơ $\vec{A B}, \vec{B C}, \vec{C A}$ theo hai vectơ $\vec{A D}$ và $\vec{B E}$ ...

Bài 4.14 trang 54 SBT Toán 10 Tập 1: Cho tam giác OAB vuông cân, với OA = OB = a. Hãy xác định độ dài của các vectơ sau $\vec{O A} + \vec{O B},$ $\vec{O A} - \vec{O B},$ $\vec{O A} - \vec{O B},$ $2 \vec{O A} - 3 \vec{O B} .$ ..

Bài 4.15 trang 54 SBT Toán 10 Tập 1: Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O...

Bài 4.16 trang 54 SBT Toán 10 Tập 1: Cho tứ giác ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD và gọi I là trung điểm của MN. Chứng minh rằng với điểm O bất kì đều có...

Bài 4.18 trang 54 SBT Toán 10 Tập 1: Cho tam giác ABC đều với trọng tâm O. M là một điểm tuỳ ý nằm trong tam giác. Gọi D, E, F theo thứ tự là hình chiếu vuông góc của M trên BC, CA, AB...

Bài 4.19 trang 54 SBT Toán 10 Tập 1: Cho tam giác ABC...

Bài 4.20 trang 55 SBT Toán 10 Tập 1: Cho tam giác ABC...

Bài 4.21 trang 55 SBT Toán 10 Tập 1: Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực của vật và lực đẩy Archimedes mà chất lỏng tác động lên vật. Tính tỉ số giữa trọng lượng riêng của vật và của chất lỏng...

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vectơ với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Từ khóa :

toán 10 Giải sách bài tập Tích của một vecto với một số

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

170

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

143

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

117

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.