Với giải sách bài tập Toán 10 Bài tập cuối chương 3 sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài tập cuối chương 3
Giải SBT Toán 10 trang 40 Tập 1
A. Trắc nghiệm
Bài 3.17 trang 40 SBT Toán 10 Tập 1: Tam giác ABC có Giá trị của tanC bằng
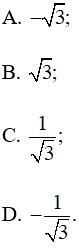
Lời giải:
Đáp án đúng là: A
Xét tam giác ABC ta có:
Do đó tanC = tan120° =
Ta chọn phương án A.
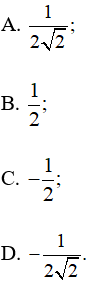
Lời giải:
Đáp án đúng là: C
Ta có
và
Mà xM = và yM =
Do đó xM.yM =
Ta chọn phương án C.
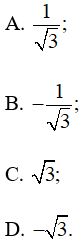
Lời giải:
Đáp án đúng là: A
Vì N đối xứng với M qua trục tung nên ta có:
• xN = –xM
Þ cos = –cos
Þ cos = –cos150°
Þ cos =
• yN = yM
sin = sin
sin = sin150°
sin =
• Ta có: tan =
Ta chọn phương án A.
Bài 3.20 trang 40 SBT Toán 10 Tập 1: Cho góc nhọn α có tanα = Giá trị của tích sinα.cosα bằng
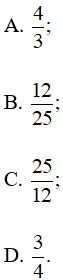
Lời giải:
Đáp án đúng là: B
Ta có: tanα =
Do đó sinα.cosα = cosα.cosα = cos2α.
Mặt khác tanα =
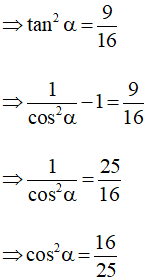
Do đó sinα.cosα =
Ta chọn phương án B.
A. 0;
B. 1;
C. –1;
D. Không tồn tại.
Lời giải:
Đáp án đúng là: A
Ta có: sinα + cosα = 1.
(sinα + cosα)2 = 12.
sin2α + 2.sinα.cosα + cos2α = 1.
(sin2α + cos2α) + 2.sinα.cosα = 1.
1 + 2.sinα.cosα = 1.
2.sinα.cosα = 0.
sinα.cosα = 0.
cosα = 0
(Vì 0° < α < 180° nên sinα > 0)
cotα =
Ta chọn phương án A.
Bài 3.22 trang 40 SBT Toán 10 Tập 1: Cho góc α thỏa mãn sinα + cosα = Giá trị của tanα + cotα là
A. 1;
B. –2;
C. 0;
D. 2.
Lời giải:
Đáp án đúng là: D
Ta có: sinα + cosα =
(sinα + cosα)2 = 2
sin2α + 2.sinα.cosα + cos2α = 2
(sin2α + cos2α) + 2.sinα.cosα = 2
1 + 2.sinα.cosα = 2
2.sinα.cosα = 1
sinα.cosα =
tanα + cotα =
Ta chọn phương án D.
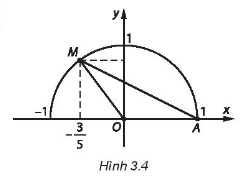
Diện tích của tam giác AOM bằng
Lời giải:
Đáp án đúng là: B
Gọi h là độ dài đường cao kẻ từ M đến OA của tam giác OAM.
Khi đó h = yM = sin
Mà sin2 + cos2 = 1
sin2 = 1 –
sin2 =
sin2 =
Mà Þ sin > 0
Do đó sin =
Ta có:
Ta chọn phương án B.
Giải SBT Toán 10 trang 41 Tập 1
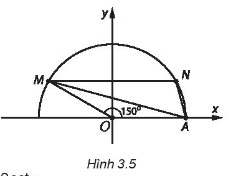
Lấy N đối xứng với M qua trục tung. Diện tích của tam giác MAN bằng
Lời giải:
Đáp án đúng là: A
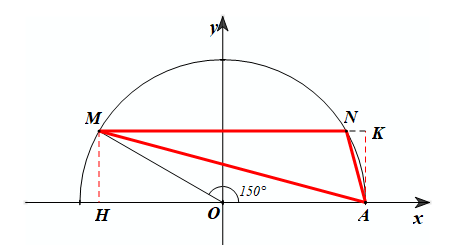
Gọi H và K lần lượt là chân đường vuông góc kẻ từ M đến Ox và kẻ từ A đến MN.
Ta có: SDAMN =
Mà N đối xứng với M qua trục tung Oy nên ta có:
xN = –xM nên |xM| = |xN|
MN = |xM| + |xN| = 2|xM| =
MN = |2cos150°| =
Lại có AK = MH = |yM| = |sin| = |sin150°|
AK =
Vậy SDAMN
Ta chọn phương án A.
Bài 3.25 trang 41 SBT Toán 10 Tập 1: Cho cosα = Giá trị của là
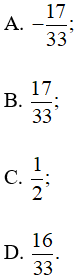
Lời giải:
Đáp án đúng là: B
Ta có cosα = Þ cos2α =
Mà
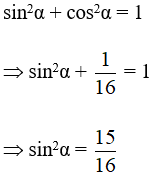
Ta có:
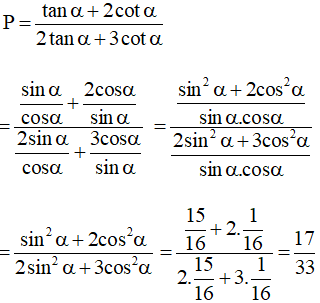
Ta chọn phương án B.
Lời giải:
Đáp án đúng là: D
Tam giác ABC có a = 2, b = 3, c = 4 nên:
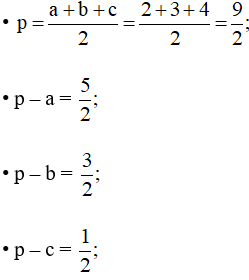
Áp dụng công thức Heron ta có:
Mà
Ta chọn phương án D.
Bài 3.27 trang 41 SBT Toán 10 Tập 1: Tam giác ABC có a = 4, b = 5, c = 6. Độ dài đường cao hb bằng
Lời giải:
Đáp án đúng là: A
Tam giác ABC có a = 4, b = 5, c = 6 nên:
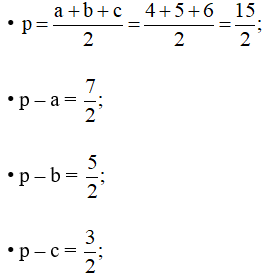
Áp dụng công thức Heron ta có:
Mà
Ta chọn phương án A.
A. 92;
B. 100;
C. 96;
D. 88.
Lời giải:
Đáp án đúng là: C
Áp dụng công thức tính độ dài đường trung tuyến cho tam giác ABC ta có:
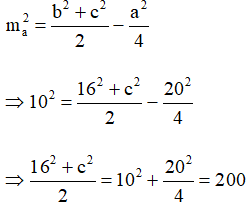
162 + c2 = 400
c2 = 144
c = 12.
Tam giác ABC có a = 20, b = 16, c = 12 nên:
•
• p – a = 4;
• p – b = 8;
• p – c = 12.
Áp dụng công thức Heron ta có:
Ta chọn phương án C.
Lời giải:
Đáp án đúng là: A
Áp dụng công thức tính độ dài đường trung tuyến cho tam giác ABC ta có:
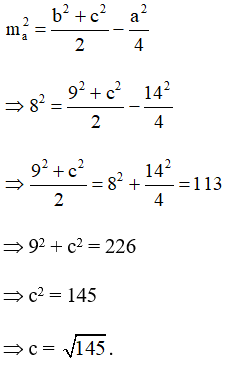
Tam giác ABC có a = 14, b = 9, c = nên:
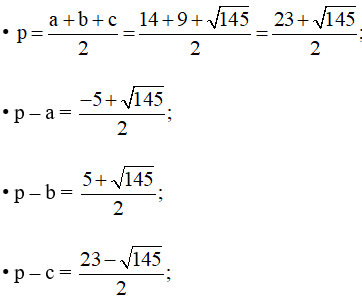
Áp dụng công thức Heron ta có:
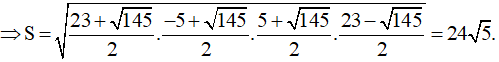
Mà:
Ta chọn phương án A.
Giải SBT Toán 10 trang 42 Tập 1
Bài 3.30 trang 42 SBT Toán 10 Tập 1: Tam giác ABC có c = 6, Độ dài đường cao hb bằng
Lời giải:
Đáp án đúng là: A
Xét tam giác ABC có:
Áp dụng định lí sin ta có:
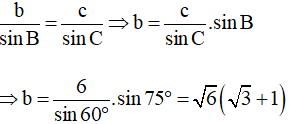
Áp dụng công thức tính diện tích tam giác ta có:
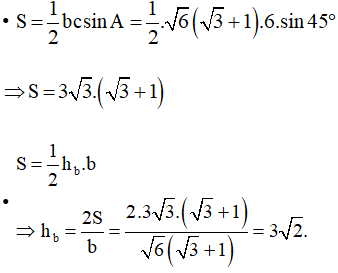
Ta chọn phương án A.
Lời giải:
Đáp án đúng là: B
Xét tam giác ABC có:
Áp dụng định lí sin ta có:
Ta chọn phương án B.
A. 60°;
B. 90°;
C. 30°;
D. 75º.
Lời giải:
Đáp án đúng là: B
Áp dụng định lí sin cho tam giác ABC ta có:
a = 2R.sinA; b = 2R.sinB và c = 2R.sinC.
Theo công thức tính diện tích tam giác ta có:
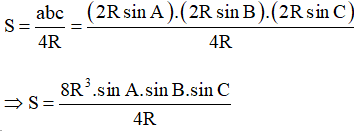
Þ S = 2R2.sin A.sinB.sinC.
Mà theo bài S = 2R2.sinB.sinC.
Do đó sinA = 1
Ta chọn phương án B.
Bài 3.33 trang 42 SBT Toán 10 Tập 1: Tam giác ABC có và Độ dài cạnh BC bằng
A. 3;
B. 2;
C.
D.
Lời giải:
Đáp án đúng là: B
Áp dụng định lí côsin cho tam giác ABC ta có:
AB2 = AC2 + BC2 – 2.AC.BC.cosC
= + BC2 – 2..BC
BC2 – BC – 3 = 0
BC = 2 (vì BC > 0)
Ta chọn phương án B.
Bài 3.34 trang 42 SBT Toán 10 Tập 1: Tam giác ABC có AC = 2 và Diện tích của tam giác ABC bằng
Lời giải:
Đáp án đúng là: C
Áp dụng định lí côsin cho tam giác ABC ta có:
AB2 = AC2 + BC2 – 2.AC.BC.cosC
= 22 + BC2 – 2..BC
BC2 – 2BC – 3 = 0
BC = 3 (vì BC > 0)
Áp dụng công thức tính diện tích tam giác ta có:
Ta chọn phương án C.
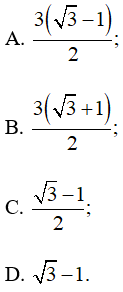
Lời giải:
Đáp án đúng là: A
Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
= 32 + AC2 – 2..AC
AC2 – 3AC – 18 = 0
AC = 6 (vì AC > 0)
Áp dụng công thức tính diện tích tam giác ta có:
Mà S = pr
Ta chọn phương án A.
Giải SBT Toán 10 trang 43 Tập 1
A. 110 km;
B. 112 km;
C. 111,4 km;
D. 110,5 km.
Lời giải:
Đáp án đúng là: C
Giả sử chuyển vị trí của cảng A, ca nô và tàu cá sau 2 giờ chuyển động được mô tả như hình vẽ sau:
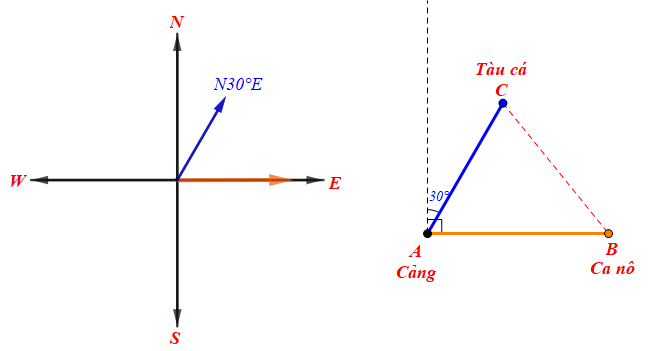
Vì ca nô chuyển động theo hướng đông và tàu cá chuyển động theo hướng N30°E nên ta có:
Sau 2 giờ ca nô chạy được quãng đường AB bằng:
2.60 = 120 (km)
Sau 2 giờ tàu cá chạy được quãng đường AC bằng:
2.50 = 100 (km)
Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos
BC2 = 1202 + 1002 – 2.120.100.cos60°
BC2 = 12 400
BC ≈ 111,4 (km).
Ta chọn phương án C.
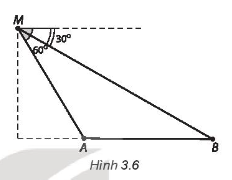
Khoảng cách giữa hai vận động viên A và B (làm tròn đến hàng đơn vị, theo đơn vị mét) tại thời điểm đó là
A. 8 m.
B. 7 m.
C. 6 m.
D. 9 m.
Lời giải:
Đáp án đúng là: B
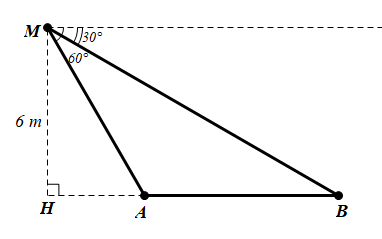
Gọi H là chân đài quan sát ở cuối đường đua.
Khi đó ta có:
• MH = 6 (m);
•
•
Tam giác AMH vuông tại H nên ta có:
HA = MH.tan = 6.tan30° =
Tam giác BMH vuông tại H nên ta có:
HB = MH.tan = 6.tan60°
Do đó AB = HB – HA = ≈ 7 (m).
Ta chọn phương án B.
B. Tự luận
Bài 3.38 trang 43 SBT Toán 10 Tập 1: Cho góc tù α có sinα =
a) Tính cosα, tanα, cotα.
b) Tính giá trị của các biểu thức:
A = sinα. cot(180° – α) + cos(180° – α).cot(90° – α);
Lời giải:
a) Vì α là góc tù (90° < α < 180°) nên cosα < 0.
Ta có sin2α + cos2α = 1
+ cos2α = 1
cos2α =
cosα = (do cosα < 0)
Do đó:
• tanα
• cotα =
Vậy cosα = tanα = và cotα =
b) Ta có:
• cot(180° – α) = –cotα;
• cos(180° – α) = –cosα;
• cot(90° – α) = tanα;
Khi đó:
A = sinα. cot(180° – α) + cos(180° – α).cot(90° – α)
= sinα.(–cotα) + (–cosα).tanα
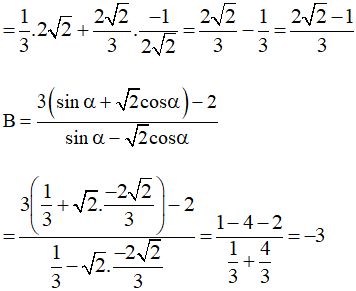
Vậy và B = –3.
Bài 3.39 trang 43 SBT Toán 10 Tập 1: Cho sin15° =
a) Tính sin75°, cos105°, tan165°.
b) Tính giá trị của biểu thức:
A = sin75°. cos165° + cos105°. sin165°.
Lời giải:
Vì 0° < 15° < 90° nên cos15° > 0.
Ta có sin215° + cos215° = 1
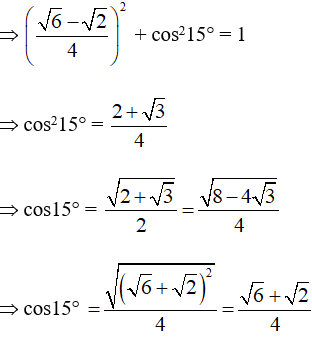
Do đó:
tan15° =
a) Ta có:
• sin75° = sin(90° – 15°) = cos15° =
• cos105° = cos(180° – 75°) = –cos75°
= –cos(90° – 15°) = –sin15°
Þ cos105° =
• tan165° = tan(180° – 15°) = –tan15°
Þ tan165° =
Vậy sin75° = cos105° = và tan165° =
b) Ta có:
• sin165° = sin(180° – 15°) = sin15°
Þ sin165° =
• cos165° = cos(180° – 15°) = –cos15°
Þ cos165° =
Khi đó:
A = sin75°. cos165° + cos105°. sin165°
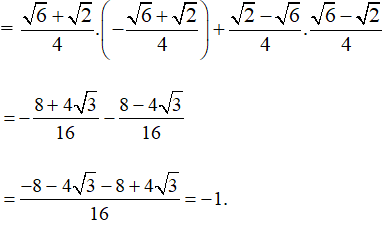
Vậy A = –1.
Lời giải:
Cách 1:
Áp dụng định lí côsin cho tam giác ABC ta có:
AC2 = AB2 + BC2 – 2.AB.BC.cos
AC2 = 12 + 22 – 2.1.2.cos60°
AC2 = 3
AC =
Áp dụng định lí sin cho tam giác ABC ta có:
và
và
Vậy và
Cách 2:
Tam giác ABC có AB = 1, BC = 2 nên
Mà
Do đó tam giác ABC vuông tại A
Suy ra
Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có:
AC2 = BC2 – AB2 = 22 – 12 = 3
AC =
Vậy và
Giải SBT Toán 10 trang 44 Tập 1
Bài 3.41 trang 44 SBT Toán 10 Tập 1: Cho tam giác ABC có c = 1, a = 2 và
a) Tính b,
b) Tính diện tích của tam giác.
c) Tính độ dài đường cao kẻ từ B của tam giác.
Lời giải:
a) Áp dụng định lí côsin cho tam giác ABC ta có:
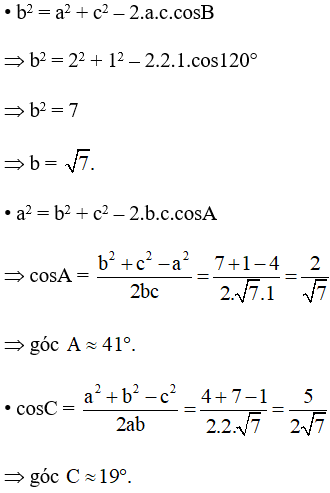
Vậy b = và
b) Áp dụng công thức tính diện tích tam giác ta có:
Vậy diện tích của tam giác ABC bằng
c) Áp dụng công thức tính diện tích tam giác ta có:
Vậy độ dài đường cao kẻ từ B của tam giác bằng
Bài 3.42 trang 44 SBT Toán 10 Tập 1: Cho tam giác ABC có a = 3, b = 5 và c = 7.
a) Tính các góc của tam giác, làm tròn đến độ.
b) Tính bán kính đường tròn nội tiếp và đường tròn ngoại tiếp của tam giác.
Lời giải:
a) Áp dụng định lí côsin cho tam giác ABC ta có:
• a2 = b2 + c2 – 2.b.c.cosA
cosA =
• b2 = a2 + c2 – 2.a.c.cosB
cosB =
• c2 = a2 + b2 – 2.a.b.cosC
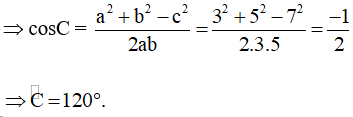
Vậy và
b) Tam giác ABC có a = 3, b = 5 và c = 7 nên:
Áp dụng công thức tính diện tích tam giác ta có:
•
• S = pr
•
Vậy bán kính đường tròn nội tiếp và ngoại tiếp của tam giác ABC lần luợt bằng và
Bài 3.43 trang 44 SBT Toán 10 Tập 1: Cho tam giác ABC có và Tính a, ha.
Lời giải:
Tam giác ABC có
Áp dụng định lí sin cho tam giác ABC ta có:
Áp dụng công thức tính diện tích tam giác ABC ta có:
•
•
Vậy và
Bài 3.44 trang 44 SBT Toán 10 Tập 1: Cho tam giác ABC có c = 5, a = 8 và
a) Tính b và số đo các góc A, C (số đo các góc làm tròn đến hàng đơn vị, theo đơn vị độ).
b) Tính độ dài đường cao kẻ từ B.
c) Tính độ dài trung tuyến kẻ từ A.
Lời giải:
a) Áp dụng định lí côsin cho tam giác ABC ta có:
• b2 = a2 + c2 – 2.a.c.cosB
b2 = 82 + 52 – 2.8.5.cos60°
b2 = 49
b = 7.
• a2 = b2 + c2 – 2.b.c.cosA
cosA =
• c2 = a2 + b2 – 2.a.b.cosC
cosC =
Vậy b = 7, và
b) Áp dụng công thức tính diện tích tam giác ABC ta có:
•
•
Vậy độ dài đường cao kẻ từ B của tam giác ABC bằng
c) Áp dụng công thức tính độ dài đường trung tuyến của tam giác ta có:
Vậy độ dài đường trung tuyến kẻ từ A của tam giác ABC là
Bài 3.45 trang 44 SBT Toán 10 Tập 1: Cho tam giác ABC có và c = 2.
a) Tính số đo góc A và độ dài các cạnh a, b.
b) Tính diện tích và bán kính đường tròn ngoại tiếp của tam giác.
c) Lấy điểm D thuộc cạnh AB sao cho (tức CD là phân giác của góc ). Tính độ dài CD.
Lời giải:
a) Xét tam giác ABC có:
Áp dụng định lí sin cho tam giác ABC ta có:
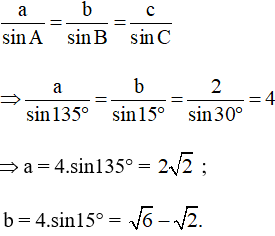
Vậy và b =
b) Áp dụng công thức tính diện tích tam giác ABC ta có:
•
•
Vậy diện tích và bán kính đường tròn ngoại tiếp của tam giác ABC lần lượt là và R = 2.
c)
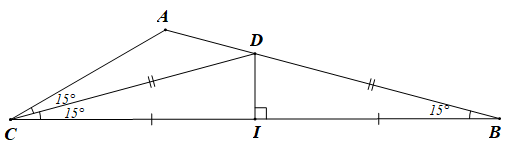
Vì CD là tia phân giác của nên
Mà
Do đó tam giác BCD cân tại D.
Gọi I là trung điểm của BC, khi đó DI là đường trung tuyến đồng thời là đường cao
IB = IC = và DI ⊥ BC.
Xét tam giác CDI vuông tại I ta có:
CD =
Vậy CD =
a) Tính khoảng cách từ A tới C (làm tròn đến hàng đơn vị, theo đơn vị kilômét).
b) Xác định hướng từ A tới C (làm tròn đến hàng đơn vị, theo đơn vị độ).
Lời giải:
Giả sử các vị trí cảng A, B và đảo C được mô tả như hình vẽ dưới đây:
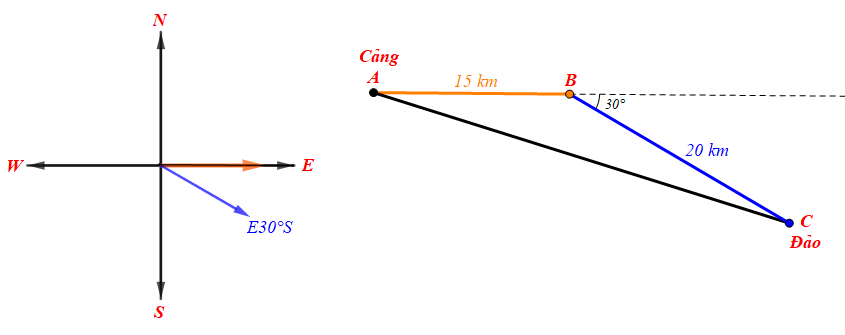
a) Do tàu cá xuất phát từ cảng A, chạy theo hướng đông tới B, rồi chuyển sang hướng E30°S chạy tiếp tới đảo C nên ta có:
Áp dụng định lí côsin ta có:
AC2 = AB2 + BC2 – 2.AB.BC.cos
Þ AC2 = 152 + 202 – 2.15.20.cos150°
Þ AC2 = 625 + 300
Þ AC ≈ 34 (km).
b) Áp dụng định lí sin cho tam giác ABC ta được:
Vậy hướng từ A đến C là E17°S.
Lời giải:
Giả sử người quan sát từ điểm A cách gốc cây B một khoảng 30m, nhìn ngọn cây C dưới góc 45° như hình vẽ dưới đây:
Do sườn đồi có độ dốc 12% (độ dốc của sườn đồi được tính bằng tang của góc nhọn tạo bởi sườn đồi với phương nằm ngang) nên tan = 12% = 0,12.
Do đó và
Áp dụng định lí sin cho tam giác ABC ta có:
Vậy chiều cao của cây đó khoảng 26 m.
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 6: Hệ thức lượng trong tam giác
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vectơ với một số