Với lời giải SBT Toán 10 trang 42 Tập 1 chi tiết trong Bài tập cuối chương 3 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 3

Bài 3.30 trang 42 SBT Toán 10 Tập 1:

Tam giác ABC có $\widehat{A}=45°,$ c = 6, $\widehat{B}=75°,$ Độ dài đường cao h_b bằng

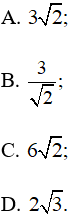
Lời giải:

Đáp án đúng là: A

Xét tam giác ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$

$$\begin{gathered} \Rightarrow \widehat{C}=180°-\widehat{A}-\widehat{B} \\ =180°-45°-75°=60° \end{gathered}$$

Áp dụng định lí sin ta có:

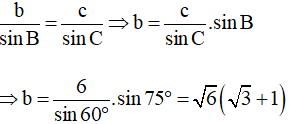
Áp dụng công thức tính diện tích tam giác ta có:

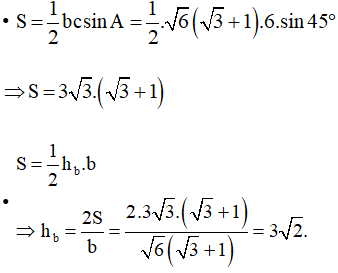
Ta chọn phương án A.

Bài 3.31 trang 42 SBT Toán 10 Tập 1:

Tam giác ABC có $\widehat{A}=45°,$ c = 6, $\widehat{B}=75°.$ Độ dài bán kính đường tròn ngoại tiếp của tam giác bằng

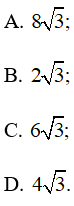
Lời giải:

Đáp án đúng là: B

Xét tam giác ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$

$$\begin{gathered} \Rightarrow \widehat{C}=180°-\widehat{A}-\widehat{B} \\ =180°-45°-75°=60° \end{gathered}$$

Áp dụng định lí sin ta có:

$$\begin{gathered} \frac{c}{\sin C}=2R \\ \Rightarrow R=\frac{c}{2\sin C}=\frac{6}{2.\sin 60°} \end{gathered}$$

$\Rightarrow R=\frac{6}{2.\frac{\sqrt{3}}{2}}=2\sqrt{3}.$

Ta chọn phương án B.

Bài 3.32 trang 42 SBT Toán 10 Tập 1:

Tam giác ABC có diện tích S = 2R². sin B.sinC, với R là độ dài bán kính đường tròn ngoại tiếp của tam giác. Số đo góc A bằng

A. 60°;

B. 90°;

C. 30°;

D. 75º.

Lời giải:

Đáp án đúng là: B

Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$

$\Rightarrow$ a = 2R.sinA; b = 2R.sinB và c = 2R.sinC.

Theo công thức tính diện tích tam giác ta có:

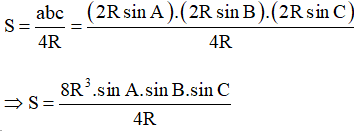
Þ S = 2R².sin A.sinB.sinC.

Mà theo bài S = 2R².sinB.sinC.

Do đó sinA = 1

$\Rightarrow \widehat{A}=90°.$

Ta chọn phương án B.

Bài 3.33 trang 42 SBT Toán 10 Tập 1:

Tam giác ABC có $AB=\sqrt{5},$ $AC=\sqrt{2}$ và $\widehat{C}=45°.$ Độ dài cạnh BC bằng

A. 3;

B. 2;

C. $\sqrt{3}$

D. $\sqrt{2}$

Lời giải:

Đáp án đúng là: B

Áp dụng định lí côsin cho tam giác ABC ta có:

AB² = AC² + BC² – 2.AC.BC.cosC

$\Rightarrow$ ${\left(\sqrt{5}\right)}^2$ = ${\left(\sqrt{2}\right)}^2$ + BC² – 2.$\sqrt{2}.\frac{\sqrt{2}}{2}$.BC

$\Rightarrow$ BC² – $\frac{1}{2}$BC – 3 = 0

$\Rightarrow$ BC = 2 (vì BC > 0)

Ta chọn phương án B.

Bài 3.34 trang 42 SBT Toán 10 Tập 1:

Tam giác ABC có $\widehat{C}=60°,$ AC = 2 và $AB=\sqrt{7}.$  Diện tích của tam giác ABC bằng

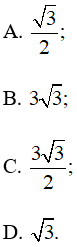
Lời giải:

Đáp án đúng là: C

Áp dụng định lí côsin cho tam giác ABC ta có:

AB² = AC² + BC² – 2.AC.BC.cosC

$\Rightarrow$ ${\left(\sqrt{7}\right)}^2$ = 2² + BC² – 2.$\frac{1}{2}$.BC

$\Rightarrow$ BC² – 2BC – 3 = 0

$\Rightarrow$ BC = 3 (vì BC > 0)

Áp dụng công thức tính diện tích tam giác ta có:

$S=\frac{1}{2}.AC.BC.\sin C=\frac{1}{2}\mathrm{.2.3.}\sin 60°=\frac{3\sqrt{3}}{2}.$

Ta chọn phương án C.

Bài 3.35 trang 42 SBT Toán 10 Tập 1:

Tam giác ABC có $\widehat{A}=60°,$ AB = 3 và $BC=3\sqrt{3}.$ Độ dài bán kính đường tròn nội tiếp của tam giác ABC là:

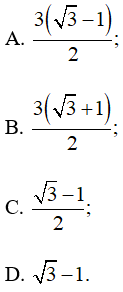
Lời giải:

Đáp án đúng là: A

Áp dụng định lí côsin cho tam giác ABC ta có:

BC² = AB² + AC² – 2.AB.AC.cosA

$\Rightarrow$ ${\left(3\sqrt{3}\right)}^2$ = 3² + AC² – 2.$\frac{1}{2}$.AC

$\Rightarrow$AC² – 3AC – 18 = 0

$\Rightarrow$ AC = 6 (vì AC > 0)

Áp dụng công thức tính diện tích tam giác ta có:

$$\begin{gathered} S=\frac{1}{2}.AB.AC.\sin A \\ =\frac{1}{2}\mathrm{.3.6.}\sin 60°=\frac{9\sqrt{3}}{2}. \end{gathered}$$

Mà S = pr $\Rightarrow r=\frac{S}{p}$

$\Rightarrow r=\frac{\frac{9\sqrt{3}}{2}}{\frac{3+6+3\sqrt{3}}{2}}=\frac{3\left(\sqrt{3}-1\right)}{2}$

Ta chọn phương án A.

Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 10 trang 40 Tập 1

Giải SBT Toán 10 trang 41 Tập 1

Giải SBT Toán 10 trang 43 Tập 1

Giải SBT Toán 10 trang 44 Tập 1

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 6: Hệ thức lượng trong tam giác

Bài tập cuối chương 3

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vectơ với một số