Với giải sách bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác

Giải SBT Toán 11 trang 14

Bài 1 trang 14 SBT Toán 11 Tập 1: Tính các giá trị lượng giác của góc α nếu:

a) $\sin \alpha =-\frac{4}{5}$ và $\pi <\alpha <\frac{3\pi }{2};$

b) $cos\alpha =\frac{11}{61}$ và $0<\alpha <\frac{\pi }{2};$

c) $\tan \alpha =-\frac{15}{8}$ và $-90°<\alpha <90°;$

d) cotα = ‒2,4 và ‒180° < α < 0°.

Lời giải:

a) Ta có ${\text{cos}}^2\alpha =1-{\text{sin}}^2\alpha =1-{\left(-\frac{4}{5}\right)}^2=\frac{9}{25}$. Vì $\pi <\alpha <\frac{3\pi }{2};$ nên cosα < 0.

Do đó $\text{cos}\alpha =-\frac{3}{5}.$

Suy ra $\text{tan}\alpha =\frac{\text{sin}\alpha }{\text{cos}\alpha }=\frac{-\frac{4}{5}}{-\frac{3}{5}}=\frac{4}{3}$ và $\text{cot}\alpha =\frac{1}{\text{tan}\alpha }=\frac{1}{\frac{4}{3}}=\frac{3}{4}.$

b) Ta có ${\text{sin}}^2\alpha =1-{\cos }^2\alpha =1-{\left(\frac{11}{61}\right)}^2={\left(\frac{60}{61}\right)}^2$ Vì $0<\alpha <\frac{\pi }{2};$ nên sinα > 0.

Do đó $\text{sin}\alpha =\frac{60}{61}.$

Suy ra $\text{tan}\alpha =\frac{\text{sin}\alpha }{\text{cos}\alpha }=\frac{\frac{60}{61}}{\frac{11}{61}}=\frac{60}{11}$ và $\text{cot}\alpha =\frac{1}{\text{tan}\alpha }=\frac{1}{\frac{60}{11}}=\frac{11}{60}.$

c) Ta có $\text{cot}\alpha =\frac{1}{\text{tan}\alpha }=\frac{1}{-\frac{15}{8}}=-\frac{8}{15};\frac{1}{{\text{cos}}^2\alpha }=1+{\text{tan}}^2\alpha =1+{\left(-\frac{15}{8}\right)}^2=\frac{289}{64}$

Suy ra ${\text{cos}}^2\alpha =\frac{64}{289}$. Vì $-90°<\alpha <90°;$ nên $\text{cos}\alpha >0$. Do đó $\text{cos}\alpha =\frac{8}{17}.$

Suy ra $\text{sin}\alpha =\text{tan}\alpha \text{cos}\alpha =-\frac{15}{8}\cdot \frac{8}{17}=-\frac{15}{17}.$

d) Ta có

 $$\begin{gathered} \text{tan}\alpha =\frac{1}{\text{cot}\alpha }=\frac{1}{-\mathrm{2,4}}=-\frac{5}{12}; \\ \frac{1}{{\text{sin}}^2\alpha }=1+{\text{cot}}^2\alpha =1+{\left(-\mathrm{2,4}\right)}^2=\frac{676}{100} \end{gathered}$$

Suy ra ${\text{sin}}^2\alpha =\frac{100}{676}$. Vì ‒180° < α < 0°  nên $\text{sin}\alpha <0$. Do đó $\text{sin}\alpha =-\frac{5}{13}.$

Suy ra $\text{cos}\alpha =\text{cot}\alpha \text{sin}\alpha =-\mathrm{2,4}\cdot \left(-\frac{5}{13}\right)=\frac{12}{13}.$

Bài 2 trang 14 SBT Toán 11 Tập 1: Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}$ (hoặc từ 0° đến 45°).

a) sin(‒1693°);

b) $cos\frac{1003\pi }{3};$

c) tan 885°;

d) $\cot \left(-\frac{53\pi }{10}\right).$

Lời giải:

a) sin(‒1693°) = ‒sin(1693°)

= ‒sin(4.360° + 180° + 73°)

= sin73°

= cos(90° ‒ 73°) = cos17°.

b) $\text{cos}\frac{1003\pi }{3}=\text{cos}\left(334\pi +\frac{\pi }{3}\right)=\text{cos}\frac{\pi }{3}=\text{sin}\frac{\pi }{6}$

c) tan 885° = tan(180.4 + 165°) = tan165° = tan(180° ‒ 15°) = ‒tan15°.

d) $\cot \left(-\frac{53\pi }{10}\right)=-\cot \left(\frac{53\pi }{10}\right)=-\cot \left(\frac{50\pi }{10}+\frac{3\pi }{10}\right)$

$=-\cot \left(5\pi +\frac{3\pi }{10}\right)=-\cot \left(\frac{3\pi }{10}\right)$

= $-\cot \left(\frac{\pi }{2}-\frac{\pi }{5}\right)=-\tan \left(\frac{\pi }{5}\right).$

Bài 3 trang 14 SBT Toán 11 Tập 1: Cho $\pi <\alpha <\frac{3\pi }{2}.$ Xác định dấu của các giá trị lượng giác sau:

a) cos(α + π);

b) $\sin \left(\frac{\pi }{2}-\alpha \right);$

c) $\tan \left(\alpha +\frac{3\pi }{2}\right);$

d) $\cot \left(\alpha -\frac{\pi }{2}\right);$

e) $\cos \left(2\alpha +\frac{\pi }{2}\right);$

g) sin(π ‒ 2α).

Lời giải:

Vì $\pi <\alpha <\frac{3\pi }{2}$  nên sinα < 0; cosα < 0, tanα > 0 và cotα > 0.

a) cos(α + π) = ‒cosα > 0 vì cosα < 0.

b) $\text{sin}\left(\frac{\pi }{2}-\alpha \right)=\text{cos}\alpha <0$ vì cosα < 0.

c) $\text{tan}\left(\alpha +\frac{3\pi }{2}\right)=-\text{cot}\alpha <0$ vì cotα > 0.

d) $\text{cot}\left(\alpha -\frac{\pi }{2}\right)=-\text{tan}\alpha <0$ vì tanα > 0.

e) Vì $\pi <\alpha <\frac{3\pi }{2}$  nên 2π < 2α < 3π, do đó sin2α > 0.

Vậy $\text{cos}\left(2\alpha +\frac{\pi }{2}\right)=-\text{sin}2\alpha <0$

g) sin (π ‒ 2α) = sin2α > 0 vì sin2α > 0.

Bài 4 trang 14 SBT Toán 11 Tập 1: Biết $\sin \alpha =\frac{3}{5}$ và $\frac{\pi }{2}<\alpha <\pi .$ Tính giá trị của các biểu thức sau:

a) $A=\frac{3\sin \alpha }{2cos\alpha -\tan \alpha };$

b) $B=\frac{{\cot }^2\alpha -\sin \alpha }{\tan \alpha +2cos\alpha }.$

Lời giải:

Vì $\frac{\pi }{2}<\alpha <\pi$  nên cosα < 0, tanα < 0 và cotα < 0.

Ta có: sin²α + cos²α = 1, suy ra ${\cos }^2\alpha =1-{\sin }^2\alpha =1-{\left(\frac{3}{5}\right)}^2=\frac{16}{25}$

Do đó $\cos \alpha =-\frac{4}{5}.$

Suy ra $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{\frac{3}{5}}{-\frac{4}{5}}=-\frac{3}{4}$  và $\cot \alpha =\frac{1}{\tan \alpha }=\frac{1}{-\frac{3}{4}}=-\frac{4}{3}.$

a) $A=\frac{3\cdot \frac{3}{5}}{2\cdot \left(-\frac{4}{5}\right)-\left(-\frac{3}{4}\right)}=\frac{\frac{9}{5}}{-\frac{8}{5}+\frac{3}{4}}=\frac{\frac{9}{5}}{-\frac{17}{20}}=-\frac{36}{17}.$

b) $B=\frac{{\left(-\frac{4}{3}\right)}^2-\frac{3}{5}}{-\frac{3}{4}+2\cdot \left(-\frac{4}{5}\right)}=\frac{\frac{16}{9}-\frac{3}{5}}{-\frac{3}{4}-\frac{8}{5}}=\frac{\frac{53}{45}}{-\frac{47}{20}}=-\frac{212}{423}.$

Bài 5 trang 14 SBT Toán 11 Tập 1: Chứng minh các đẳng thức lượng giác sau:

a) sin⁴x + cos⁴x = 1 ‒ 2sin²xcos²x.

b) $\frac{1+\cot x}{1-\cot x}=\frac{\tan x+1}{\tan x-1};$

c) $\frac{\sin \alpha +\cos \alpha }{{\sin }^3\alpha }=\frac{1-{\cot }^4\alpha }{1-\cot \alpha };$

d) $\frac{{\tan }^2\alpha +{\cos }^2\alpha -1}{{\cot }^2\alpha +{\sin }^2\alpha -1}={\tan }^6\alpha .$

Lời giải:

a)

 $$\begin{gathered} {\text{sin}}^{4}x+{\text{cos}}^{4}x={\left({\text{sin}}^{2}x+{\text{cos}}^{2}x\right)}^2-2{\text{sin}}^{2}x{\text{cos}}^{2}x \\ =1-2{\text{sin}}^{2}x{\text{cos}}^{2}x \end{gathered}$$;

b) $\frac{1+\text{cot}x}{1-\text{cot}x}=\frac{1+\frac{1}{\text{tan}x}}{1-\frac{1}{\text{tan}x}}=\frac{\frac{\text{tan}x+1}{\text{tan}x}}{\frac{\text{tan}x-1}{\text{tan}x}}=\frac{\text{tan}x+1}{\text{tan}x-1}.$

c)

 $$\begin{gathered} \frac{\text{sin}\alpha +\text{cos}\alpha }{{\text{sin}}^3\alpha }=\frac{1}{{\text{sin}}^2\alpha }+\frac{\text{cos}\alpha }{\text{sin}\alpha }\cdot \frac{1}{{\text{sin}}^2\alpha } \\ =\left(1+{\text{cot}}^2\alpha \right)+\text{cot}\alpha \left(1+{\text{cot}}^2\alpha \right) \end{gathered}$$

$=\left(1+\text{cot}\alpha \right)\left(1+{\text{cot}}^2\alpha \right)$

$=\frac{\left(1-{\text{cot}}^2\alpha \right)\left(1+{\text{cot}}^2\alpha \right)}{1-\text{cot}\alpha }=\frac{1-{\text{cot}}^4\alpha }{1-\text{cot}\alpha }$

d) $\frac{{\text{tan}}^2\alpha +{\text{cos}}^2\alpha -1}{{\text{cot}}^2\alpha +{\text{sin}}^2\alpha -1}=\frac{{\text{tan}}^2\alpha -{\text{sin}}^2\alpha }{{\text{cot}}^2\alpha -{\text{cos}}^2\alpha }=\frac{\frac{{\text{sin}}^2\alpha }{{\text{cos}}^2\alpha }-{\text{sin}}^2\alpha }{\frac{{\text{cos}}^2\alpha }{{\text{sin}}^2\alpha }-{\text{cos}}^2\alpha }$

$=\frac{{\text{sin}}^2\alpha \left(\frac{1}{{\text{cos}}^2\alpha }-1\right)}{{\text{cos}}^2\alpha \left(\frac{1}{{\text{sin}}^2\alpha }-1\right)}={\text{tan}}^2\alpha \cdot \frac{{\text{tan}}^2\alpha }{{\text{cot}}^2\alpha }={\text{tan}}^6\alpha$

Giải SBT Toán 11 trang 15

Bài 6 trang 15 SBT Toán 11 Tập 1: Chứng minh các đẳng thức sau:

a) ${\sin }^{2}605°+{\sin }^{2}1645°+{\cot }^{2}25°=\frac{1}{{\cos }^{2}65°};$

b) $\frac{\sin 530°}{1+\sin 640°}=\frac{1}{\sin 10°}+\cot 10°.$

Lời giải:

a) sin605° = sin(3.180° + 65°) = ‒sin65°.

sin1645° = sin(9.180° + 25°) = ‒sin25° = ‒sin(90° ‒ 65°) = ‒cos65°.

cot25° = cot(90° ‒ 65°) = tan65°.

sin²605° + sin²1645° + cot²25°

= (‒sin65°)² + (‒cos65°)² + (tan65°)²

= 1 + tan²65°

$=\frac{1}{{\text{cos}}^2{65}^{\circ }}$

b) sin530° = sin(3.180° ‒ 10°) = sin10°.

sin640° = sin(4.180° ‒ 80°) = sin(‒80°) = ‒sin80° = ‒sin(90° ‒ 10°) = ‒cos10°.

$\frac{\text{sin}530°}{1+\text{sin}640°}=\frac{\text{sin}10°}{1-\text{cos}10°}=\frac{{\text{sin}}^{2}10°}{\text{sin}10°\left(1-\text{cos}10°\right)}$

$=\frac{1-{\text{cos}}^{2}10°}{\text{sin}10°\left(1-\text{cos}10°\right)}=\frac{\left(1+\text{cos}10°\right)\left(1-\text{cos}10°\right)}{\text{sin}10°\left(1-\text{cos}10°\right)}$

$=\frac{1+\text{cos}10°}{\text{sin}10°}=\frac{1}{\text{sin}10°}+\text{cot}10°\text{ .}$

Bài 7 trang 15 SBT Toán 11 Tập 1: Rút gọn các biểu thức sau:

a) $\cos \left(\alpha +\pi \right)+\sin \left(\alpha +\frac{5\pi }{2}\right)-\tan \left(\alpha +\frac{\pi }{2}\right)\tan \left(\pi -\alpha \right).$

b) $\cos \left(\frac{\pi }{2}-\alpha \right)\sin \left(\beta +\pi \right)-\sin \left(2\pi -\alpha \right)\cos \left(\beta -\frac{\pi }{2}\right).$

Lời giải:

a) $\cos \left(\alpha +\pi \right)+\sin \left(\alpha +\frac{5\pi }{2}\right)-\tan \left(\alpha +\frac{\pi }{2}\right)\tan \left(\pi -\alpha \right)$

$=-\cos \alpha +\sin \left(\alpha +\frac{\pi }{2}\right)-\tan \left[\pi -\left(\alpha +\frac{\pi }{2}\right)\right]\tan \alpha$

$=-\cos \alpha +\sin \left[\pi -\left(\alpha +\frac{\pi }{2}\right)\right]-\tan \left(\frac{\pi }{2}-\alpha \right)\tan \alpha$

$=-\cos \alpha +\sin \left(\frac{\pi }{2}-\alpha \right)-\cot \alpha \tan \alpha$

$=-\cos \alpha +\cos \alpha -1=-1.$

b) $\cos \left(\frac{\pi }{2}-\alpha \right)\sin \left(\beta +\pi \right)-\sin \left(2\pi -\alpha \right)\cos \left(\beta -\frac{\pi }{2}\right)$

$=\sin \alpha \left(-\sin \beta \right)-\sin \left(-\alpha \right)\cos \left(\frac{\pi }{2}-\beta \right)$

$=-\sin \alpha \sin \beta +\sin \alpha \sin \beta =0.$

Bài 8 trang 15 SBT Toán 11 Tập 1: Tính giá trị của các biểu thức sau:

a) sin 17°sin197° + sin73°cos163°;

b) $\frac{1}{1-\tan 145°}+\frac{1}{1+\tan 55°}.$

Lời giải:

a) Ta có:

sin197° = sin(180° + 17°) = ‒sin17°.

sin73° = sin(90° ‒ 17°) = cos17°.

cos163° = cos(180° ‒ 17°) = ‒cos17°.

Suy ra:

sin 17°sin197° + sin73°cos163°

= sin 17°.(‒sin17°) + cos17°.(‒cos17°)

= ‒(sin²17° + cos²17°) = ‒1.

b) $\frac{1}{1-\text{tan}145°}+\frac{1}{1+\text{tan}55°}$

$=\frac{1}{1+\text{cot}55°}+\frac{1}{1+\text{tan}55°}$

$=\frac{1}{1+\frac{1}{\text{tan}55°}}+\frac{1}{1+\text{tan}55°}$

$=\frac{\text{tan}55°}{1+\text{tan}55°}+\frac{1}{1+\text{tan}55°}$

$=\frac{\text{tan}55°+1}{1+\text{tan}55°}=1$

Bài 9 trang 15 SBT Toán 11 Tập 1: a) Cho tanα + cotα = 2. Tính giá trị của biểu thức tan³α +cot³α.

b) Cho $\sin \alpha +\cos \alpha =\frac{1}{4}.$ Tính giá trị của sinαcosα.

c) Cho $\sin \alpha +\cos \alpha =\frac{1}{2}.$Tính giá tị của biểu thức sin³α + cos³α.

Lời giải:

a) tan³α + cot³α = (tanα + cotα)³ ‒ 3tanαcotα(tanα + cotα)

= (tanα + cotα)³ ‒ 3 (tanα + cotα)

= 2³ ‒ 3.2 = 2.

Thay tanα + cotα = 2 vào biểu thức (*) ta có: 2³ ‒ 3.2 = 2.

b) (sinα + cosα)² = sin²α + cos²α + 2 sinαcosα = 1 + 2 sinαcosα.

Do đó $\text{sin}\alpha \text{cos}\alpha =\frac{1}{2}\left[{(\text{sin}\alpha +\text{cos}\alpha )}^2-1\right]=\frac{1}{2}\left[{\left(\frac{1}{4}\right)}^2-1\right]=-\frac{15}{32}$

c) sin³α + cos³α

= (sinα + cosα)(sin²α ‒ sinαcosα + cos²α)

= (sinα + cosα)(1 ‒ sinαcosα)

Mà $\text{sin}\alpha \text{cos}\alpha =\frac{1}{2}\left[{(\text{sin}\alpha +\text{cos}\alpha )}^2-1\right]=\frac{1}{2}\left[{\left(\frac{1}{2}\right)}^2-1\right]=-\frac{3}{8}$, nên

${\text{sin}}^3\alpha +{\text{cos}}^3\alpha =\frac{1}{2}\cdot \left[1-\left(-\frac{3}{8}\right)\right]=\frac{1}{2}\cdot \frac{11}{8}=\frac{11}{16}$

Bài 10 trang 15 SBT Toán 11 Tập 1: Cho tanx = 2. Tính giá trị của các biểu thức sau:

a) $\frac{3\sin x-4\cos x}{5\sin x+2\cos x};$

b) $\frac{{\sin }^{3}x+2{\cos }^{3}x}{2\sin x+3\cos x}.$

Lời giải:

Vì tanx xác định nên cosx ≠ 0. Chia tử và mẫu của phân thức cho luỹ thừa thích hợp của cosx để biểu diễn biểu thức theo tanx.

a) $\frac{3\text{sin}x-4\text{cos}x}{5\text{sin}x+2\text{cos}x}=\frac{3\cdot \frac{\text{sin}x}{\text{cos}x}-4}{5\cdot \frac{\text{sin}x}{\text{cos}x}+2}$$=\frac{3\text{tan}x-4}{5\text{tan}x+2}=\frac{3.2-4}{5.2+2}=\frac{1}{6}$.

b) $\frac{{\text{sin}}^{3}x+2{\text{cos}}^{3}x}{2\text{sin}x+3\text{cos}x}=\frac{\frac{{\text{sin}}^{3}x}{{\text{cos}}^{3}x}+2}{\left(2\frac{\text{sin}x}{\text{cos}x}+3\right)\cdot \frac{1}{{\text{cos}}^{2}x}}=\frac{{\text{tan}}^{3}x+2}{\left(2\text{tan}x+3\right)\left({\text{tan}}^{2}x+1\right)}$

$=\frac{2^3+2}{\left(2\cdot 2+3\right)\left(2^2+1\right)}=\frac{2}{7}$

Bài 11 trang 15 SBT Toán 11 Tập 1: Độ dài của ngày từ lúc Mặt Trời mọc đến lúc Mặt Trời lặn ở một thành phố X trong ngày thứ t của năm được tính xấp xỉ bởi công thức:

$d\left(t\right)=4\sin \left[\frac{2\pi }{365}\left(t-80\right)\right]+12$ với t ∈ ℤ và 1 ≤ t ≤ 365.

Thành phố X vào ngày 31 tháng 1 có bao nhiêu giờ có Mặt Trời chiếu sáng? Làm tròn kết quả đến hàng phần mười.

Lời giải:

Thay t = 31 vào công thức trên ta có:

$d\left(31\right)=4\sin \left[\frac{2\pi }{365}\left(31-80\right)\right]+12\approx \mathrm{9,01}$ (giờ)

Vậy thành phố X vào ngày 31 tháng 1 có 9,01 giờ có Mặt Trời chiếu sáng.

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Góc lượng giác

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

Lý thuyết Giá trị lượng giác của một góc lượng giác

1. Giá trị lượng giác của góc lượng giác

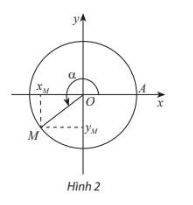
- Trên đường tròn, lấy điểm M(x;y) như hình vẽ. Khi đó:

$x=$cos$\alpha$, $y=$sin$\alpha$.

tan$\alpha$$=\frac{\sin \alpha }{\cos \alpha }=\frac{y}{x}\left(x\ne 0\right)$

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{x}{y}\left(y\ne 0\right)$

- Các giá trị sin$\alpha$, cos$\alpha$, tan$\alpha$, cot$\alpha$ được gọi là các giá trị lượng giác của góc lượng giác $\alpha$.

*Chú ý:

a, Trục tung là trục sin, trục hoành là trục côsin.

Trục As có gốc ở điểm A(1;0) và song song với trục sin là trục tang.

Trục Bt có gốc ở điểm B(0;1) và song song với trục coossin gọi là trục côtang.

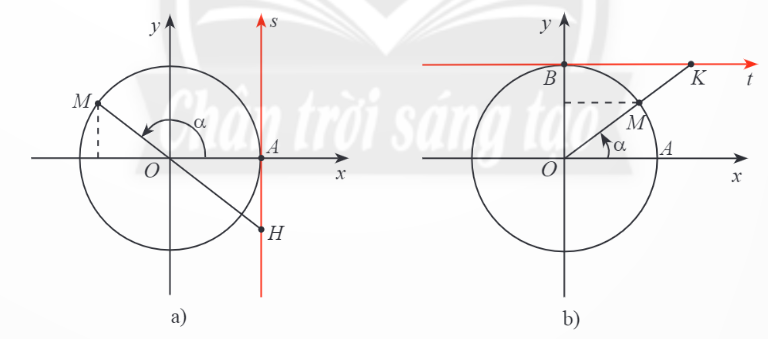
b, $\sin \alpha$và $\cos \alpha$ xác định với mọi $\alpha \in \mathbb{R}$.

$\tan \alpha$xác định với các góc  $\alpha \ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$.

$\cot \alpha$ xác định với các góc  $\alpha \ne k\pi ,k\in \mathbb{Z}$.

c, Với mọi góc lượng giác $\alpha$ và số nguyên k, ta có:

$\begin{array}{l}\sin \left(\alpha +k2\pi \right)=\sin \alpha \\ \cos \left(\alpha +k2\pi \right)=\cos \alpha \\ \tan \left(\alpha +k\pi \right)=\tan \alpha \\ \cot \left(\alpha +k\pi \right)=\cot \alpha \end{array}$

d, Bảng các giá trị lượng giác đặc biệt

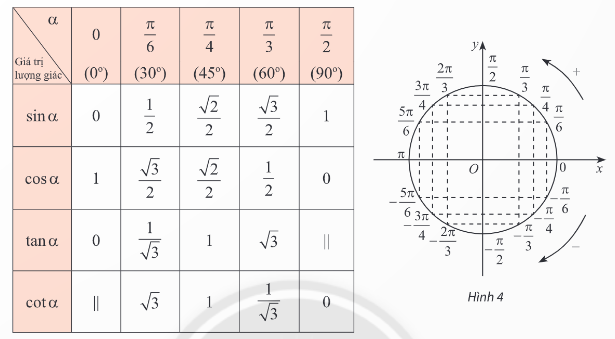
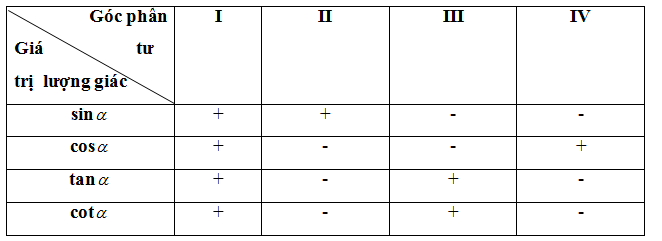
2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay

- Lần lượt ấn các phím SHIFT $\to$MENU $\to$2:

Để chọn đơn vị độ: ấn phím 1 (Degree).

Để chọn đơn vị radian: ấn phím 2 (Radian).

- Ấn các phím MENU 1 để vào chế độ tính toán.

3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác

$\begin{array}{l}{\sin }^2\alpha +{\cos }^2\alpha =1\\ 1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }\left(\alpha \ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right)\\ 1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }\left(\alpha \ne k\pi ,k\in \mathbb{Z}\right)\\ \tan \alpha .\cot \alpha =1\left(\alpha \ne \frac{k\pi }{2},k\in \mathbb{Z}\right)\end{array}$

4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt

• Hai góc đối nhau $\alpha$và $-\alpha$

$\begin{array}{l}\sin \left(-\alpha \right)=-\sin \alpha \\ \cos \left(-\alpha \right)=\cos \alpha \\ \tan \left(-\alpha \right)=-\tan \alpha \\ \cot \left(-\alpha \right)=-\cot \alpha \end{array}$

• Hai góc bù nhau ($\alpha$và $\pi$-$\alpha$)

$\begin{array}{l}\sin \left(\pi -\alpha \right)=\sin \alpha \\ \cos \left(\pi -\alpha \right)=-\cos \alpha \\ \tan \left(\pi -\alpha \right)=-\tan \alpha \\ \cot \left(\pi -\alpha \right)=-\cot \alpha \end{array}$

• Hai góc phụ nhau ($\alpha$và $\frac{\pi }{2}$-$\alpha$)

$\begin{array}{l}\sin \left(\frac{\pi }{2}-\alpha \right)=c\mathrm{o}\mathrm{s}\alpha \\ \cos \left(\frac{\pi }{2}-\alpha \right)=\sin \alpha \\ \tan \left(\frac{\pi }{2}-\alpha \right)=\cot \alpha \\ \cot \left(\frac{\pi }{2}-\alpha \right)=\tan \alpha \end{array}$

• Hai góc hơn kém $\pi$(và $\pi$+$\alpha$)

$\begin{array}{l}\sin \left(\pi +\alpha \right)=-\sin \alpha \\ \cos \left(\pi +\alpha \right)=-\cos \alpha \\ \tan \left(\pi +\alpha \right)=\tan \alpha \\ \cot \left(\pi +\alpha \right)=\cot \alpha \end{array}$