Với giải Bài 3 trang 14 SBT Toán lớp 11 Chân trời sáng tạo chi tiết trong Bài 2: Giá trị lượng giác của một góc lượng giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3 trang 14 SBT Toán 11 Tập 1: Cho $\pi <\alpha <\frac{3\pi }{2}.$ Xác định dấu của các giá trị lượng giác sau:

a) cos(α + π);

b) $\sin \left(\frac{\pi }{2}-\alpha \right);$

c) $\tan \left(\alpha +\frac{3\pi }{2}\right);$

d) $\cot \left(\alpha -\frac{\pi }{2}\right);$

e) $\cos \left(2\alpha +\frac{\pi }{2}\right);$

g) sin(π ‒ 2α).

Lời giải:

Vì $\pi <\alpha <\frac{3\pi }{2}$  nên sinα < 0; cosα < 0, tanα > 0 và cotα > 0.

a) cos(α + π) = ‒cosα > 0 vì cosα < 0.

b) $\text{sin}\left(\frac{\pi }{2}-\alpha \right)=\text{cos}\alpha <0$ vì cosα < 0.

c) $\text{tan}\left(\alpha +\frac{3\pi }{2}\right)=-\text{cot}\alpha <0$ vì cotα > 0.

d) $\text{cot}\left(\alpha -\frac{\pi }{2}\right)=-\text{tan}\alpha <0$ vì tanα > 0.

e) Vì $\pi <\alpha <\frac{3\pi }{2}$  nên 2π < 2α < 3π, do đó sin2α > 0.

Vậy $\text{cos}\left(2\alpha +\frac{\pi }{2}\right)=-\text{sin}2\alpha <0$

g) sin (π ‒ 2α) = sin2α > 0 vì sin2α > 0.

Giá trị lượng giác của góc lượng giác

a, Đường tròn lượng giác

Đường tròn lượng giác là đường tròn có tâm tại gốc tọa độ, bán kính bằng 1, được định hướng và lấy điểm A(1;0) làm điểm gốc của đường tròn.

Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo $\alpha$(độ hoặc rad) là điểm M trên đường tròn lượng giác sao cho sđ (OA, OM) =$\alpha$.

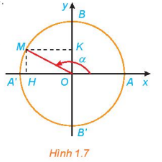
b, Các giá trị lượng giác của góc lượng giác:

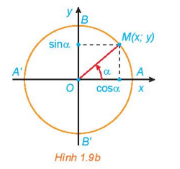
Trục tung là trục sin, trục hoành là trục côsin

Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:

$x=$cos$\alpha$, $y=$sin$\alpha$.

tan$\alpha$$=\frac{\sin \alpha }{\cos \alpha }=\frac{y}{x}\left(x\ne 0\right)$

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{x}{y}\left(y\ne 0\right)$.

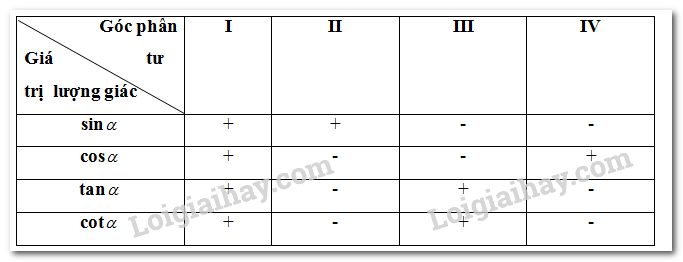
c, Bảng xác định dấu của các giá trị lượng giác

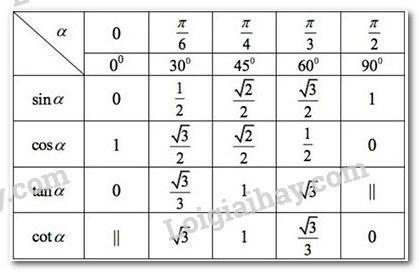
d, Giá trị lượng giác của các góc đặc biệt