Luyện tập 2 trang 17 Toán 7 Tập 1 | Kết nối tri thức Giải Toán lớp 7

Luyện tập 2 trang 17 Toán 7 Tập 1 | Kết nối tri thức Giải Toán lớp 7

Admin Vietjack Ngày: 25-08-2024 Lớp 7

3.1 K

Với giải Luyện tập 2 trang 17 Toán lớp 7 Kết nối tri thức với cuộc sống chi tiết trong Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ

Luyện tập 2 trang 17 Toán lớp 7: Tính:

$\begin{array}{l} a) {(\frac{2}{3})}^{10} {.3}^{10} \\ b) (- 125)^{3} {.25}^{3} \\ c) (0, 08)^{3} {.10}^{3} \end{array}$

Phương pháp giải:

$a^{n}$ = a.a….a (n thừa số a)

$\begin{array}{l} (x . y)^{n} = x^{n} . y^{n} \\ (\frac{x}{y})^{n} = \frac{x^{n}}{y^{n}} \end{array}$

Lời giải:

$\begin{array}{l} a) {(\frac{2}{3})}^{10} {.3}^{10} = \frac{2^{10}}{3^{10}} {.3}^{10} = 2^{10} \\ b) (- 125)^{3} : 25^{3} = (- 125 : 25)^{3} = (- 5)^{3} = - 125 \\ c) (0, 08)^{3} {.10}^{3} = (0, 08 . 10^{3} = (0, 8)^{3} = 0, 512 \end{array}$

Lý thuyết Lũy thừa với số mũ tự nhiên

• Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xⁿ, là tích của n thừa số x (n là số tự nhiên lớn hơn 1).

$x^{n} = \underset{n thừa số}{\underset{⏟}{x \cdot x \cdot x \cdot . .. \cdot x}}$ (x $\in ℚ$ , n $\in ℕ$ , n >1)

xⁿ đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.

x gọi là cơ số, n gọi là số mũ.

Quy ước: x⁰ = 1 (x ≠ 0); x¹ = x.

Ví dụ:

+ 5³ đọc là 5 mũ 3 hoặc 5 lũy thừa 3 hoặc lũy thừa bậc 3 của 5.

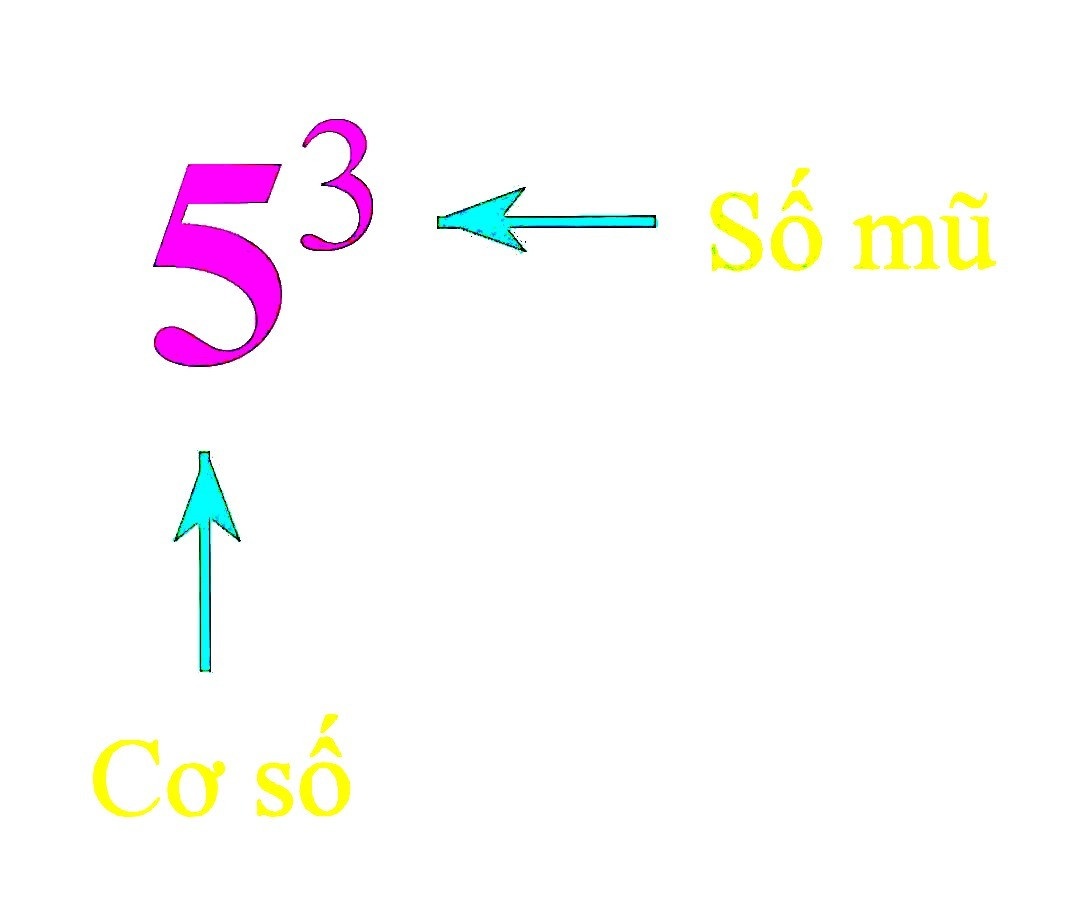
Lý thuyết Lũy thừa với số mũ tự nhiên của một số hữu tỉ chi tiết – Toán lớp 7 Kết nối tri thức (ảnh 1)

+ Tính ${(\frac{- 1}{3})}^{4}$

${(\frac{- 1}{3})}^{4} = \frac{- 1}{3} \cdot \frac{- 1}{3} \cdot \frac{- 1}{3} \cdot \frac{- 1}{3} = \frac{(- 1) \cdot (- 1) \cdot (- 1) \cdot (- 1)}{3 \cdot 3 \cdot 3 \cdot 3} = \frac{1}{81}$

+ Tính và so sánh: $\frac{12^{2}}{6^{2}}$ và ${(- \frac{12}{6})}^{2}$

$\frac{12^{2}}{6^{2}} = \frac{144}{36} = 4$ và ${(- \frac{12}{6})}^{2} = {(- 2)}^{2} = 4$ nên $\frac{12^{2}}{6^{2}} = {(- \frac{12}{6})}^{2}$

Chú ý:

• Lũy thừa của một tích bằng tích các lũy thừa; lũy thừa của một thương bằng thương các lũy thừa.

${(x \cdot y)}^{n} = x^{n} \cdot y^{n}$ ; ${(\frac{x}{y})}^{n} = \frac{x^{n}}{y^{n}}$ (y ≠ 0).

Ví dụ:

${(\frac{3}{4})}^{15} . 4^{15} = {(\frac{3}{4} . 4)}^{15} = 3^{15}$ ;

25³ : 5³= ${(\frac{25}{5})}^{3} = 5^{3} = 125$ .

Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

HĐ 1 trang 16 Toán lớp 7: Viết các tích sau dưới dạng lũy thừa rồi chỉ ra cơ số và số mũ của lũy thừa đó...

HĐ 2 trang 16 Toán lớp 7: Thực hiện phép tính:...

HĐ 3 trang 16 Toán lớp 7: Hãy viết các biểu thức trong HĐ 2 dưới dạng lũy thừa tương tự như lũy thừa của số tự nhiên...

Luyện tập 1 trang 17 Toán lớp 7: Tính:...

Vận dụng trang 17 Toán lớp 7: Viết công thức tính thể tích của hình lập phương cạnh a dưới dạng lũy thừa. Từ đó viết biểu thức lũy thừa đẻ tính toàn bộ lượng nước trên Trái Đất trong bài toán mở đầu (đơn vị kilomét khối)...

HĐ 4 trang 17 Toán lớp 7: Tính và so sánh:...

Luyện tập 3 trang 18 Toán lớp 7: Viết kết quả của các phép tính sau dưới dạng lũy thừa...

HĐ 5 trang 18 Toán lớp 7: Viết số dưới dạng lũy thừa cơ số 2 và số dưới dạng lũy thừa cơ số -3...

Luyện tập 4 trang 18 Toán lớp 7: Viết các số

{(\frac{1}{4})}^{8}; {(\frac{1}{8})}^{3}

dưới dạng lũy thừa cơ số

\frac{1}{2}

Thử thách nhỏ trang 18 Toán lớp 7: Cho hình vuông như Hình 1.12. Em hãy thay mỗi dấu “?” bằng một lũy thừa của 2, biết các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau....

Bài 1.18 trang 18 Toán lớp 7: Viết các số 125; 3 125 dưới dạng lũy thừa của 5...

Bài 1.19 trang 18 Toán lớp 7: Viết các số

{(\frac{1}{9})}^{5}; {(\frac{1}{27})}^{7}

dưới dạng lũy thừa cơ số

\frac{1}{3}

Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung trang 14

Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ

Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế

Luyện tập chung trang 23

Bài tập cuối chương 1

Từ khóa :

toán 7 Giải bài tập Lũy thừa với số mũ tự nhiên của một số hữu tỉ

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

170

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

143

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

118

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.