Với giải Bài 3 trang 79 SBT Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 3: Giải tam giác và ứng dụng thực tế giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải sách bài tập Toán lớp 10 Bài 3: Giải tam giác và ứng dụng thực tế
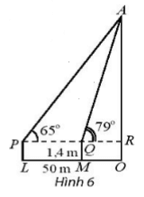
Bài 3 trang 79 SBT Toán 10 Tập 1: Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng = 79°, người đó lùi ra xa một khoảng cách LM = 50m thì nhìn thấy đỉnh tòa nhà với góc nâng = 65°. Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4 m ( Hình 6).
Lời giải
Đặt d = PQ = 50m; h = AR là chiều cao từ giác kế đến đỉnh tòa nhà.
Ta có: = 79° và = 65°
tan = = ⇒ QR = = .
tan = = ⇒ PR = = .
Ta có:
PQ = PR – QR = – = h = 50 (m)
⇒ h ≈ 183,9 (m)
Vậy chiều cao của tòa nhà là AR + RO ≈ 183,9 + 1,4 = 185,3 (m).
Xem thêm các bài giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2 trang 79 SBT Toán 10 Tập 1: Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Định lí côsin và định lí sin
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
