Với giải sách bài tập Toán 10 Bài 2: Tổng và hiệu của hai vectơ sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 2: Tổng và hiệu của hai vectơ
Giải SBT Toán 10 trang 94 Tập 1
Lời giải:
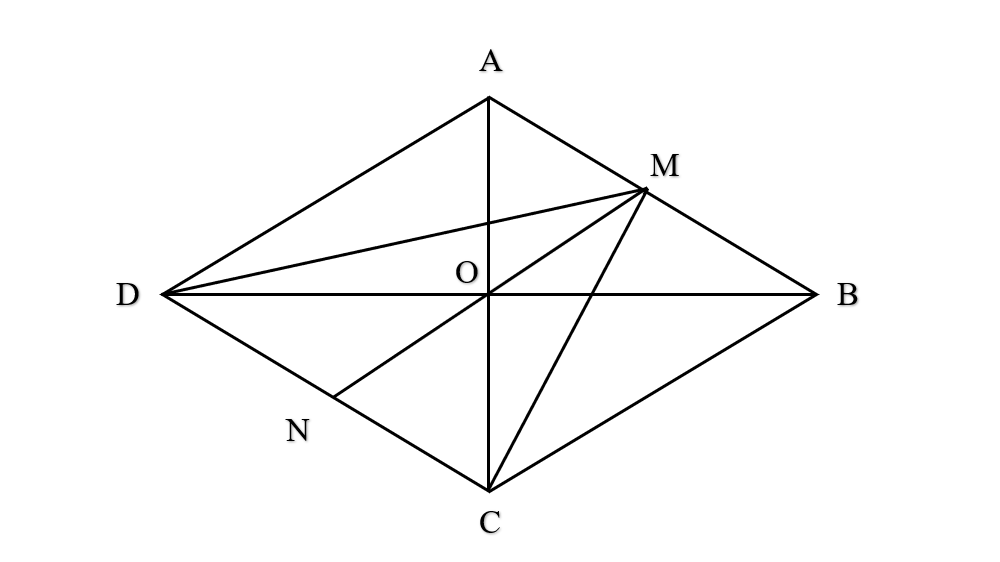
Gọi O là tâm hình thoi. O là trung điểm của AC và BD ( tính chất hình thoi).
⇒ ![]() và
và ![]()
Ta có:
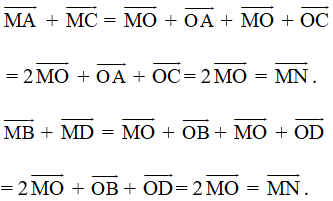
Vậy ![]()
Bài 2 trang 94 SBT Toán 10 Tập 1: Chứng minh rằng với tứ giác ABCD bất kì, ta luôn có:
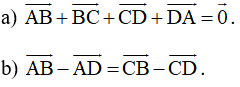
Lời giải:
a) Theo quy tắc ba điểm cộng vectơ ta có:
![]()
Như vậy: ![]()
b) Ta có:
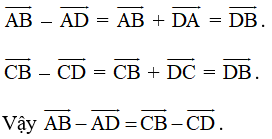
Bài 3 trang 94 SBT Toán 10 Tập 1: Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ và .
Lời giải:
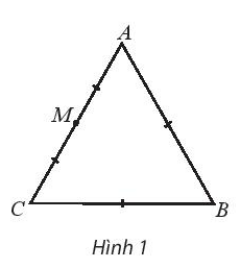
Theo quy tắc ba điểm, ta có: =
Tam giác ABC đều cạnh bằng a nên AC = a.
Do đó = = a.
Gọi M là trung điểm cạnh AC.
Ta có:
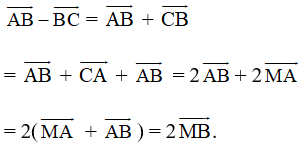
Vì MB là đường trung tuyến của tam giác đều ABC cạnh bằng a nên MB = .
Do đó ![]()
Bài 4 trang 94 SBT Toán 10 Tập 1: Cho hình bình hành ABCD tâm O. Chứng minh rằng:
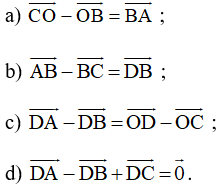
Lời giải:
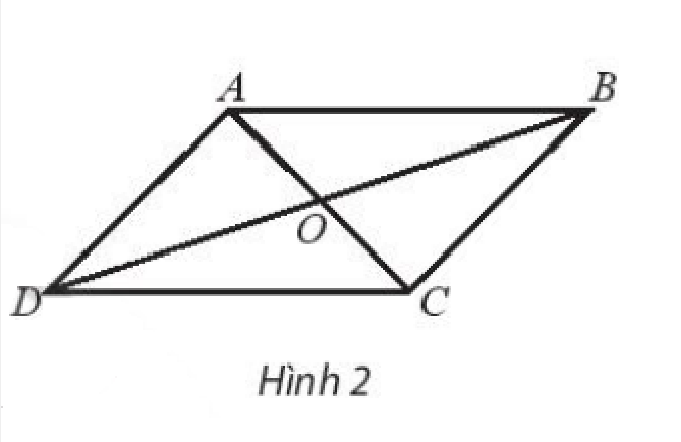
a) Vì ABCD là hình bình hành nên O là trung điểm của AC, BD.
Do đó
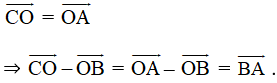
b) Vì ABCD là hình bình hành nên: =
Ta có:
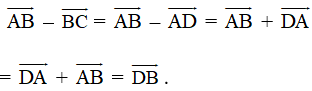
c) Ta có:
![]() và
và ![]()
Mà ta lại có ABCD là hình bình hành nên = .
Vậy nên .
d) Theo chứng minh trên ta có:
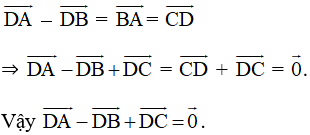
Lời giải:
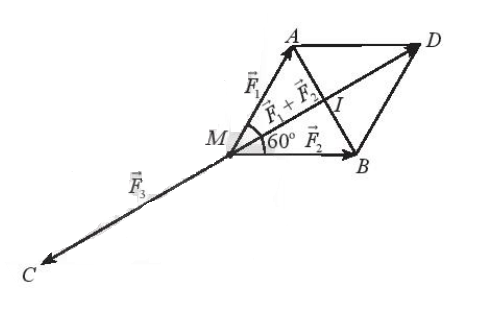
M đứng yên nên:
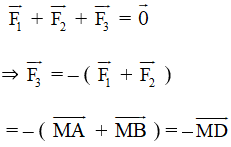
⇒ có hướng ngược với và có độ lớn bằng .
Dựng hình bình hành MADB.
Gọi I là giao điểm của AB và MD. Khi đó I là trung điểm của AB và MD.
Mặt khác = 60° nên tam giác AMB đều.
Khi đó MI ⊥ AB ⇒ Tam giác AIM vuông tại I.
⇒ MI = AM.sin= 100.sin60° = 50 ⇒ MD = 2MI = 100.
Vậy độ lớn của lực bằng 100.
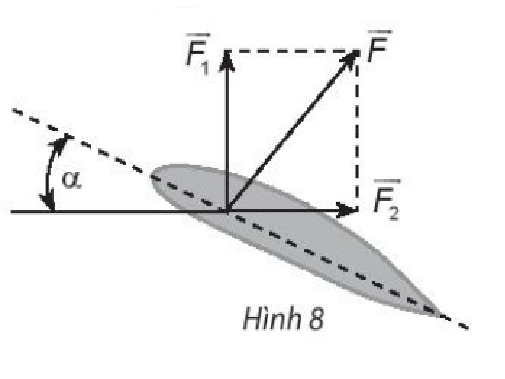
Lời giải:
Đặt tên các điểm trong hình vẽ, ta có:
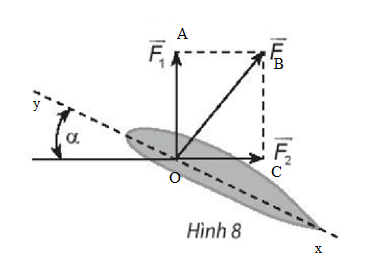
Khi đó
Vì lực ![]() vuông góc với phương xy của cánh nên .
vuông góc với phương xy của cánh nên .
Ta có:
⇒
Xét tam giác BOC vuông tại C, có:
⇔ 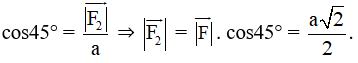
⇔ 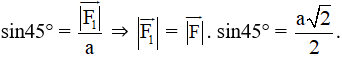
Vậy .
Tìm độ dài các vectơ , .
Lời giải:
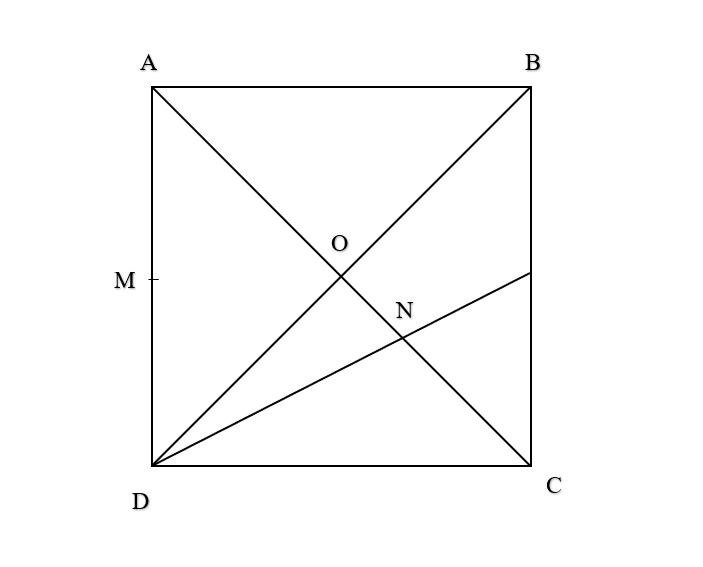
Ta có: suy ra M là trung điểm AD. Khi đó = MA = AD = .
Và suy ra N là trọng tâm tam giác BCD. Khi đó = NO = CO = CA.
Xét hình vuông ABCD, có: CA = =
Suy ra .
Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Tích của một số với một vectơ
Bài 4: Tích vô hướng của hai vectơ
Lý thuyết Tổng và hiệu của hai vectơ
1. Tổng của hai vectơ
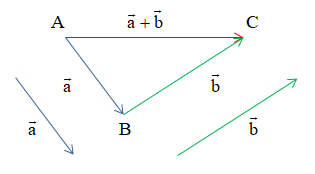
Cho hai vectơ và . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho . Khi đó được gọi là tổng của hai vectơ và và được kí hiệu là .
Vậy .
Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.
Quy tắc ba điểm
Với ba điểm M, N, P, ta có .
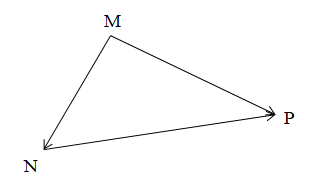 Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.
Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.
Ví dụ: Cho các điểm A, B, C, D, E, F phân biệt. Thực hiện phép cộng các vectơ:
.
Hướng dẫn giải
Áp dụng quy tắc ba điểm, ta có:
.
.
.
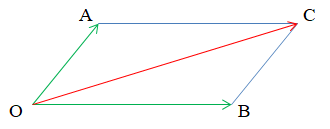
Quy tắc hình bình hành
Nếu OACB là hình bình hành thì ta có .
Ví dụ: Cho hình chữ nhật MNPQ và hai vectơ như hình bên. Tính tổng của hai vectơ và .
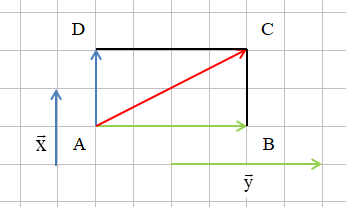
Hướng dẫn giải
Ta có .
Suy ra .
Theo quy tắc hình bình hành, ta có .
Vậy .
2. Tính chất của phép cộng các vectơ
Phép cộng vectơ có các tính chất sau:
+ Tính chất giao hoán: .
+ Tính chất kết hợp: .
+ Với mọi , ta luôn có: .
Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ ,kí hiệu là với .
Ví dụ: Cho tứ giác MNPQ. Thực hiện các phép cộng vectơ sau:
a) .
b) .
Hướng dẫn giải
Áp dụng tính chất giao hoán và tính chất kết hợp của phép cộng vectơ, ta được:
a) .
b) .
Chú ý: Cho vectơ tùy ý .
Ta có .
Tổng hai vectơ đối nhau luôn bằng vectơ-không: .
3. Hiệu của hai vectơ
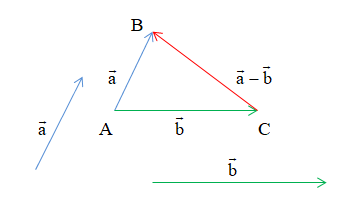
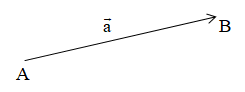
Cho hai vectơ và . Hiệu của hai vectơ và là vectơ \ và kí hiệu là .
Phép toán tìm hiệu của hai vectơ được gọi là phép trừ vectơ.
Ví dụ: Cho các điểm D, E, F, G phân biệt. Thực hiện các phép trừ vectơ sau: .
Hướng dẫn giải
Ta có: .
.
Chú ý: Cho ba điểm O, A, B, ta có:.
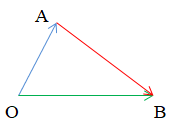 Ví dụ: Cho hình vuông ABCD và một điểm M tùy ý. Thực hiện các phép trừ vectơ sau: .
Ví dụ: Cho hình vuông ABCD và một điểm M tùy ý. Thực hiện các phép trừ vectơ sau: .
Hướng dẫn giải
Ta có .
.
4. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác
Điểm M là trung điểm của đoạn thẳng AB khi và chỉ khi .
Điểm G là trọng tâm của tam giác ABC khi và chỉ khi .
Ví dụ: Cho hình bình hành ABCD có tâm O. Hai điểm E, F lần lượt là trung điểm AB, BC. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
a) .
b) .
Hướng dẫn giải
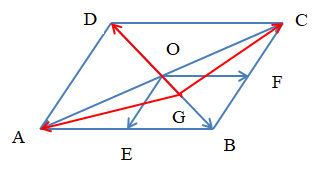 a) Vì ABCD là hình bình hành tâm O nên O là trung điểm AC (tính chất hình bình hành).
a) Vì ABCD là hình bình hành tâm O nên O là trung điểm AC (tính chất hình bình hành).
Lại có E là trung điểm AB (gt)
Do đó OE là đường trung bình của tam giác ABC.
Suy ra OE // BC và OE = = BF (với F là trung điểm BC).
Khi đó ta có tứ giác OEBF là hình bình hành.
Áp dụng quy tắc hình bình hành cho OEBF, ta được: .
Vì ABCD là hình bình hành tâm O nên O là trung điểm AC và BD (tính chất hình bình hành).
Do đó và .
Ta có
.
Vậy .
b) Vì G là trọng tâm của tam giác ABC nên .
Theo quy tắc ba điểm, ta có: .
Ta có
.
Vậy .