Với giải Thực hành 1 trang 69 Toán 8 Tập 1 Chân trời sáng tạo chi tiết trong Bài 3: Hình thang – Hình thang cân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 3: Hình thang – Hình thang cân

Thực hành 1 trang 69 Toán 8 Tập 1: Tìm các góc chưa biết của hình thang MNPQ có hai đáy là MN và QP trong mỗi trường hợp sau và nêu nhận xét của em.

a) $\widehat{Q}=90°$ và $\widehat{N}=125°$.

b) $\widehat{P}=\widehat{Q}=110°$.

Lời giải:

a)

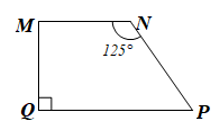
Xét hình thang MNPQ (MN // QP) có $\widehat{Q}=90°$ nên là hình thang vuông.

Suy ra $\widehat{M}=\widehat{Q}=90°$.

Áp dụng định lí tổng các góc của một tứ giác, ta có: $\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360°$

Suy ra $\widehat{P}=360°-\left(\widehat{M}+\widehat{N}+\widehat{Q}\right)$

Do đó $\widehat{P}=360°-\left(90°+90°+125°\right)=55°$.

b)

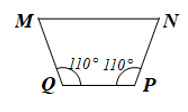
Xét hình thang MNPQ (MN // QP) có $\widehat{P}=\widehat{Q}=110°$ nên là hình thang cân.

Suy ra $\widehat{M}=\widehat{N}=180°-110°=70°$.

Lý thuyết Hình thang – Hình thang cân

Định nghĩa:

– Hình thang là tứ giác có hai cạnh đối song song.

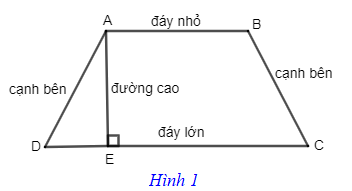
Hình 1là hình thang ABCD với AB // CD. Ta có:

+ Các đoạn thẳng AB, CD gọi là các cạnh đáy (hoặc đáy).

Nếu AB < CD thì AB gọi là đáy nhỏ, CD gọi là đáy lớn.

+ Các đoạn thẳng AD, BC gọi là các cạnh bên.

+ AE là đường vuông góc kẻ từ E đến đường thẳng CD, đoạn thẳng AE gọi là đường cao của hình thang ABCD.

– Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

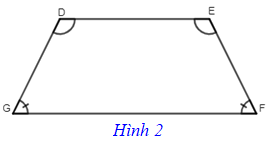
Hình 2 là hình thang cân DEFG với hai đáy là DE và FG có ; .

–Hình thang có một góc vuông được gọi là hình thang vuông.

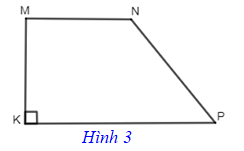
Hình 3 là hình thang vuông MNPK với hai đáy là MN và KP có $\hat{K}=90°$ .

Ví dụ 1. Tìm các góc chưa biết của hình thang ABCD có hai đáy là AB và CD trong các trường hợp sau:

a) $\hat{C}=\hat{D}=60°$;

b) $\hat{A}=90°$và $\hat{B}=50°$.

Hướng dẫn giải

ABCD là hình thang có hai đáy là AB và CD nên AB // CD.

a) Vì $\hat{C}=\hat{D}=60°$nên hình thang ABCD là hình thang cân.

Áp dụng định lí tổng các góc của một tứ giác, ta có: $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$

Do đó: $\hat{A}+\hat{B}=360°-\left(\hat{C}+\hat{D}\right)={360}^{\circ }-(60°+60°)=360°-120°=240°$

Suy ra $\hat{A}=\hat{B}=\frac{240°}{2}=120°$.

b) $\hat{A}=90°$ nên hình thang ABCD là hình thang vuông, suy ra $\hat{A}=\hat{D}=90°$

Áp dụng định lí tổng các góc của một tứ giác, ta có:

$\hat{C}={360}^{\circ }-\left(\hat{A}+\hat{B}+\hat{D}\right)$

Do đó $\hat{C}=360°-\left(90°+50°+90°\right)=360°-230°=130°$