Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 11 Phương trình lượng giác cơ bản, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Phương trình lượng giác cơ bản. Mời các bạn đón xem:

Bài tập Toán 11 Phương trình lượng giác cơ bản

A. Bài tập Phương trình lượng giác cơ bản

Bài 1. Giải các phương trình sau:

Hướng dẫn giải

⇔ x = –60° + k360° (k ∈ ℤ).

Vậy phương trình đã cho có nghiệm là x = –60° + k360° (k ∈ ℤ).

Bài 2. Giải các phương trình sau:

a) sinx.cos2x = sin2x.cos3x;

Hướng dẫn giải

a) sinx.cos2x = sin2x.cos3x.

c) $2{\sin }^2\frac{x}{2}=\cos 5x+1$.

$\iff \cos 5x+1-2{\sin }^2\frac{x}{2}=0$.

⇔ cos5x + cosx = 0.

⇔ 2cos3x.cos2x = 0.

Vậy phương trình đã cho có nghiệm là .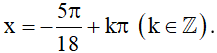

Bài 3.

a) Cho phương trình $\sin \frac{x}{3}=m^2+9$, m là tham số. Với giá trị nào của m thì phương trình đã cho vô nghiệm?

b) Cho phương trình 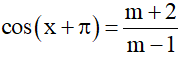, m là tham số. Với giá trị nào của m thì phương trình đã cho có nghiệm?

Hướng dẫn giải

a) TXĐ: D = ℝ.

Phương trình $\sin \frac{x}{3}=m^2+9$ vô nghiệm ⇔ |m² + 9| > 1.

⇔ m² + 9 > 1.

⇔ m² > –8, ∀m ∈ ℝ.

Vậy phương trình $\sin \frac{x}{3}=m^2+9$ vô nghiệm, ∀m ∈ ℝ.

b) TXĐ: D = ℝ.

Phương trình 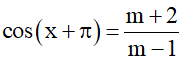 có nghiệm 

Bài 4. Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình 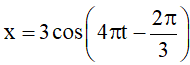, với t là thời gian tính bằng giây và x là quãng đường tính bằng cm. Hãy cho biết trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng bao nhiêu lần?

Hướng dẫn giải

Yêu cầu bài toán ⇔ Tìm t sao cho x = 0, với 0 ≤ t ≤ 5.

Ta có x = 0.

Ta có 0 ≤ t ≤ 5.

$\iff 0\le \frac{7}{24}+\frac{1}{4}k\le 5$.

$\iff -\frac{7}{24}\le \frac{1}{4}k\le \frac{113}{24}$.

$\iff -\frac{7}{6}\le k\le \frac{113}{6}$.

Mà k ∈ ℤ nên k ∈ {–1; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18}.

Có tất cả 20 giá trị k thỏa mãn.

Vậy trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng 20 lần.

Bài 5. Giải các phương trình sau:

a) sin x = $-\frac{\sqrt{3}}{2}$ ;

b) cot (2x – 3) = cot$\frac{\pi }{7}$ .

Hướng dẫn giải

a) sin x = $-\frac{\sqrt{3}}{2}$

⇔ sinx = sin

b) cot (2x – 3) = cot$\frac{\pi }{7}$

⇔ 2x – 3 = $\frac{\pi }{7}$+k$\pi$

⇔ x = $\frac{\pi +21}{14}+k\frac{\pi }{2}$ (k ∈ ℤ).

Bài 6. Giải các phương trình sau:

a) sin x + cos 2x = 0;

b) cos2x = – cos 5x.

Hướng dẫn giải

a) Ta có sin x + cos 2x = 0

⇔ sin x + 1 – 2sin² x = 0

⇔ – 2sin² x + sin x + 1 = 0

⇔ 

+ Với sin x = 1 ta có: sinx = 1 ⇔ $x=\frac{\pi }{2}+k2\pi ,\text{(k}\in \mathbb{Z}\text{).}$

+ Với sin x = $-\frac{1}{2}$ , ta có: sin x = $-\frac{1}{2}$ 

Vậy $x=-\frac{\pi }{6}+k2\pi ,x=\frac{7\pi }{6}+k2\pi ,x=\frac{\pi }{2}+k2\pi ,\text{(k}\in \mathbb{Z}\text{).}$

b) Ta có cos2x = – cos 5x ⇔ cos2x = cos$\left(\pi -5x\right)$

Bài 7. Giải các phương trình lượng giác sau:

a) 2sin²x + 2sinx.cosx – 5cos²x = 0

b) $\sqrt{3}\sin x-\cos x=\sqrt{2}$

Hướng dẫn giải

a) $2si{n}^{2}x+2\sin x.\cos x-5co{s}^2\text{x}=0$

⇔ $2{\tan }^{2}x+3\tan x-5=0$

Vậy phương trình đã cho có nghiệm là $x=\frac{\pi }{4}+k\pi$ hoặc $x\approx 1,2+k\pi$ (k ∈ ℤ).

b) $\sqrt{3}\sin x-\cos x=\sqrt{2}$

⇔ $\frac{\sqrt{3}}{2}\sin x-\frac{1}{2}\cos x=\frac{\sqrt{2}}{2}$

⇔ $\sin x.\cos \frac{\pi }{6}-\cos x.\sin \frac{\pi }{6}=\frac{\sqrt{2}}{2}$

⇔ $\sin \left(x-\frac{\pi }{6}\right)=\sin \frac{\pi }{4}$

Vậy phương trình đã cho có nghiệm là $x=\frac{5\pi }{12}+2k\pi$ hoặc $x=\frac{11\pi }{12}+2k\pi$ (k ∈ ℤ).

Bài 8. Giải phương trình: cos3x.tan5x = sin7x.

Hướng dẫn giải

Điều kiện cos 5x ≠ 0

Khi đó phương trình đã cho trở thành

2sin5x.cos3x = 2sin7x.cos5x

⇔ sin8x = sin12x

• Với $x=\frac{k\pi }{2}$ thì ta có:

$\cos 5x=\cos \frac{5k\pi }{2}=\cos \left(\frac{k\pi }{2}+2k\pi \right)=\cos \left(\frac{k\pi }{2}\right)\ne 0$

⇔ k = 2m (m ∈ ℤ)

• Với $x=\frac{\pi }{20}+\frac{k\pi }{10}$ thì ta có:

$\cos 5x=\cos \left(\frac{\pi }{4}+\frac{k\pi }{2}\right)\ne 0$

 Vậy phương trình đã cho có nghiệm là $x=m\pi ;x=\frac{\pi }{20}+\frac{k\pi }{10}$ (m, k ∈ ℤ).

Bài 9. Tìm x ∈ [0; 14] sao cho: cos3x – 4cos2x + 3cos x – 4 = 0. (1)

Hướng dẫn giải

Ta có: cos3x = 4cos³x – 3cosx

(1) ⇔ cos3x + 3cos x – 4(1 + cos2x) = 0

⇔ 4cos³x – 8cos²x = 0

⇔ 4cos³x.(cos x – 2) = 0

⇔ cos x = 0

⇔ $x=\frac{\pi }{2}+k\pi$ (k ∈ ℤ)

Vì x ∈ [0; 14] ⇒ {$x\in \left\{\frac{\pi }{2};\frac{3\pi }{2};\frac{5\pi }{2};\frac{7\pi }{2}\right\}.$}

Vậy {$x\in \left\{\frac{\pi }{2};\frac{3\pi }{2};\frac{5\pi }{2};\frac{7\pi }{2}\right\}.$}

B. Lý thuyết Phương trình lượng giác cơ bản

1. Phương trình tương đương

- Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.

- Để chỉ sự tương đương của các phương trình, người ta dùng kí hiệu “⇔”.

Ví dụ: Hai phương trình x² – 9 = 0 và 3x² – 27 = 0 có cùng tập nghiệm {–3; 3} nên hai phương trình này tương đương.

2. Phương trình sin x = m

Xét phương trình sin x = m.

• Nếu |m| > 1 thì phương trình vô nghiệm.

• Nếu |m| ≤ 1 thì phương trình có nghiệm:

x = α + k2π, k ∈ ℤ

và x = π – α + k2π, k ∈ ℤ,

với α là góc thuộc [$\left[-\frac{\pi }{2};\frac{\pi }{2}\right]$] sao cho sin α = m.

Chú ý:

Một số trường hợp đặc biệt:

• sin x = 1 ⇔ $x=\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z};$              

• sin x = −1 ⇔ $x=-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z};$

• sin x = 0 ⇔ x = $k\pi ,k\in \mathbb{Z}.$

Ta có:

• sin u = sin v ⇔ u = v + k2π, k ∈ ℤ hoặc u = π – v + k2π, k ∈ ℤ.

• sin x = sin a° ⇔ x = a° + k360°, k ∈ ℤ hoặc x = 180° − a° + k360°, k ∈ ℤ.

Ví dụ: $\sin x=\frac{\sqrt{3}}{2}\iff x=\frac{\pi }{3}+k2\pi$$x=\frac{2\pi }{3}+k2\pi \left(k\in \mathbb{Z}\right).$

3. Phương trình cos x = m

Xét phương trình cos x = m.

• Nếu |m| > 1 thì phương trình vô nghiệm.

• Nếu |m| ≤ 1 thì phương trình có nghiệm:

x = α + k2π, k ∈ ℤ

và x = – α + k2π, k ∈ ℤ,

với α là góc thuộc [0; π] sao cho cos α = m.

Chú ý:

Một số trường hợp đặc biệt:

• cos x = 1 ⇔ x = k2π, k ∈ ℤ;  

• cos x = −1 ⇔ x = π + k2π, k ∈ ℤ;

• cos x = 0 ⇔ $x=\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}.$

Ta có:

• cos u = cos v ⇔ u = v + k2π, k ∈ ℤ hoặc u = –v + k2π, k ∈ ℤ.

• cos x = cos a° ⇔ x = a° + k360°, k ∈ ℤ hoặc x = −a° + k360°, k ∈ ℤ.

Ví dụ: cos x = cos 15° ⇔ x = 15° + k360° hoặc x = −15° + k360°, k ∈ ℤ.

4. Phương trình tan x = m

Với mọi số thực m, phương trình tan x = m có nghiệm

x = α + kπ, k ∈ ℤ,

với α là góc thuộc $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ sao cho tan α = m.

Chú ý: tan x = tan a° ⇔ x = a° + k180°, k ∈ ℤ.

Ví dụ: tan x = 0 ⇔ x = kπ, k ∈ ℤ.

5. Phương trình cot x = m

Với mọi số thực m, phương trình cot x = m có nghiệm

x = α + kπ, k ∈ ℤ,

với α là góc thuộc (0; π) sao cho cot α = m.

Chú ý: cot x = cot a° ⇔ x = a° + k.180°, k ∈ ℤ.

Ví dụ: cot x = 1 ⇔ $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}.$

6. Giải phương trình lượng giác bằng máy tính cầm tay

Ấn liên tiếp các phím SHIFT, sin/cos/tan và giá trị lượng giác của góc lượng giác bất kỳ để tìm ra góc lượng giác đó theo đơn vị radian hoặc theo đơn vị độ.

Chú ý: để giải phương trình cot x = m (m ≠ 0), ta giải phương trình $\tan x=\frac{1}{m}.$

Video bài giảng Toán 11 Bài 4: Phương trình lượng giác cơ bản - Kết nối tri thức