Với giải Luyện tập 4 trang 9 Toán 11 Tập 1 Cánh diều chi tiết trong Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Luyện tập 4 trang 9 Toán 11 Tập 1: Viết công thức biểu thị số đo của các góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác có số đo bằng .
Lời giải:
Gọi α là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác có số đo bằng .
Khi đó, ta có: α = , với k là số nguyên.
Lý thuyết Góc lượng giác
1. Góc hình học và số đo của chúng
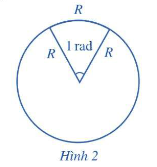
*Nhận xét:
- Đơn vị đo góc: độ hoặc radian (rad).
- Ta có: rad, do đó 1 rad , rad.
- Người ta thường không viết chữ radian hay rad sau số đo góc.
VD: rad cũng được viết là .
2. Góc lượng giác và số đo của chúng
a, Khái niệm
- Cho 2 tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov.
Kí hiệu: (Ou, Ov).
- Mỗi góc lượng giác được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.
b, Tính chất
- Cho hai góc lượng giác = và (O’u’,O’v’) có tia đầu trùng nhau , tia cuối trùng nhau .
Khi đó, nếu sử dụng đợn vị đo là độ thì ta có:
Nếu sử dụng đơn vị đo là radian thì:
* Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
(Ou,Ov) + (Ov, Ow) = (Ou,Ow)
Xem thêm các lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Hoạt động 1 trang 5 Toán 11 Tập 1: Nêu định nghĩa góc trong hình học phẳng...
Hoạt động 2 trang 6 Toán 11 Tập 1: So sánh chiều quay của kim đồng hồ với:...
Luyện tập 7 trang 11 Toán 11 Tập 1: Tìm giá trị lượng giác của góc lượng giác ...
Hoạt động 8 trang 11 Toán 11 Tập 1: Xét dấu các giá trị lượng giác của góc lượng giác α = ‒30°...
Luyện tập 8 trang 11 Toán 11 Tập 1: Xét dấu các giá trị lượng giác của góc lượng giác...
Hoạt động 9 trang 11 Toán 11 Tập 1: Cho góc lượng giác α. So sánh:...
Luyện tập 9 trang 12 Toán 11 Tập 1: Cho góc lượng giác α sao cho và . Tìm cosα...
Hoạt động 10 trang 12 Toán 11 Tập 1: Tìm các giá trị lượng giác của góc lượng giác α = 45°...
Luyện tập 10 trang 12 Toán 11 Tập 1: Tính giá trị của biểu thức:...
Luyện tập 11 trang 14 Toán 11 Tập 1: Tính:...
Luyện tập 12 trang 14 Toán 11 Tập 1: Dùng máy tính cầm tay để tính:...
Bài 2 trang 15 Toán 11 Tập 1: Tính các giá trị lượng giác của mỗi góc sau: 225°; ‒225°; ‒1 035°; ...
Bài 3 trang 15 Toán 11 Tập 1: Tính các giá trị lượng giác (nếu có) của mỗi góc sau:...
Bài 4 trang 15 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α trong mỗi trường hợp sau:...
Bài 5 trang 15 Toán 11 Tập 1: Tính:...
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Bài 2: Các phép biến đổi lượng giác
Bài 3: Hàm số lượng giác và đồ thị