Với giải Bài 86 trang 94 SBT Toán lớp 7 Cánh diều chi tiết trong Bài 12: Tính chất ba đường trung trực của tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài 12: Tính chất ba đường trung trực của tam giác
Bài 86 trang 94 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân ở A. Đường trung trực của cạnh AC cắt AB tại D. Biết CD là tia phân giác của góc ACB. Tính số đo các góc của tam giác ABC.
Lời giải:
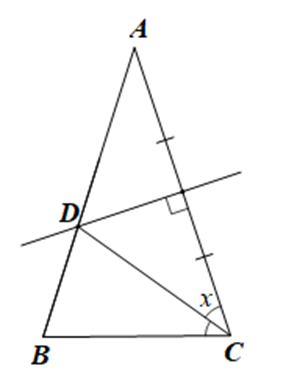
Đặt .
Vì CD là tia phân giác của góc ACB nên .
Vì tam giác ABC cân tại A nên AB = AC, .
Suy ra
Do điểm D nằm trên đường trung trực của canhk AC nên DA = DC.
Do đó tam giác DAC cân ở D nên .
Xét ∆ABC có (tổng ba góc của một tam giác)
Hay 2x + 2x + x = 180° nên 5x = 180°.
Suy ra x = 180°: 5 = 36°.
Do đó .
Vậy số đo các góc A, B, C của tam giác ABC lần lượt là: 36°, 72°, 72°.
Xem thêm các bài giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:
SBT Toán 7 Bài 10 : Tính chất ba đường trung tuyến của tam giác
SBT Toán 7 Bài 11 : Tính chất ba đường phân giác của tam giác
SBT Toán 7 Bài 12 : Tính chất ba đường trung trực của tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
