Với giải sách bài tập Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài 11: Tính chất ba đường phân giác của tam giác
Giải SBT Toán 7 trang 92 Tập 2
a) Điểm E không nằm trên tia phân giác của góc B.
b) .
c) Điểm E cách đều AB, BC, CA.
d) Điểm E nằm trên tia phân giác của góc C.
Lời giải:
Gọi M, N, P lần lượt là hình chiếu của E trên BC, AB, AC.
Khi đó EM ⊥ BC, EN ⊥ AB, EP ⊥ AC và EN = EM.
• Xét ∆BNE và ∆BME có:
,
EN = EM (giả thiết),
BE là cạnh chung
Do đó ∆BNE = ∆BME (cạnh huyền – cạnh góc vuông)
Suy ra (hai góc tương ứng)
Nên điểm E nằm trên tia phân giác của góc ABC.
Do đó phát biểu a là sai.
•Vì AF là tia phân giác của góc BAC nên
Xét DANE và DAPE có:
,
AE là cạnh chung,
(chứng minh trên).
Do đó ∆ANE = ∆APE (cạnh huyền – góc nhọn).
Suy ra EN = EP (hai cạnh tương ứng).
Mà EN = EM (giả thiết)
Nên EM = EN = EP hay điểm E cách đều ba cạnh AB, BC, CA.
Do đó phát biểu c là đúng.
• Xét hai ∆CPE và ∆CME có:
,
EP = EM (chứng mình trên),
CE là cạnh chung
Do đó ∆CPE = ∆CME (cạnh huyền – cạnh góc vuông)
Suy ra (hai góc tương ứng).
Nên điểm E nằm trên tia phân giác của góc ACB.
Do đó phát biểu d là đúng.
• Do AB < AC nên (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn).
Khi đó
Do đó phát biểu b là sai.
Vậy a, b là phát biểu sai; c, d là phát biểu đúng.
a) Số đo góc KAC bằng 30°.
b) Số đo góc BAK bằng 25°.
c) Số đo góc BKC bằng 120°.
d) Số đo góc BKC bằng 115°.
Lời giải:
• Xét ∆ABC có (tổng ba góc của một tam giác)
Mà nên
Suy ra
Xét tam giác ABC có hai tia phân giác của góc B và góc C cắt nhau tại K
Nên AK là tia phân giác của góc BAC.
Suy ra
Do đó phát biểu a là đúng, phát biểu b là sai.
•Vì BK là tia phân giác của góc ABC nên
Vì CK là tia phân giác của góc ACB nên
Suy ra
Mà
Do đó
Xét ∆KBC có (tổng ba góc của một tam giác)
Nên .
Do đó phát biểu c là đúng, phát biểu d là sai.
Vậy phát biểu sai là b và d.
a) I cách đều ba cạnh của tam giác ABC;
b) KI là tia phân giác của góc EKD.
Lời giải:
a) Vì ba đường phân giác của tam giác ABC cùng đi qua một điểm nên giao điểm I của hai đường phân giác BD và CE cũng thuộc đường phân giác xuất phát từ đỉnh A của tam giác ABC.
Suy ra I cách đều ba cạnh AB, BC, AC.
Vậy I cách đều ba cạnh của tam giác ABC.
b) • Vì BD là tia phân giác của góc ABC nên .
Vì CE là tia phân giác của góc ACB nên .
Mà (do tam giác ABC cân tại A).
Suy ra .
• Xét ∆ABD và ∆ACE có:
là góc chung,
AB = AC (do tam giác ABC cân tại A),
(chứng minh trên).
Do đó ∆ABD = ∆ACE (g.c.g).
Suy ra AD = AE (hai cạnh góc vuông).
• Xét ∆ABK và ∆ACK có:
AB = AC (chứng minh trên),
AK là cạnh chung,
BK = CK (do K là trung điểm của BC).
Do đó ∆ABK = ∆ACK (c.c.c).
Suy ra (hai góc tương ứng).
Hay .
• Xét ∆AEK và ∆ADK có:
AE = AD (chứng minh trên),
(chứng minh trên),
AK là cạnh chung.
Do đó ∆AEK = ∆ADK (c.g.c)
Suy ra (hai góc tương ứng)
Nên KA là đường phân giác của góc EKD.
Mặt khác do nên AK là tia phân giác của góc BAC.
Mà theo câu a, I thuộc đường phân giác xuất phát từ đỉnh A của tam giác ABC
Nên AI cũng là đường phân giác của góc BAC.
Do vậy, ba điểm A, I, K thẳng hàng.
Khi đó KI cũng là đường phân giác của góc EKD.
Vậy KI là tia phân giác của góc EKD.
a) EB là tia phân giác của góc DEK, EK là tia phân giác của góc BEA;
b) EC = ED = EK.
Lời giải:
a) Tam giác ABC vuông tại C có (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra .
Tam giác EBK vuông tại K có (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra .
•Vì AE là tia phân giác của góc CAB nên .
Tam giác ACE vuông tại C có (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra
Do đó (hai góc đối đỉnh).
Ta có (cùng bằng 60°) nên EB là tia phân giác của góc DEK.
•Ta có (hai góc kề bù)
Hay
Suy ra .
Do đó (cùng bằng 60°).
Nên EK là tia phân giác của góc BEA.
Vậy EB là tia phân giác của góc DEK, EK là tia phân giác của góc BEA.
b) Xét ∆ACE và ∆AKE có:
,
AE là cạnh chung,
(chứng minh câu a).
Do đó ∆ACE = ∆AKE (cạnh huyền – góc nhọn).
Suy ra CE = KE (hai cạnh tương ứng) (1)
Xét ∆EKB và ∆EDB có:
,
BE là cạnh chung,
(chứng minh câu a)
Do đó ∆EKB = ∆EDB (cạnh huyền – góc nhọn).
Suy ra KE = DE (hai cạnh tương ứng) (2)
Từ (1) và (2) ta có EC = EK = ED.
Vậy EC = ED = EK.
Giải SBT Toán 7 trang 93 Tập 2
Chứng minh:
a) Tam giác EIF là tam giác vuông;
b) IA = IB.
Lời giải:
a) Vì EI là tia phân giác của góc aEF nên .
Vì FI là tia phân giác của góc bFE nên .
Vì a // b nên (hai góc trong cùng phía)
Suy ra .
Xét ∆IEF có (tổng ba góc của một tam giác).
Suy ra
Vậy tam giác EIF là tam giác vuông tại I.
b) Gọi C là hình chiếu của I trên đường thẳng c.
Do EI là tia phân giác của góc AEF nên IA = IC (1)
Do FI là tia phân giác của góc EFB nên IC = IB (2)
Từ (1) và (2) ta có IA = IB.
Vậy IA = IB.
a) Chứng minh: GA, GM, MA lần lượt là tia phân giác của các góc DGE, BGC, EMD.
b) Tìm điều kiện của tam giác ABC để EG là tia phân giác của góc DEM.
Lời giải:
a)• Vì tam giác ABC cân tại A nên AB = AC, .
Vì E là trung điểm của AB nên AE = EB = AB.
Vì D là trung điểm của AC nên AD = CD = AC.
Mà AB = AC nên AE = EB = AD = CD.
Tam giác ABC có hai trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Do đó đường trung tuyến AM của tam giác ABC cũng đi qua G.
Hay ba điểm A, G, M thẳng hàng.
Xét ∆ABM và ∆ACM có:
AB = AC (chứng minh trên),
AM là cạnh chung,
MB = MC (do M là trung điểm của BC).
Do đó ∆ABM = ∆ACM (c.c.c)
Suy ra (hai góc tương ứng)
Xét ∆AEG và ∆ADG có:
AE = AD (chứng minh trên),
(do ),
AG là cạnh chung
Do đó ∆AEG = ∆ADG (c.g.c).
Suy ra (hai góc tương ứng).
Do vậy GA là tia phân giác của góc DGE.
• Ta có (các cặp góc đối đỉnh)
Mà
Nên
Do đó GM là tia phân giác của góc BGC.
• Xét ∆AME và ∆AMD có:
AE = AD (chứng minh trên),
(do ),
AM là cạnh chung,
Do đó ∆AME = ∆AMD (c.g.c).
Suy ra (hai góc tương ứng)
Nên MA là tia phân giác của góc EMD.
Vậy GA, GM, MA lần lượt là tia phân giác của các góc DGE, BGC, EMD.
b) • Xét ∆ABC có (tổng ba góc của một tam giác)
Mà nên (1)
Ta có AE = AD (chứng minh câu a)
Nên tam giác AED cân tại A
Suy ra
Xét ∆ADE có (tổng ba góc của một tam giác)
Mà nên (2)
Từ (1) và (2) suy ra
Mà hai góc này ở vị trí đồng vị
Do đó ED // BC.
Nên (hai góc so le trong)
• Để EG là tia phân giác của góc DEM thì
Suy ra nên tam giác MEC cân tại M.
Do đó ME = MC
Mặt khác, MB = MC nên ME = MB = MC.
Suy ra tam giác EMB cân tại M nên .
• Xét ∆EBC có (tổng ba góc của một tam giác)
Hay
Mà và
Nên hay
Suy ra
Do đó nên
• Xét ∆BEC và ∆AEC có:
(cùng bằng 90°),
EC là cạnh chung,
BE = AE (chứng minh câu a)
Do đó ∆BEC = ∆AEC (hai cạnh góc vuông).
Suy ra BC = AC.
Mà AB = AC (chứng minh câu a).
Do đó AB = BC = AC nên tam giác ABC là tam giác đều.
Vậy điều kiện để EG là tia phân giác của góc DEM là tam giác ABC là tam giác đều.
Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:
SBT Toán 7 Bài 10 : Tính chất ba đường trung tuyến của tam giác
SBT Toán 7 Bài 11 : Tính chất ba đường phân giác của tam giác
SBT Toán 7 Bài 12 : Tính chất ba đường trung trực của tam giác
SBT Toán 7 Bài 13 : Tính chất ba đường cao của tam giác
SBT Toán 7 : Bài tập cuối chương VII
Lý thuyết Tính chất ba đường phân giác của tam giác
1. Đường phân giác của tam giác
– Trong tam giác ABC (hình vẽ bên dưới), tia phân giác của cắt cạnh BC tại D. Khi đó, đoạn thẳng AD được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC.
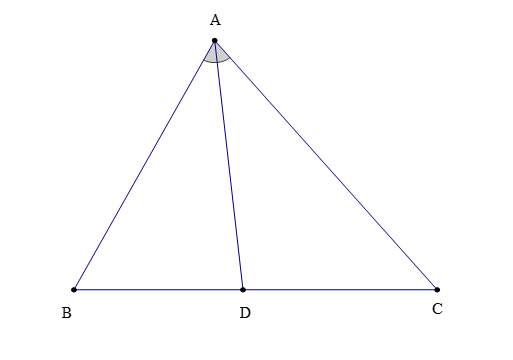
Đôi khi, đường thẳng AD cũng được gọi là đường phân giác của ∆ABC.
Ví dụ: Quan sát hình vẽ và chỉ ra các đường phân giác trong ∆ABC (nếu có):
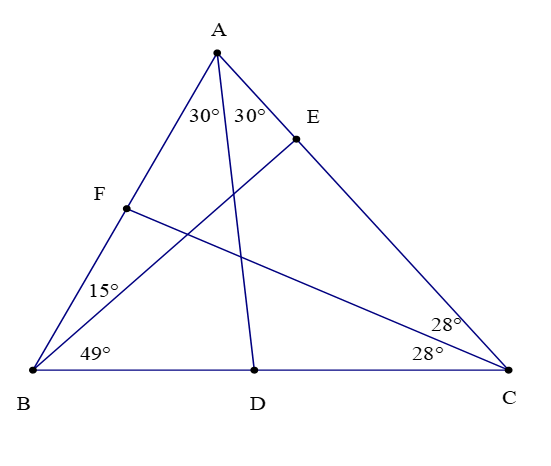
Hướng dẫn giải
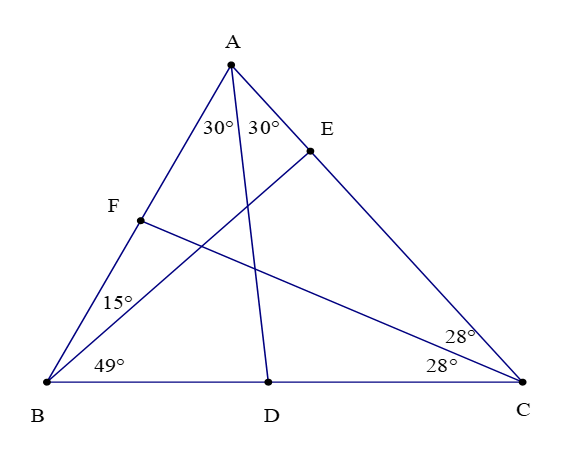
Quan sát hình vẽ trên, ta có:
và D là giao điểm của tia phân giác với cạnh BC. Do đó đoạn thẳng AD là đường phân giác của ∆ABC.
và F là giao điểm của tia phân giác với cạnh AB. Do đó đoạn thẳng CF là đường phân giác của ∆ABC.
Đoạn thẳng BE không là đường phân giác của ∆ABC vì BE không là tia phân giác của của tam giác ABC.
Nhận xét: Mỗi tam giác có ba đường phân giác.
Ví dụ:
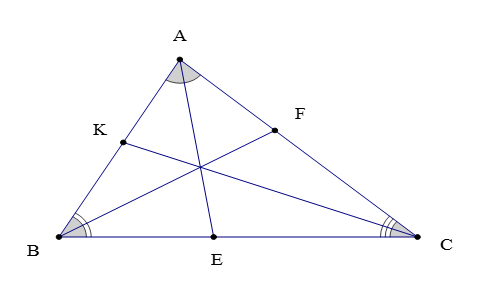
∆ABC có ba đường phân giác AE; BF; CK xuất phát từ ba đỉnh của tam giác này.
2. Tính chất ba đường phân giác của tam giác
– Ba đường phân giác của một tam giác cùng đi qua một điểm
Nhận xét:
+ Để xác định giao điểm ba đường phân giác của một tam giác, ta chỉ cần vẽ hai đường phân giác bất kì và xác định giao điểm của hai đường đó.
+ Giao điểm ba đường phân giác của một tam giác cách đều ba cạnh của tam giác đó.
– Vậy, trong một tam giác ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.
Ví dụ: Cho ∆DEF có I là giao điểm của ba đường phân giác. Kẻ IH ⊥ EF tại H ; IK ⊥ DF tại K. Chứng minh rằng: IF là đường trung trực của đoạn thẳng HK.
Hướng dẫn giải
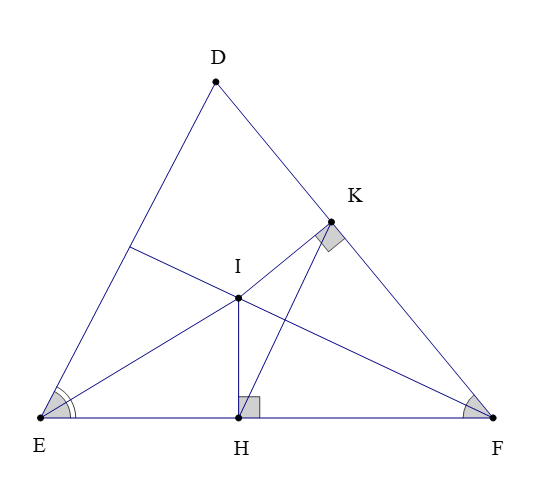
Theo bài ta có: IH ⊥ EF tại H; IK ⊥ DF tại K nên IH; IK lần lượt là khoảng cách từ điểm I tới cạnh EF và DF.
Mà I là giao điểm của ba đường phân giác của ∆DEF (giả thiết)
Do đó IH = IK (tính chất ba đường phân giác của tam giác)
Suy ra I nằm trên đường trung trực của HK (tính chất đường trung trực của đoạn thẳng) (1)
Xét ∆IKF và ∆IHF có:
(IH ⊥ EF tại H ; IK ⊥ DF tại K),
IH = IK (chứng minh trên),
IF là cạnh chung.
Do đó ∆IKF = ∆IHF (cạnh huyền – cạnh góc vuông)
Suy ra FK = FH (hai cạnh tương ứng)
Suy ra F nằm trên đường trung trực của HK (tính chất đường trung trực của đoạn thẳng) (2)
Từ (1) và (2) suy ra I và F nằm trên đường trung trực của HK
Hay IF là đường trung trực của HK
Vậy IF là đường trung trực của đoạn thẳng HK.