Sách bài tập Toán 7 Cánh diều): Bài tập cuối chương VII

Van Anh Ngày: 23-09-2024 Lớp 7

3.6 K

Với giải sách bài tập Toán 7 Bài tập cuối chương VII sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài tập cuối chương VII

Giải SBT Toán 7 trang 98 Tập 2

Bài 99 trang 98 sách bài tập Toán lớp 7 Tập 2: Cho hai tam giác ABC và MNP có $\hat{A B C} = \hat{M N P}$ , $\hat{A C B} = \hat{M P N}$ . Cần thêm một điều kiện để tam giác ABC và tam giác MNP bằng nhau theo trường hợp góc – cạnh – góc là:

A. AC = MP;

B. AB = MN;

C. BC = NP;

D. AC = MN.

Lời giải:

Cho hai tam giác ABC và MNP có góc ABC = góc MNP, góc ACB = góc MPN.Cần thêm một điều kiện để tam giác ABC

Để ΔABC = ∆MNP theo trường hợp góc – cạnh – góc thì hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh bằng nhau của hai tam giác.

Mà $\hat{A B C} = \hat{M N P}, \hat{A C B} = \hat{M P N}$

Lại có $\hat{A B C}$ và $\hat{A C B}$ là hai góc kề cạnh BC;

$\hat{M N P}$ và $\hat{M P N}$ là hai góc kề cạnh NP.

Do đó điều kiện còn thiếu là điều kiện về cạnh, đó là BC = NP.

Vậy ta chọn đáp án C.

Bài 100 trang 98 sách bài tập Toán lớp 7 Tập 2:Cho tam giác ABC có $\hat{B A C} = 110 °$ . Các đường trung trực của AB và AC cắt cạnh BC lần lượt tại E và F. Khi đó, số đo góc EAF bằng:

A. 20°;

B. 30°;

C. 40°;

D. 50°.

Lời giải:

Cho tam giác ABC có góc BAC = 110 độ. Các đường trung trực của AB và AC cắt cạnh BC

Xét tam giác ABC có:

$\hat{B} + \hat{C} + \hat{B A C} = 180 °$ (tổng ba góc trong một tam giác)

Suy ra $\hat{B} + \hat{C} = 180 ° - \hat{B A C} = 180 ° - 110 ° = 70 °$ .

Vì E thuộc đường trung trực của AB nên EB = EA.

Do đó tam giác ABE cân tại E nên $\hat{E A B} = \hat{B}$ .

Vì F thuộc đường trung trực của AC nên FC = FA.

Do đó tam giác ACF cân tại F nên $\hat{F A C} = \hat{C}$ .

Ta có $\hat{B A E} + \hat{E A F} + \hat{F A C} = \hat{B A C}$

Hay $\hat{B} + \hat{E A F} + \hat{C} = \hat{B A C}$

Do đó $\hat{E A F} = \hat{B A C} - (\hat{B} + \hat{C})$

Suy ra $\hat{E A F} = 110 ° - 70 ° = 40 °$ .

Vậy ta chọn đáp án C.

Bài 101 trang 98 sách bài tập Toán lớp 7 Tập 2: Trong các hình 62a, 62b, 62c, 62d, hình nào có điểm cách đều các đỉnh của tam giác đó? Vì sao?

Trong các hình 62a, 62b, 62c, 62d, hình nào có điểm cách đều các đỉnh của tam giác đó

Lời giải:

•Hình 62a:

Xét tam giác ABC có G là giao điểm của ba đường trung tuyến AD, BE, CF nên G là trọng tâm của tam giác ABC.

Do đó G không cách đều ba đỉnh của tam giác ABC

•Hình 62b:

Xét tam giác ABC có I là giao điểm của ba đường phân giác AI, BI, CI nên I cách đều ba cạnh của tam giác ABC.

Do đó I không cách đều ba đỉnh của tam giác ABC

•Hình 62c:

Xét tam giác ABC có O là giao điểm của ba đường trung trực nên OA = OB = OC.

Do đó O cách đều ba đỉnh của tam giác ABC.

•Hình 62d:

Xét tam giác ABC có H là giao điểm của ba đường cao AI, BK, CL nên H là trực tâm của tam giác ABC.

Do đó H không cách đều ba đỉnh của tam giác ABC.

Vậy hình 62c có điểm O cách đều các đỉnh của tam giác ABC.

Bài 102 trang 98 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC và điểm G nằm trong tam giác. Chứng minh: Nếu diện tích các tam giác GAB, GBC và GCA bằng nhau thì G là trọng tâm của tam giác đó.

Lời giải:

Cho tam giác ABC và điểm G nằm trong tam giác. Chứng minh: Nếu diện tích các tam giác GAB, GBC và GCA

Gọi N là giao điểm của AG và BC.

Kẻ BH ⊥ AN (H ∈ AN) và CK ⊥ AN (K ∈ AN).

• Ta có:

$S_{Δ G A B} = \frac{A G . B H}{2}, S_{Δ G C A} = \frac{A G . C K}{2}$

Mà $S_{Δ A G B} = S_{Δ A G C}$ nên $\frac{A G . B H}{2} = \frac{A G . C K}{2}$

Suy ra BH = CK.

•Xét DBHN và DCKN có

$\hat{B H N} = \hat{C K N} (= 90 °)$ ,

BH = CK (chứng minh trên),

$\hat{H N B} = \hat{K N C}$ (hai góc đối đỉnh)

Do đó ∆BHN = ∆CKN (g.c.g)

Suy ra BN = CN (hai cạnh tương ứng)

Hay AN là đường trung tuyến của tam giác ABC.

•Chứng minh tương tự, ta có CG cũng là đường trung tuyến của tam giác ABC.

Tam giác ABC có AN, CG là hai đường trung tuyến cuả tam giác

Mà AN và CG cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Vậy nếu diện tích các tam giác GAB, GBC và GCA bằng nhau thì G là trọng tâm của tam giác đó.

m giác GAB, GBC và GCA bằng nhau thì G là trọng tâm của tam giác đó.

Bài 103 trang 98 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có ba góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC; H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Chứng minh:

a) OC vuông góc với FH;

b) Tam giác OAI là tam giác cân;

c) Tam giác BAI là tam giác cân.

Lời giải:

Cho tam giác ABC có ba góc nhọn, AB < AC < BC. Các tia phân giác của góc A

a) Xét DOHC và DOFC có:

$\hat{O H C} = \hat{O F C} (= 90 °)$ ,

OC là cạnh chung,

$\hat{O C H} = \hat{O C F}$ (do CO là tia phân giác của góc ACB)

Do đó ∆OHC = ∆OFC (cạnh huyền – góc nhọn)

suy ra CH = CF, OH = OF (các cặp cạnh tương ứng).

Do đó C và O cùng nằm trên đường trung trực của đoạn thẳng FH.

Hay CO là đường trung trực của đoạn thẳng FH.

Do đó OC ⊥ FH.

Vậy OC ⊥ FH.

b) Xét ∆OHA và ∆OFI có:

$\hat{O H A} = \hat{O F I} (= 90 °)$ ,

OH = OF (chứng minh câu a),

AH = IF (giả thiết),

Do đó ∆OHA = ∆OFI (hai cạnh góc vuông)

Suy ra OA = OI (hai cạnh tương ứng)

Tam giác OAI có OA = OI nên ∆OAI cân tại O.

Vậy tam giác OAI là tam giác cân tại O.

c) • Kẻ OK ⊥ AB (K ∈ AB).

Xét ∆AOH và ∆AOK có

$\hat{O H A} = \hat{O K A} (= 90 °)$ ,

OA là cạnh chung,

$\hat{H A O} = \hat{K A O}$ (do AO là tia phân giác của góc BAC)

Do đó ∆AOH = ∆AOK (cạnh huyền – góc nhọn)

Suy ra AH = AK (hai cạnh tương ứng).

•Xét tam giác ABC có O là giao điểm của hai tia phân giác của góc ACB và BAC.

Suy ra BO là tia phân giác của góc ABC.

Xét ∆BOK và ∆BOF có

$\hat{O K B} = \hat{O F B} (= 90 °)$ ,

OB là cạnh chung,

$\hat{K B O} = \hat{F B O}$ (do BO là tia phân giác của góc ABC)

Do đó ∆BOK = ∆BOF (cạnh huyền – góc nhọn).

Suy ra BK = BF (hai cạnh tương ứng)

•Ta có AB = AK + KB, BI = BF + FI

Mà BK = BF, AK = IF (=AH)

Từ đó suy ra AB = BI nên tam giác BAI cân tại B.

Vậy tam giác BAI cân tại B.

Giải SBT Toán 7 trang 99 Tập 2

Bài 104 trang 99 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có AB < AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.

a) Chứng minh AC = EB và AC song song với EB.

b) Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. CHứng minh ba điểm I, M, K thẳng hàng.

c) Từ E kẻ EH vuông góc với BC tại H. Cho biết $\hat{H B E} = 50 °; \hat{M E B} = 25 °$ . Tính số đo các góc HEB và HEM.

Lời giải:

Cho tam giác ABC có AB < AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E

a) Xét ∆AMC và ∆EMB có:

AM = ME (giả thiết),

$\hat{A M C} = \hat{E M B}$ (hai góc đối đỉnh),

BM = CM (vì M là trung điểm của BC)

Do đó ∆AMC = ∆EMB (c.g.c)

Suy ra AC = EB (hai cạnh tương ứng) và $\hat{M A C} = \hat{M E B}$ (hai góc tương ứng)

Mà $\hat{M A C}$ và $\hat{M E B}$ ở vị trí so le trong nên AC // BE.

Vậy AC = EB và AC song song với EB.

b) Xét ∆AMI và ∆EMK có:

AM = ME (giả thiết),

$\hat{M A I} = \hat{M E K}$ (do $\hat{M A C} = \hat{M E B}$ ),

AI = EK (giả thiết)

Do đó ∆AMI = ∆EMK (c.g.c)

Suy ra $\hat{A M I} = \hat{E M K}$ (hai góc tương ứng)

Mà $\hat{A M I} + \hat{I M E} = 180 °$ (hai góc kề bù)

Suy ra $\hat{E M K} + \hat{I M E} = 180 °$

Hay $\hat{I M K} = 180 °$

Do đó ba điểm I, M, K thẳng hàng.

Vậy ba điểm I, M, K thẳng hàng.

c) Trong tam giác HBE vuông tại H có:

$\hat{H B E} + \hat{H E B} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $\hat{H E B} = 90 ° - \hat{H B E} = 90 ° - 50 ° = 40 °$ .

Ta có $\hat{H E B} = \hat{H E M} + \hat{M E B}$ (hai góc kề nhau)

Hay $40 ° = \hat{H E M} + 25 °$

Suy ra $\hat{H E M} = 40 ° - 25 ° = 15 °$ .

Vậy $\hat{H E B} = 40 °; \hat{H E M} = 15 °$ .

Bài 105 trang 99 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A có các đường cao BD và CE cắt nhau tại H.

a) Chứng minh ∆ADB = ∆AEC.

b) Chứng minh tam giác HDE là tam giác cân.

c) So sánh HB và HD.

d) Gọi M là trung điểm của HC, N là trung điểm của HB, I là giao điểm của BM và CN. Chứng minh ba điểm A, H, I thẳng hàng.

Lời giải:

Cho tam giác ABC cân tại A có các đường cao BD và CE cắt nhau tại H

a) Xét ∆ABD và ∆ACE có:

$\hat{A D B} = \hat{A E C} (= 90 °)$ ,

AB = AC (do tam giác ABC cân tại A),

$\hat{A}$ là góc chung,

Suy ra ∆ADB = ∆AEC (cạnh huyền – góc nhọn).

Vậy ∆ADB = ∆AEC.

b) Vì ∆ADB = ∆AEC (chứng minh câu a)

Suy ra AD = AE (hai cạnh tương ứng) và $\hat{A B D} = \hat{A C E}$ (hai góc tương ứng).

Ta có AB = AE + EB, AC = AD + DC.

Mà AB = AC, AE = AD.

Suy ra BE = CD.

Xét ∆EHB và ∆DHC có:

$\hat{H E B} = \hat{H D C} (= 90 °)$ ,

BE = CD (chứng minh trên),

$\hat{E B H} = \hat{D C H}$ (do $\hat{A B D} = \hat{A C E}$ )

Suy ra ∆EHB = ∆DHC (cạnh góc vuông – góc nhọn kề).

Do đó HE = HD, BH = CH (các cặp cạnh tương ứng).

Tam giác HDE có HE = HD nên tam giác HDE cân tại H.

Vậy tam giác HDE là tam giác cân tại H.

c) Trong tam giác vuông HDC có HC > HD (trong tam giác vuông, cạnh huyền là cạnh lớn nhất)

Mà HC = HB (chứng minh câu b)

Do đó HB > HD.

Vậy HB > HD.

d) • Gọi P là giao điểm của HI và BC.

Tam giác HBC có BM và CN là hai đường trung tuyến cắt nhau tại I.

Do đó I là trọng tâm của tam giác HBC nên HP là đường trung tuyến xuất phát từ đỉnh H của tam giác.

Từ đó ta có PB = PC.

Xét ∆HBP và ∆HCP có:

HB = HC (chứng minh ở câu b),

HP là cạnh chung,

PB = PC (chứng minh trên)

Do đó ∆HBP = ∆HCP (c.c.c)

Suy ra $\hat{H P B} = \hat{H P C}$ (hai góc tương ứng)

Mà $\hat{H P B} + \hat{H P C} = 180 °$ (hai góc kề bù)

Do đó $\hat{H P B} = \hat{H P C} = \frac{180 °}{2} = 90 °$

Từ đó ta có HP ⊥ BC hay HI ⊥ BC (1)

• Tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm của tam giác ABC.

Do đó AH ⊥ BC (2)

Từ (1) và (2) suy ra ba điểm A, H, I cùng nằm trên một đường thẳng vuông góc với BC tại P

Hay ba điểm A, H, I thẳng hàng.

Vậy ba điểm A, H, I thẳng hàng.

Bài 106 trang 99 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB.

a) Chứng minh $\hat{A B D} = \hat{A E D}$ .

b) Tia ED cắt AB tại F. Chứng minh AC = AF.

c) Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh DI = 2IH.

Lời giải:

Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC

a) Xét DABD và DEAD có:

AB = AE (giả thiết),

$\hat{B A D} = \hat{E A D}$ (do AD là tia phân giác của góc BAC)

AD là cạnh chung

Suy ra ∆ABD = ∆AED (c.g.c)

Do đó $\hat{A B D} = \hat{A E D}$ (hai góc tương ứng)

Vậy $\hat{A B D} = \hat{A E D}$ .

b) Xét ∆ABC và ∆AEF có:

$\hat{F A C}$ là góc chung,

AB = AE (giả thiết),

$\hat{A B C} = \hat{A E F}$ (Do $\hat{A B D} = \hat{A E D}$ )

Suy ra ∆ABC = ∆AEF (g.c.g)

Do đó AC = AF (hai cạnh tương ứng)

Vậy AC = AF.

c) Xét ∆AHF và ∆AHC có:

AH là cạnh chung,

$\hat{F A H} = \hat{C A H}$ (do AD là tia phân giác của góc BAC),

AF = AC (chứng minh câu b)

Do đó ∆AHF = ∆AHC (c.g.c)

Suy ra HF = HC (hai cạnh tương ứng).

Khi đó H là trung điểm của FC nên DH là đường trung tuyến xuất phát từ đỉnh D của tam giác DFC.

Xét tam giác DFC có CG và DH là hai đường trung tuyến, CG và DH cắt nhau tại I

Suy ra I là trọng tâm của tam giác DFC.

Do đó IH = $\frac{1}{2}$ ID (tính chất trọng tâm của tam giác)

Hay DI = 2IH.

Vậy DI = 2IH.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

SBT Toán 7 Bài 10 : Tính chất ba đường trung tuyến của tam giác

SBT Toán 7 Bài 11 : Tính chất ba đường phân giác của tam giác

SBT Toán 7 Bài 12 : Tính chất ba đường trung trực của tam giác

SBT Toán 7 Bài 13 : Tính chất ba đường cao của tam giác

SBT Toán 7 : Bài tập cuối chương VII

Lý thuyết Toán 7 Chương 7: Tam giác

1. Tổng ba góc của một tam giác

– Định lí: Tổng ba góc của một tam giác bằng 180°.

– Chú ý:

+ Tam giác có ba góc cùng nhọn gọi là tam giác nhọn.

+ Tam giác có một góc vuông gọi là tam giác vuông.

+ Tam giác có một góc tù gọi là tam giác tù.

– Nhận xét: Trong một tam giác vuông, tổng hai góc nhọn bằng 90°.

– Góc ngoài của tam giác:

+ Góc ngoài của một tam giác là góc kề bù với một góc trong của một tam giác đó.

+ Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

2. Quan hệ giữa góc và cạnh đối diện trong một tam giác

2.1. Góc đối diện với cạnh lớn hơn

– Trong tam giác ABC:

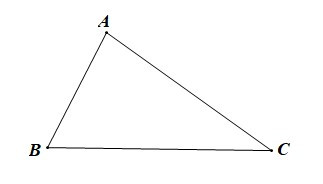
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

• Góc A được gọi là góc đối diện với cạnh BC;

• Góc B được gọi là góc đối diện với cạnh CA;

• Góc C được gọi là góc đối diện với cạnh AB.

– Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Trong tam giác ABC, nếu AC > AB thì $\hat{B} > \hat{C} .$

2.2. Cạnh đối diện với góc lớn hơn

– Trong tam giác ABC:

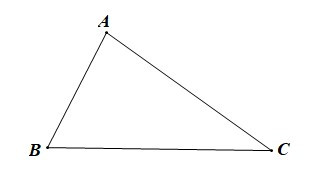
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

• Cạnh BC được gọi là cạnh đối diện với góc A;

• Cạnh CA được gọi là cạnh đối diện với góc B;

• Cạnh AB được gọi là cạnh đối diện với góc C.

– Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Trong tam giác ABC, nếu $\hat{B} > \hat{C}$ thì AC > AB.

– Nhận xét:

+ Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.

+ Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

3. Bất đẳng thức tam giác

– Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Trong tam giác ABC, ta có: AB + BC > AC; AB + AC > BC; AC + BC > AB.

Các bất đảng thức này gọi là các bất đẳng thức tam giác.

– Nhận xét: Trong một tam giác, hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại.

4. Hai tam giác bằng nhau

– Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

– Khi tam giác ABC và tam giác A'B'C' bằng nhau thì ta kí hiệu là: DABC = DA'B'C'.

– Quy ước: Khi viết hai tam giác bằng nhau, tên đỉnh của hai tam giác đó phải viết theo đúng thứ tự tương ứng với sự bằng nhau.

– Chú ý:

+ Nếu AB = A'B', AC = A'C', BC = B'C' và $\hat{A} = \hat{A^{'}}, \hat{B} = \hat{B^{'}}, \hat{C} = \hat{C^{'}}$ thì DABC = DA'B'C'.

+ Nếu DABC = DA'B'C' thì AB = A'B', AC = A'C', BC = B'C' và $\hat{A} = \hat{A^{'}},$ $\hat{B} = \hat{B^{'}},$ $\hat{C} = \hat{C^{'}} .$

Ở đây:

• Hai góc A và A' (B và B', C và C') là hai góc tương ứng;

• Hai cạnh AB và A'B' (BC và B'C', AC và A'C') là hai cạnh tương ứng.

5. Trường hợp bằng nhau cạnh – cạnh – cạnh (c.c.c)

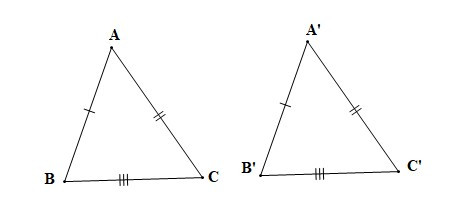
– Tính chất: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Nếu AB = A’B’, AC = A’C’, BC = B’C’ thì DABC = DA’B’C’ (c.c.c).

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Ví dụ: Cho $\hat{xOy},$ trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Vẽ các cung tròn tâm A và B có cùng bán kính sao cho chúng cắt nhau ở điểm I nằm trong góc xOy. Chứng minh OI là tia phân giác của góc xOy.

Hướng dẫn giải

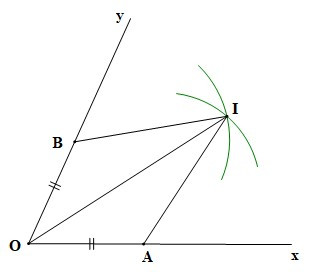
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Vì các cung tròn tâm A và tâm B có cùng bán kính cắt nhau ở điểm I nằm trong góc xOy (giả thiết) nên ta có AI = BI

Xét tam giác OAI và tam giác OBI có:

OA = OB (giả thiết),

AI = BI (chứng minh trên),

OI là cạnh chung.

Suy ra DOAI = DOBI (c.c.c).

Do đó $\hat{AOI} = \hat{BOI}$ (hai góc tương ứng)

Nên tia OI là tia phân giác của góc xOy.

Vậy tia OI là tia phân giác của góc xOy.

– Nhận xét: Cách vẽ tia phân giác của một góc đã được chứng minh cụ thể như trên.

6. Áp dụng vào trường hợp bằng nhau về cạnh huyền và cạnh góc vuông của tam giác vuông

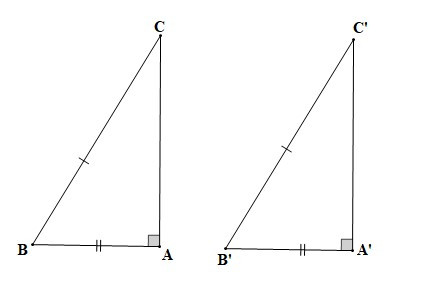
– Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Hai tam giác ABC và A’B’C’ có $\hat{A} = \hat{A^{'}} = 90 °,$ BC = B’C’, AB = A’B’ thì DABC = DA’B’C’ (cạnh huyền – cạnh góc vuông).

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

7. Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)

– Tính chất: Nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Nếu AB = A’B’, $\hat{A} = \hat{A'}$ , AC = A’C’ thì DABC = DA’B’C’ (c.g.c).

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

8. Áp dụng vào trường hợp bằng nhau về hai cạnh góc vuông của tam giác vuông

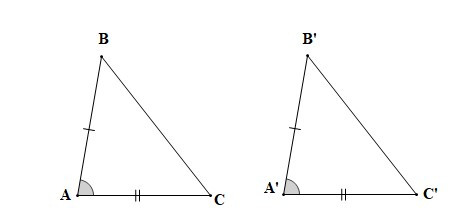
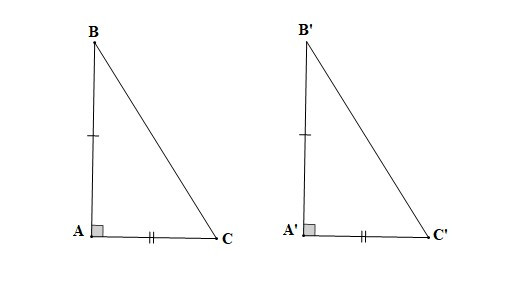
– Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Nếu $\hat{A} = \hat{A'} = 90 °,$ AB = A’B’, AC = A’C’ thì DABC = DA’B’C’.

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

9. Trường hợp bằng nhau góc – cạnh – góc

– Tính chất: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Nếu $\hat{A} = \hat{A^{'}}$ , AB = A’B’, $\hat{B} = \hat{B^{'}}$ thì DABC = DA’B’C’ (g.c.g).

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

10. Áp dụng vào trường hợp bằng nhau về cạnh góc vuông (hoặc cạnh huyền) và góc nhọn của tam giác vuông

10.1. Trường hợp bằng nhau về cạnh góc vuông và góc nhọn của tam giác vuông

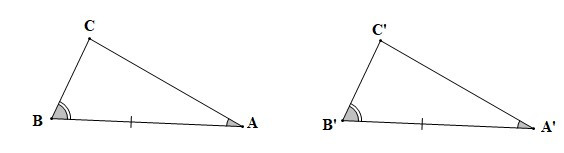
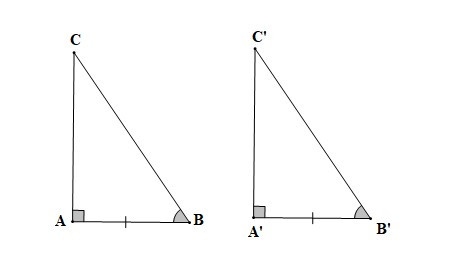
– Nếu một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Nếu $\hat{A} = \hat{A'} = 90 °$ , AB = A’B’, $\hat{B} = \hat{B'}$ thì DABC = DA’B’C’ (cạnh góc vuông – góc nhọn kề).

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

10.2. Trường hợp bằng nhau về cạnh huyền và góc nhọn của tam giác vuông

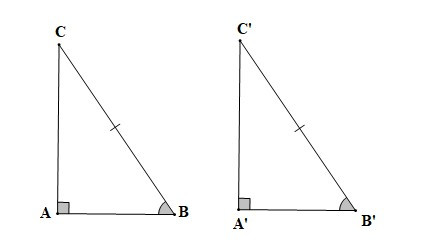
– Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Nếu $\hat{A} = \hat{A'} = 90 °$ , BC = B’C’, $\hat{B} = \hat{B'}$ thì DABC = DA’B’C’ (cạnh huyền – góc nhọn).

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Ví dụ: Cho góc xOy, Oz là tia phân giác của góc đó. Gọi I là một điểm trên tia Oz (I khác O). Kẻ IM vuông góc với Ox (M ∈ Ox), IN vuông góc với Oy (N ∈ Oy). Biết độ dài đoạn thẳng IM là 2 cm, tính độ dài đoạn thẳng IN?

Hướng dẫn giải

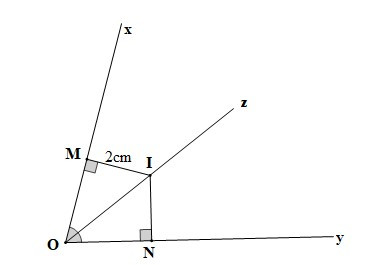
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Xét DOIM và DOIN có:

$\hat{OMI} = \hat{ONI} = 90 °,$

$\hat{IOM} = \hat{ION}$ (do Oz là tia phân giác của $\hat{xOy}$ ),

OI là cạnh chung,

Do đó DOMI = DONI (cạnh huyền – góc nhọn)

Suy ra IM = IN (hai cạnh tương ứng)

Mà IM = 2 cm (giả thiết)

Nên IN = 2 cm.

Vậy độ dài đoạn thẳng IN là 2 cm.

– Nhận xét: Độ dài các đoạn thẳng IM, IN gọi là khoảng cách từ điểm I lần lượt đến hai cạnh Ox, Oy của góc xOy. Như vậy ta có thể nói: Nếu một điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.

Ví dụ: Cho góc xOy nhọn. Gọi A là một điểm nằm trong góc xOy. Kẻ AB vuông góc với Ox (B ∈ Ox), AC vuông góc với Oy (C ∈ Oy). Biết AB = AC. Chứng minh rằng điểm A nằm trên tia phân giác của góc xOy.

Hướng dẫn giải

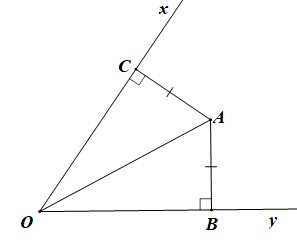
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Xét DOAB và DOAC có:

$\hat{OBA} = \hat{OCA} = 90 °,$

AB = AC (giả thiết),

OA là cạnh chung.

Do đó DABO = DACO (cạnh huyền – cạnh góc vuông)

Suy ra $\hat{BOA} = \hat{AOC}$ (hai góc tương ứng).

Do đó OA là tia phân giác của $\hat{xOy} .$

Nên A là điểm thuộc tia phân giác của góc xOy.

Vậy điểm A nằm trên tia phân giác của góc xOy.

– Nhận xét: Nếu một điểm nằm trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

11. Vẽ tam giác khi biết ba cạnh

Ví dụ: Để vẽ tam giác ABC có AB = 3 cm, AC = 5 cm, BC = 7 cm bằng thước thẳng (có chia đơn vị) và compa, ta làm như sau:

– Bước 1: Vẽ đoạn thẳng AC = 5 cm

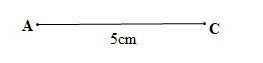
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

– Bước 2: Vẽ một phần đường tròn tâm A bán kính 3 cm và một phần đương tròn tâm C bán kính 7 cm, B là điểm chung của hai phần đường tròn đó

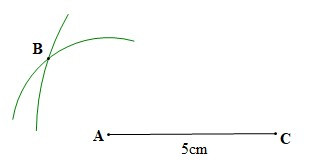
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

– Bước 3: Vẽ các đoạn thẳng AB, BC. Ta được tam giác ABC.

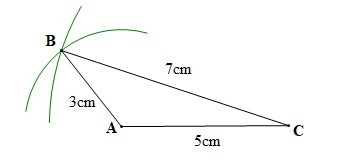
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

12. Vẽ tam giác khi biết hai cạnh và góc xen giữa

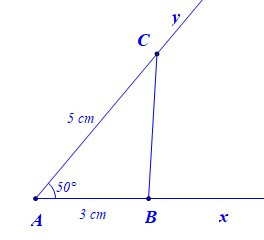
Để vẽ tam giác ABC có AB = 3 cm, AC = 5 cm, $\hat{A} = 50 °$ bằng thước thẳng (có chia đơn vị) và thước đo góc, ta làm như sau:

– Bước 1: Vẽ $\hat{xAy} = 50 °$

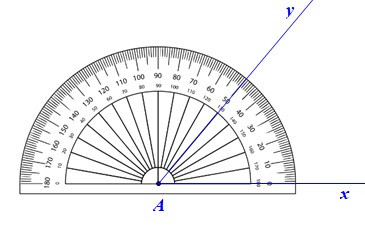
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

– Bước 2: Trên tia Ax lấy điểm B sao cho AB = 3 cm, trên tia Ay lấy điểm C sao cho AC = 5 cm

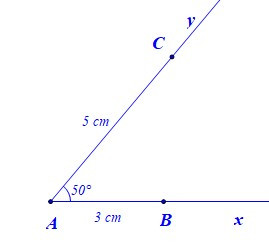
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

– Bước 3: Vẽ đoạn thẳng BC. Ta được tam giác ABC.

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

13. Vẽ tam giác khi biết một cạnh và hai góc kề cạnh đó

Ví dụ: Để vẽ tam giác ABC có AB = 5 cm, $\hat{A} = 60 °, \hat{B} = 70 °$ bằng thước thẳng (có chia đơn vị) và thước đo góc, ta làm như sau:

– Bước 1: Vẽ đoạn thẳng AB = 5 cm

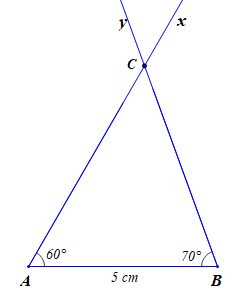
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

– Bước 2: Vẽ các tia Ax, By sao cho $\hat{BAx} = 60 °, \hat{ABy} = 70 °$

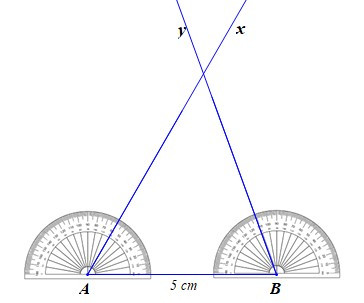
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

– Bước 3: Vẽ C là điểm chung của hai tia Ax và By. Ta nhận được tam giác ABC.

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

14. Tam giác cân

14.1. Định nghĩa

Tam giác cân là tam giác có hai cạnh bằng nhau.

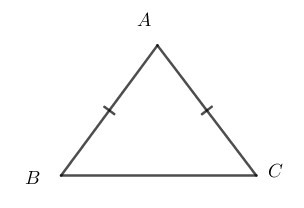
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Cho tam giác cân ABC có AB = AC. Khi đó, ta gọi:

• Tam giác ABC là tam giác cân tại A;

• AB, AC là các cạnh bên và BC là cạnh đáy;

• $\hat{B}, \hat{C}$ là các góc ở đáy và $\hat{A}$ là góc ở đỉnh.

14.2. Tính chất

Trong một tam giác cân, hai góc ở đáy bằng nhau.

Chú ý:

+ Tam giác vuông có hai cạnh góc vuông bằng nhau được gọi là tam giác vuông cân.

+ Trong tam giác vuông cân, mỗi góc ở đáy bằng 45°.

14.3. Dấu hiệu nhận biết

– Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

– Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Chú ý:

+ Tam giác có ba cạnh bằng nhau là tam giác đều.

+ Tam giác cân có một góc bằng 60° là tam giác đều.

14.4. Vẽ tam giác cân

Ví dụ: Dùng thước thẳng (có chia đơn vị) và compa vẽ tam giác HEG cân tại H có cạnh bên HE = HG = a

Để vẽ tam giác HEG, ta làm theo các bước:

– Bước 1: Vẽ đoạn thẳng EG.

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

– Bước 2: Vẽ cung tròn tâm E bán kính a và cung tròn tâm G bán kính a. Hai cung tròn cắt nhau tại H.

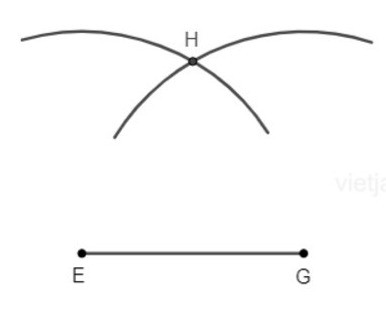
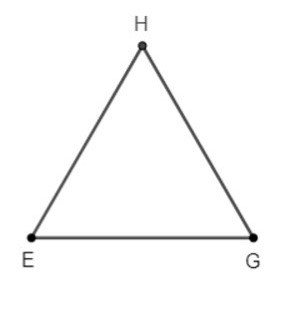
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

– Bước 3: Vẽ các đoạn HE, HG. Ta nhận được tam giác HEG cân tại H.

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

15. Đường vuông góc và đường xiên

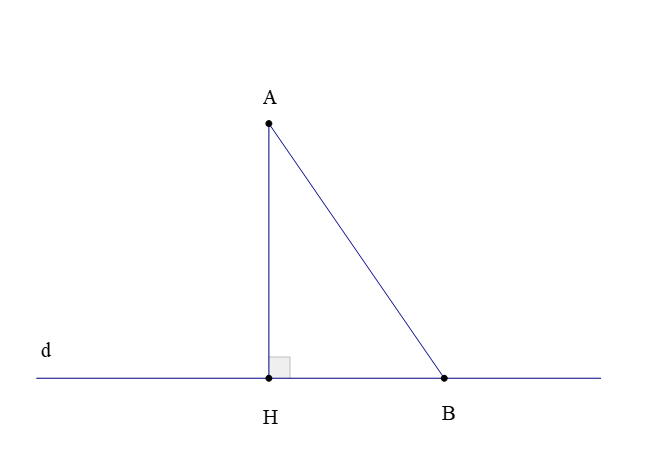
Trong hình vẽ trên, ta gọi:

– Đoạn thẳng AH là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d;

– Điểm H là chân của đường vuông góc hay hình chiếu của điểm A trên đường thẳng d;

– Độ dài đoạn thẳng AH là khoảng cách từ điểm A đến đường thẳng d;

– Đoạn thẳng AB là một đường xiên kẻ từ điểm A đến đường thẳng d.

16. Quan hệ giữa đường vuông góc và đường xiên

– Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.

17. Đường trung trực của một đoạn thẳng

17.1. Định nghĩa

– Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng ấy.

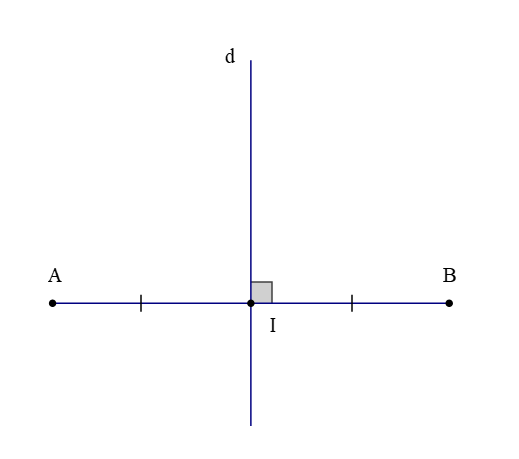
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Quan sát hình vẽ trên, ta có:

+ Đoạn thẳng AB; trung điểm I của đoạn thẳng AB;

+ Đường thẳng d ⊥ AB tại I.

Do đó, đường thẳng d là đường trung trực của đoạn thẳng AB.

17.2. Tính chất

– Một điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

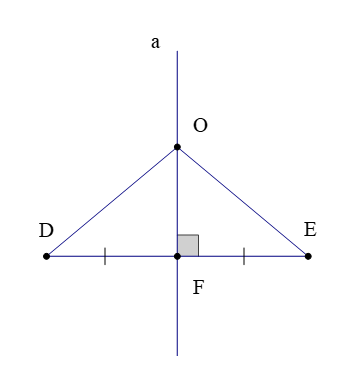
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Quan sát hình trên, ta có:

Đường thẳng a là đường trung trực của đoạn thẳng DE;

Điểm O nằm trên đường thẳng a.

Khi đó ta có OD = OE.

– Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Gọi d là đường trung trực của đoạn thẳng AB, M là điểm sao cho MA = MB (như hình vẽ bên dưới). Ta có M nằm trên đường trung trực d của đoạn thẳng AB.

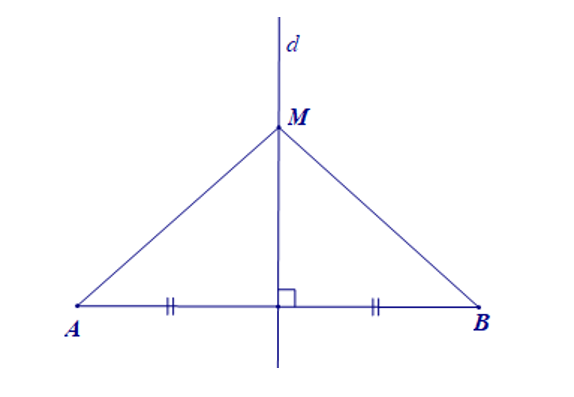
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

17.3. Vẽ đường trung trực của một đoạn thẳng

Ví dụ: Dùng thước thẳng (có chia đơn vị) và compa vẽ đường trung trực của đoạn thẳng AB, biết AB = a cm.

Để vẽ đường trung trực của đoạn thẳng AB, ta làm theo các bước:

Bước 1: Vẽ đoạn thẳng AB = a cm.

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Bước 2: Vẽ một phần đường tròn tâm A bán kính R (biết R > $\frac{a}{2}$ ).

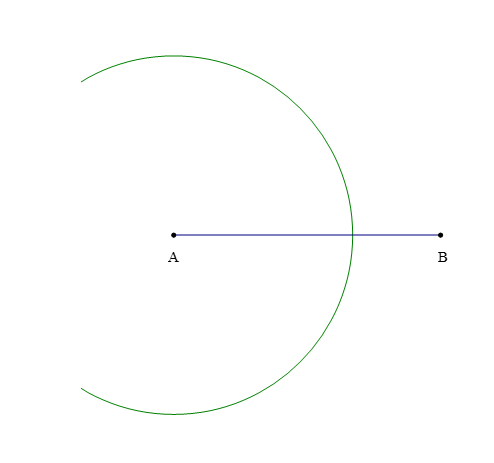
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Bước 3: Vẽ một phần đường tròn tâm B bán kính R (biết R > $\frac{a}{2}$ ), cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm C và D.

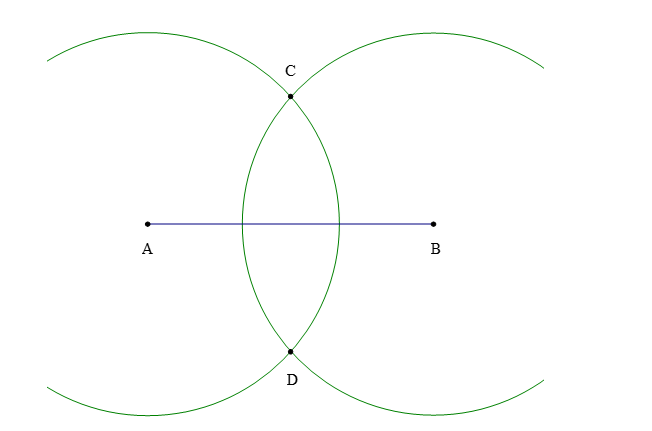
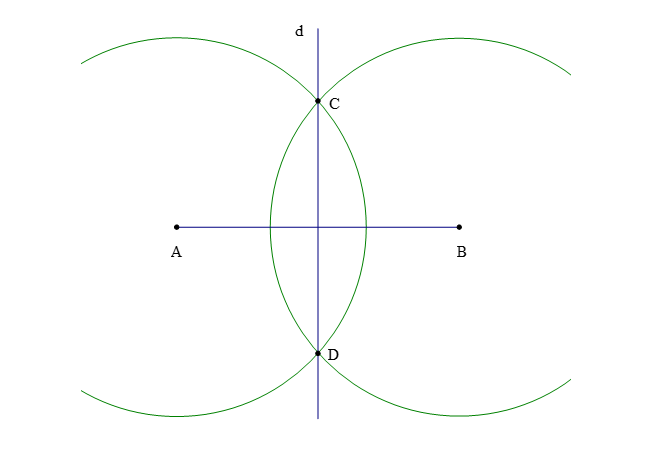
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Bước 4: Vẽ đường thẳng đi qua hai điểm C và D. Đường thẳng CD là đường trung trực của đoạn thẳng AB.

Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

18. Tính chất ba đường trung tuyến của tam giác

18.1. Đường trung tuyến của tam giác

– Trong tam giác ABC (hình bên dưới), đoạn thẳng AM nối đỉnh A với trung điểm M của cạnh BC được gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc tương ứng với cạnh BC).

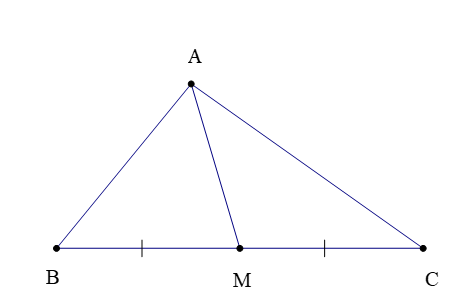
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Đôi khi, đường thẳng AM cũng được gọi là đường trung tuyến của ∆ABC.

– Chú ý: Mỗi tam giác có ba đường trung tuyến.

18.2. Tính chất ba đường trung tuyến của tam giác

– Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó được gọi là trọng tâm của tam giác.

Chú ý: Trong tam giác ABC (hình vẽ dưới) có ba đường trung tuyến AM, BK, CN cùng đi qua điểm G, ta còn nói chúng đồng quy tại điểm G.

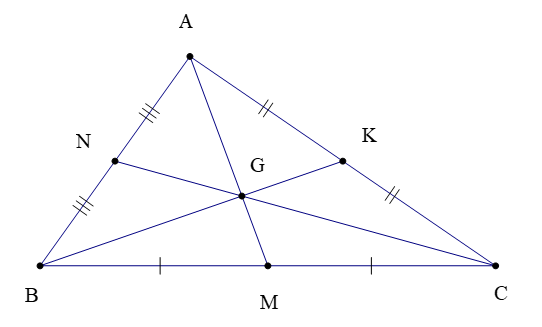
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Để xác định trọng tâm của một tam giác, ta chỉ cần vẽ hai đường trung tuyến bất kì và xác định giao điểm của hai đường đó.

Nhận xét: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

Lưu ý: Trong ∆ABC, với AM là đường trung tuyến và G là trọng tâm ta có:

$\frac{GM}{AM} = \frac{1}{3}, \frac{GM}{GA} = \frac{1}{2}$

19. Tính chất ba đường phân giác của tam giác

19.1. Đường phân giác của tam giác

– Trong tam giác ABC (hình vẽ bên dưới), tia phân giác của $\hat{A}$ cắt cạnh BC tại D. Khi đó, đoạn thẳng AD được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC.

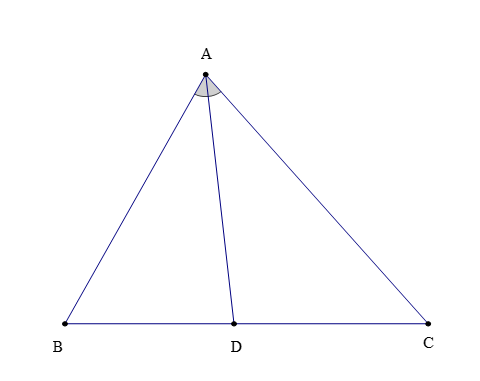
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Đôi khi, đường thẳng AD cũng được gọi là đường phân giác của ∆ABC.

Nhận xét: Mỗi tam giác có ba đường phân giác.

19.2. Tính chất ba đường phân giác của tam giác

– Ba đường phân giác của một tam giác cùng đi qua một điểm

Nhận xét:

+ Để xác định giao điểm ba đường phân giác của một tam giác, ta chỉ cần vẽ hai đường phân giác bất kì và xác định giao điểm của hai đường đó.

+ Giao điểm ba đường phân giác của một tam giác cách đều ba cạnh của tam giác đó.

– Vậy, trong một tam giác ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.

20. Tính chất ba đường trung trực của tam giác

20.1. Đường trung trực của tam giác

– Trong một tam giác, đường trung trực của mỗi cạnh được gọi là đường trung trực của tam giác đó.

Chú ý: Đường trung trực của một tam giác có thể không đi qua đỉnh nào của tam giác.

– Nhận xét: Mỗi tam giác có 3 đường trung trực.

20.2. Tính chất ba đường trung trực của tam giác

– Ba đường trung trực của một tam giác cùng đi qua một điểm.

Nhận xét:

+ Để xác định giao điểm ba đường trung trực của một tam giác, ta chỉ cần vẽ hai đường trung trực bất kì và xác định giao điểm của hai đường đó.

+ Giao điểm ba đường trung trực của một tam giác cách đều ba đỉnh của tam giác đó.

Do đó, trong một tam giác ba đường trung trực cùng đi qua một điểm và điểm đó cách đều ba đỉnh của tam giác.

21. Tính chất ba đường cao của tam giác

21.1. Đường cao của tam giác

– Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là một đường cao của tam giác đó.

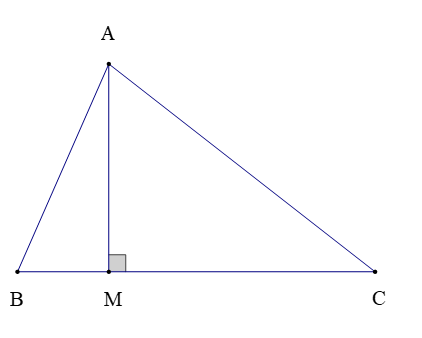
Ôn tập chương 7 (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Trong hình vẽ trên, đoạn thẳng AM là một đường cao của tam giác ABC. Đôi khi, ta cũng gọi đường thẳng AM là một đường cao của tam giác ABC.

Chú ý:

+ Mỗi tam giác có ba đường cao.

+ Đường cao của tam giác có thể nằm trong, trên cạnh hoặc nằm ngoài tam giác.

21.2. Tính chất ba đường cao trong tam giác

– Trong một tam giác, ba đường cao cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác.

Nhận xét: Để xác định trực tâm của một tam giác, ta chỉ cần vẽ hai đường cao bất kì và xác định giao điểm của hai đường đó.

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

169

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

143

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

116

Tìm kiếm