Với giải Bài 44 trang 83 SBT Toán lớp 7 Cánh diều chi tiết trong Bài 7: Tam giác cân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 7: Tam giác cân

Bài 44 trang 83 sách bài tập Toán lớp 7 Tập 2: Ở Hình 36 có AB song song cới CD, BC song song với AD. Tia phân giác của góc BAD cắt BC tại E và cắt tia DC tại F.

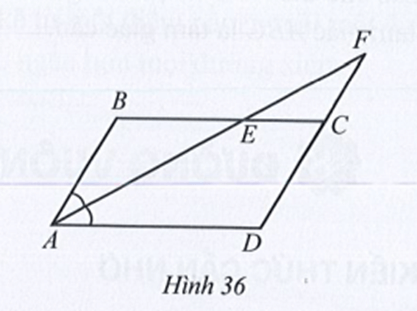
a) Chứng minh các tam giác ABE, CEF, DAF là các tam giác cân.

b) Tính số đo mỗi góc của tam giác ADF, biết $\widehat{BAD}=60°$.

Lời giải:

a) • Vì AE là tia phân giác của $\widehat{BAD}$ nên $\widehat{BAE}=\widehat{EAD}$.

Vì BC // AD nên $\widehat{BEA}=\widehat{EAD}$ (hai góc so le trong)

Do đó $\widehat{BAE}=\widehat{BEA}$.

Suy ra tam giác ABE cân tại B.

• Vì AB // CD nên $\widehat{BAE}=\hat{F}$ (hai góc so le trong).

Mà $\widehat{BAE}=\widehat{BEA}$(chứng minh trên), $\widehat{CEF}=\widehat{BEA}$ (hai góc đối đỉnh).

Suy ra $\widehat{CEF}=\hat{F}$.

Nên tam giác CEF cân tại C.

• Ta có $\widehat{BAF}=\widehat{\text{DAF}}$ và $\widehat{BAF}=\widehat{DFA}$ nên $\widehat{DAF}=\widehat{DFA}$.

Do đó tam giác DAF cân tại D.

Vậy ∆ABE cân tại B, ∆CEF cân tại C, ∆DAF cân tại D.

b) Vì AB // CD nên $\widehat{BAD}+\widehat{ADF}=180°$ (hai góc trong cùng phía)

Suy ra $\widehat{ADF}=180°-\widehat{BAD}=180°-60°=120°$

Xét ∆ADF có $\widehat{ADF}+\widehat{DFA}+\widehat{DAF}=180°$ (tổng ba góc của một tam giác).

Mà $\widehat{ADF}=120°$, $\widehat{DAF}=\widehat{DFA}$.

Nên $\widehat{DAF}=\widehat{DFA}=\frac{180°-\widehat{ADF}}{2}=\frac{180°-120°}{2}=30°$.

Vậy $\widehat{DAF}=\widehat{DFA}=30°,\widehat{FDA}=120°.$