Với giải sách bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 8: Đường vuông góc và đường xiên

Giải SBT Toán 7 trang 85 Tập 2

Bài 52 trang 85 sách bài tập Toán lớp 7 Tập 2: Cho góc xOy và điểm B thuộc tia Ox, B ≠ O. Vẽ H là hình chiếu của điểm B trên đường thẳng Oy trong các trường hợp sau:

a) $\widehat{xOy}$ là góc nhọn;

b) $\widehat{xOy}$ là góc vuông;

c) $\widehat{xOy}$ là góc tù.

Lời giải:

a) $\widehat{xOy}$ là góc nhọn

b) $\widehat{xOy}$ là góc vuông

c) $\widehat{xOy}$ là góc tù

Bài 53 trang 85 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A có H là hình chiếu của A trên đường thẳng BC, lấy điểm M nằm giữa A và H. Chứng minh:

a) BH = CH;

b) MB = MC;

c) MA < AC.

Lời giải:

a) Vì tam giác ABC cân tại A nên AB = AC.

Xét ∆AHB và ∆AHC có:

$\widehat{AHB}=\widehat{AHC}\left(=90°\right)$,

BA = AC (chứng minh trên),

AH là cạnh chung

Do đó ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông).

Suy ra BH = CH (hai cạnh tương ứng).

Vậy BH = CH.

b) Vì ∆ABH = ∆ACH (chứng minh câu a)

Suy ra $\widehat{HAB}=\widehat{HAC}$ (hai góc tương ứng).

Xét ∆AMB và ∆AMC có:

BA = AC (chứng minh câu a),

$\widehat{MAB}=\widehat{MAC}$ (do $\widehat{HAB}=\widehat{HAC}$),

AM là cạnh chung

Do đó ∆ABM = ∆ACM (c.g.c).

Suy ra BM = CM (hai cạnh tương ứng).

Vậy BM = CM.

c) Vì $\widehat{AMC}$ là góc ngoài của tam giác CMH tại đỉnh M

Nên $\widehat{AMC}=\widehat{MHC}+\widehat{MCH}$

Mà $\widehat{MHC}=90°$ nên $\widehat{AMC}$ là góc tù

Xét tam giác AMC có $\widehat{AMC}$ là góc tù

Nên MC < AC (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất).

Vậy MC < AC.

Bài 54 trang 85 sách bài tập Toán lớp 7 Tập 2: Từ một điểm A nằm ngoài đường thẳng d, vẽ đường vuông góc AH và các đường xiên AB, AC tùy ý (Hình 40).

a) So sánh độ dài AH và AB, AH và AC.

b) Chứng minh: Nếu AB = AC thì HB = HC; ngược lại, nếu HB = HC thì AB = AC.

Lời giải:

a) Ta có AH và AB lần lượt là đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng d.

Suy ra AH < AB.

Tương tự, AH và AC lần lượt là đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng d.

Suy ra AH < AC.

Vậy AH < AB và AH < AC.

b) • Nếu AB = AC.

Xét ∆AHB và ∆AHC có:

$\widehat{AHB}=\widehat{AHC}\left(=90°\right)$,

AB = AC (giả thiết),

AH là cạnh chung

Do đó ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông).

Suy ra BH = CH (hai cạnh tương ứng).

• Nếu BH = CH

Xét ∆AHB và ∆AHC có:

$\widehat{AHB}=\widehat{AHC}\left(=90°\right)$,

BH = CH (giả thiết),

AH là cạnh chung

Do đó ∆ABH = ∆ACH (hai cạnh góc vuông).

Suy ra AB = AC (hai cạnh tương ứng).

Vậy nếu AB = AC thì HB = HC; ngược lại, nếu HB = HC thì AB = AC.

Bài 55 trang 85 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A, M là trung điểm của AC.

a) Vẽ E là hình chiếu của A trên đường thẳng BM.

b) Vẽ F là hình chiếu của C trên đường thẳng BM.

c) Chứng minh BE + BF > 2AB.

Lời giải:

a)

b)

c) Xét ∆MAE và ∆MCF có:

$\widehat{AEM}=\widehat{CFM}\left(=90°\right)$,

MA = MC (vì M là trung điểm của AC),

$\widehat{AME}=\widehat{CMF}$ (hai góc đối đỉnh)

Do đó ∆MAE = ∆MCF (cạnh huyền – góc nhọn).

Suy ra ME = MF (hai cạnh tương ứng).

Ta có BA và BM lần lượt là đường vuông góc và đường xiên kẻ từ điểm B xuống đường thẳng AC

Suy ra AB < BM.

Hay AB < BE + EM (1) và AB < BF – MF (2)

Cộng vế theo vế của (1) và (2) ta có:

AB + AB < BE + EM + BF – MF

Mà ME = MF

Do đó 2AB < BE + BF.

Vậy BE + BF > 2AB.

Bài 56 trang 85 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC vuông cân tại A. Một đường thẳng a đi qua A. Gọi M và N lần lượt là hình chiếu của B và C trên đường thẳng a. Chứng minh:

a) $\widehat{ABM}=\widehat{CAN}$;

b) CN = MA;

c) Nếu a song song với BC thì MA = AN.

Lời giải:

a) Xét ∆MAB vuông tại M có: $\widehat{ABM}+\widehat{MAB}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90^o).

Ta có $\widehat{MAB}+\widehat{BAC}+\widehat{CAN}=180°$

Suy ra $\widehat{MAB}+\widehat{CAN}=180°-\widehat{BAC}=90°$

Lại có $\widehat{ABM}+\widehat{MAB}=90°$

Suy ra $\widehat{ABM}=\widehat{CAN}$.

Vậy $\widehat{ABM}=\widehat{CAN}$.

b) Xét ∆MAB và ∆NCA có:

$\widehat{BMA}=\widehat{ANC}\left(=90°\right)$,

BA = AC (vì tam giác ABC vuông cân tại A),

$\widehat{ABM}=\widehat{CAN}$ (chứng minh câu a).

Do đó ∆MAB = ∆NCA (cạnh huyền – góc nhọn).

Suy ra MA = NC (hai cạnh tương ứng).

Vậy MA = NC.

c) Vì tam giác ABC cân tại A nên $\widehat{ACB}=\widehat{ABC}$

Lại có $\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180°$ (tổng ba góc của tam giác ABC)

Suy ra $\widehat{ACB}=\widehat{ABC}=\frac{180°-90°}{2}=45°$.

• Nếu a // BC thì $\widehat{MAB}=\widehat{ABC}$ (hai góc so le trong).

Do đó $\widehat{MAB}=45°$.

Xét ∆ABM có $\widehat{AMB}+\widehat{MBA}+\widehat{MAB}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{MBA}=180°-\widehat{AMB}-\widehat{MAB}=180°-90°-45°=45°$.

Do đó $\widehat{MAB}=\widehat{MBA}$ (cùng bằng 45°).

Xét ∆AMB có $\widehat{AMB}=90°$ và $\widehat{MAB}=\widehat{MBA}$ nên ∆AMB vuông cân tại M.

Suy ra MA = MB (1)

• Nếu a // BC thì $\widehat{CAN}=\widehat{ACB}=45°$ (hai góc so le trong)

Xét ∆ABM có $\widehat{ACN}+\widehat{ANC}+\widehat{CAN}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{ACN}=180°-\widehat{ANC}-\widehat{CAN}=180°-90°-45°=45°$.

Do đó $\widehat{ACN}=\widehat{CAN}$ (cùng bằng 45°).

Xét ∆ANC có $\widehat{ANC}=90°$ và $\widehat{ACN}=\widehat{CAN}$ nên ∆ANC vuông cân tại N.

Suy ra CN = AN (2)

Từ (1) và (2) suy ra MA = AN.

Vậy MA = AN.

Giải SBT Toán 7 trang 86 Tập 2

Bài 57 trang 86 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh độ dài AD và DC.

Lời giải:

Kẻ DH ⊥ BC.

Vì BD là tia phân giác của góc ABC nên ${\hat{B}}_1={\hat{B}}_2$.

Xét ∆DAB và ∆DHB có:

$\widehat{BAD}=\widehat{BHD}\left(=90°\right)$,

BD là cạnh chung,

${\hat{B}}_1={\hat{B}}_2$ (chứng minh trên)

Do đó ∆DAB = ∆DHB (cạnh huyền – góc nhọn).

Suy ra AD = HD (hai cạnh tương ứng) (1)

Vì ∆DHC vuông tại H nên HD < DC (trong tam giác vuông, cạnh huyển là cạnh lớn nhất) (2)

Từ (1) và (2) suy ra AD < DC.

Vậy AD < DC.

Bài 58 trang 86 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A (AB < AC), BD là tia phân giác của góc ABC (D ∈ AC). Qua C kẻ tia Cx vuông góc với AC cắt BD tại M.

a) Chứng minh tam giác CBM là tam giác cân.

b) So sánh độ dài CM và AC.

Lời giải:

a) Vì ∆ABD vuông tại A nên ${\hat{B}}_1+{\hat{D}}_1=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90^o)

Mà ${\hat{B}}_1={\hat{B}}_2$ (do BD là tia phân giác của góc ABC) và ${\hat{D}}_1={\hat{D}}_2$ (hai góc đối đỉnh).

Nên ${\hat{B}}_2+{\hat{D}}_2=90°$

Vì ∆CDM vuông tại C nên $\hat{M}+{\hat{D}}_2=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90^o).

Suy ra $\hat{M}={\hat{B}}_2$

Do đó tam giác CBM cân tại C.

Vậy tam giác CBM cân tại C.

b) Vì tam giác CBM cân tại C (chứng minh câu a)

Nên CM = BC.

Vì ∆ABC vuông tại A nên BC > AC (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).

Suy ra CM > AC.

Vậy CM > AC.

Bài 59 trang 86 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có $\hat{B}$ và $\hat{C}$ nhọn. H và K lần lượt là hình chiếu của B và C trên Ax (Hình 41).

Chứng minh:

a) BH + CK ≤ BC.

b) Nếu tổng BH + CK lớn nhất thì tia Ax phải vuông góc với BC.

Lời giải:

a) Vì ∆BHE vuông tại H nên BH ≤ BE (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).

Vì ∆CKE vuông tại K nên CK ≤ CE (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).

Suy ra BH + CK ≤ BE + CE = BC.

Vậy BH + CK ≤ BC.

b) Ta có BH + CK ≤ BC (theo câu a).

Do đó BH + CK lớn nhất khi BH + CK = BC

Điều này xảy ra khi và chỉ khi BH = BE, CK = CE.

Khi đó BH ≡ BE, CK ≡ CE

Do đó BE ⊥ Ax và CE ⊥ Ax

Hay BC ⊥ Ax.

Vậy nếu tổng BH + CK lớn nhất thì tia Ax phải vuông góc với BC.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

SBT Toán 7 Bài 7 : Tam giác cân

SBT Toán 7 Bài 8 : Đường vuông góc và đường xiên

SBT Toán 7 Bài 9 : Đường trung trực của một đoạn thẳng

SBT Toán 7 Bài 10 : Tính chất ba đường trung tuyến của tam giác

SBT Toán 7 Bài 11 : Tính chất ba đường phân giác của tam giác

Lý thuyết Đường vuông góc và đường xiên

1. Đường vuông góc và đường xiên

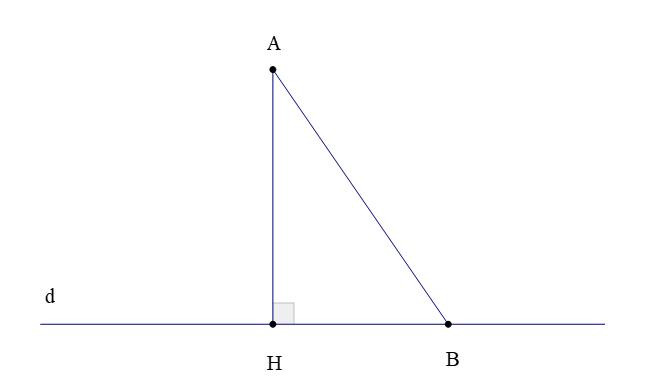
Trong hình vẽ trên, ta gọi:

– Đoạn thẳng AH là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d;

– Điểm H là chân của đường vuông góc hay hình chiếu của điểm A trên đường thẳng d;

– Độ dài đoạn thẳng AH là khoảng cách từ điểm A đến đường thẳng d;

– Đoạn thẳng AB là một đường xiên kẻ từ điểm A đến đường thẳng d.

Ví dụ: Quan sát hình vẽ dưới đây:

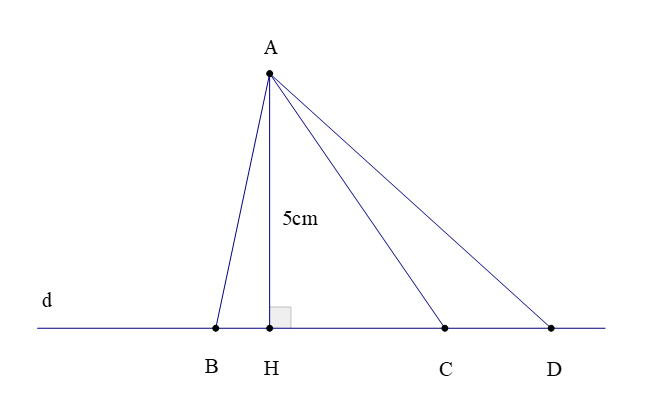
Hãy cho biết:

a) Hình chiếu của điểm A trên đường thẳng d; khoảng cách từ điểm A đến đường thẳng BD bằng độ dài đoạn thẳng nào?

b) Đoạn thẳng nào là đường xiên kẻ từ điểm A đến đường thẳng d?

Hướng dẫn giải

a) Vì AH vuông góc với đường thẳng d tại H do đó:

Hình chiếu của điểm A trên đường thẳng d là điểm H.

Khoảng cách từ điểm A đến đường thẳng BD là AH = 5cm (do BD ≡ d).

b) Các đoạn thẳng AB; AC; AD là các đường xiên kẻ từ A đến đường thẳng d.

2. Quan hệ giữa đường vuông góc và đường xiên

– Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.

Ví dụ: Qua điểm O nằm ngoài đường thẳng a kẻ đường thẳng vuông góc với đường thẳng a và cắt a tại B. Lấy hai điểm A và C nằm trên đường thẳng a và nằm về hai phía so với điểm B sao cho $\widehat{\text{OAB}}=60°$; $\widehat{\text{OCB}}=45°.$ So sánh độ dài các đoạn thẳng OA; OB; OC.

Hướng dẫn giải

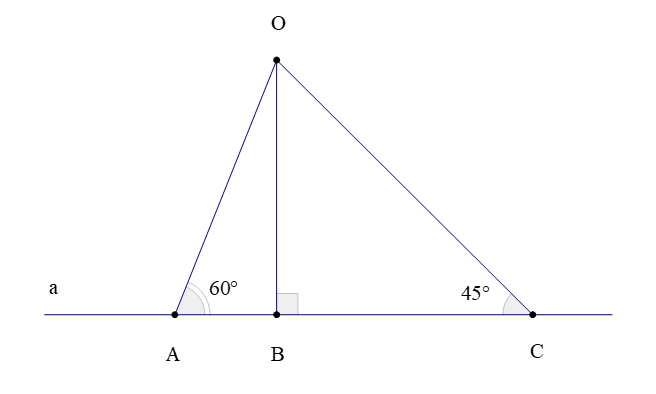
Vì OB là đường vuông góc kẻ từ điểm O đến đường thẳng a và OA; OC là các đường xiên kẻ từ O đến đường thẳng a nên OB là đoạn thẳng ngắn nhất

Do đó OB < OA; OB < OC (1)

Xét ∆OAC có $\widehat{\text{OAC}}>\widehat{\text{OCA}}$ (vì 60° > 45°)

Suy ra: OC > OA (quan hệ giữa góc và cạnh đối diện trong tam giác) (2)

Từ (1) và (2) suy ra: OB < OA < OC.

Vậy OB < OA < OC.