Với giải sách bài tập Toán 7 Bài 9: Đường trung trực của một đoạn thẳng sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 9: Đường trung trực của một đoạn thẳng

Giải SBT Toán 7 trang 87 Tập 2

Bài 60 trang 87 sách bài tập Toán lớp 7 Tập 2: Xác định điểm M thuộc đường thẳng BC sao cho M cách đều A và B trong mỗi trường hợp sau:

a) Tam giác nhọn ABC;

b) Tam giác ABC có góc B là góc tù;

c) Tam giác ABC vuông tại B.

Lời giải:

Vì M cách đều A và B nên M nằm trên đường trung trực d của đoạn thẳng AB.

Như vậy M nằm trên đường thẳng BC và M nằm trên đường trung trực d của AB.

a) Tam giác ABC nhọn thì điểm M thuộc tia BC (hình vẽ):

b) Tam giác ABC có góc B là góc tù thì M thuộc tia đối của tia BC (hình vẽ):

c) Tam giác ABC vuông tại B thì d // BC nên không tìm được M (hình vẽ):

Bài 61 trang 87 sách bài tập Toán lớp 7 Tập 2: Một con đường liên xã cách không xa hai địa điểm dân cư và hai địa điểm này nằm ở cùng một phía của con đường. Hãy xác định một địa điểm trên con đường đó để xây dựng nhà văn hóa xã sao cho nhà văn hóa đó cách đều hai địa điểm dân cư.

Lời giải:

Đưa về bài toán: Cho đường thẳng d và hai điểm A, B nằm cùng một phía đối với d. Tìm một điểm C trên d sao cho C cách đều A và B.

+) Trường hợp 1: Khi AB không vuông góc với d, vẽ trung trực a của đoạn thẳng AB. Giao điểm của đường thẳng a và đường thẳng d chính là điểm C cần tìm.

Vì C nằm trên đường trung trực a của đoạn thẳng AB nên theo tính chất đường trung trực ta có C cách đều A và B (CA = CB).

+) Trường hợp 2: Khi AB ⊥ d thì a // d, do đó không có một điểm nào nằm trên d lại cách đều A và B.

Vậy địa điểm để xây dựng nhà văn hóa là điểm nằm trên con đường và trung trực của đoạn đường giữa hai điểm dân cư.

Bài 62 trang 87 sách bài tập Toán lớp 7 Tập 2: Quan sát Hình 44, biết ∆MAB = ∆NAB. Chứng minh đường thẳng AB là đường trung trực của đoạn thẳng MN.

Lời giải:

Vì ∆MAB = ∆NAB (giả thiết)

Suy ra AM = AN, BM = BN (các cặp cạnh tương ứng).

Do đó A và B cùng cách đều hai điểm M, N.

Suy ra A và B cùng nằm trên đường trung trực của đoạn thẳng MN.

Hay đường thẳng AB là đường trung trực của đoạn thẳng MN.

Vậy đường thẳng AB là đường trung trực của đoạn thẳng MN.

Bài 63 trang 87 sách bài tập Toán 7 Tập 2:Cho tam giác ABC có AB < AC. Đường trung trực của đoạn thẳng BC cắt cạnh AC tại M. Chứng minh AM + BM = AC.

Lời giải:

Vì M thuộc đường trung trực của BC (giả thiết)

Nên BM = CM (tính chất đường trung trực của một đoạn thẳng)

Ta có: AM + BM = AM + CM = AC.

Vậy AM + BM = AC.

Bài 64 trang 87 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A có $\hat{C}=30°$. Đường trung trực của BC cắt AC tại M. Chứng minh:

a) BM là tia phân giác của góc ABC;

b) MA < MC.

Lời giải:

a) Vì DABC vuông tại A nên $\widehat{ABC}+\hat{C}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90^o).

Suy ra $\widehat{ABC}=90°-\hat{C}=90°-30°=60°$.

Vì điểm M thuộc đường trung trực của BC nên MB = MC.

Do đó tam giác MBC cân ở M.

Suy ra ${\hat{B}}_1=\hat{C}=30°$

Mặt khác ${\hat{B}}_1+{\hat{B}}_2=\widehat{ABC}=60°$ (hai góc kề nhau)

Nên ${\hat{B}}_2=\widehat{ABC}-{\hat{B}}_1=60°-30°=30°$

Suy ra ${\hat{B}}_2={\hat{B}}_1$

Do đó BM là tia phân giác của góc ABC.

Vậy BM là tia phân giác của góc ABC.

b) Trong tam giác vuông ABM có MA < MB (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).

Mà MB = MC (chứng minh câu a).

Suy ra MA < MC.

Vậy MA < MC.

Bài 65 trang 87 sách bài tập Toán lớp 7 Tập 2: Quan sát Hình 45, biết AM là đường trung trực của đoạn thẳng BC và DB = DC. Chứng minh ba điểm A, M, D thẳng hàng.

Lời giải:

Vì DB = DC (giả thiết) nên điểm D thuộc đường trung trực của đoạn thẳng BC.

Mà AM là đường trung trực của đoạn thẳng BC (giả thiết).

Do đó ba điểm A, M, D cùng nằm trên đường trung trực của đoạn thẳng BC.

Hay ba điểm A, M, D thẳng hàng.

Vậy ba điểm A, M, D thẳng hàng.

Giải SBT Toán 7 trang 88 Tập 2

Bài 66 trang 88 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A có M là trung điểm BC; ME vuông góc với AB tại E, MF vuông góc với AC tại F. Chứng minh:

a) AM là trung trực của đoạn thẳng BC;

b) ME = MF và AM là đường trung trực của đoạn thẳng EF.

Lời giải:

a) Tam giác ABC cân tại A nên AB = AC (hai cạnh bên).

Suy ra A thuộc đường trung trực của BC.

Lại có M là trung điểm của BC.

Nên AM là đường trung trực của BC.

Vậy AM là trung trực của đoạn thẳng BC.

b) Vì tam giác ABC cân tại A nên $\hat{B}=\hat{C}$ (hai góc ở đáy).

Xét ∆EBM và ∆FCM có:

$\widehat{BEM}=\widehat{CFM}\left(=90°\right)$,

BM = CM (do M là trung điểm của BC),

$\hat{B}=\hat{C}$ (chứng minh trên)

Do đó ∆EBM = ∆FCM (cạnh huyền – góc nhọn).

Suy ra ME = MF, BE = CF (các cặp cạnh tương ứng).

Do đó M thuộc đường trung trực của EF (1)

Ta có AB = AE + EB, AC = AF + FC.

Mà AB = AC, BE = CF nên AE = AF.

Suy ra A thuộc đường trung trực của EF (2)

Từ (1) và (2) suy ra AM là đường trung trực của EF.

Vậy ME = MF và AM là đường trung trực của EF.

Bài 67 trang 88 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A. Đường trung trực của đoạn thẳng AC cắt cạnh AB tại D. Biết CD là tia phân giác của góc ACB. Tính số đo mỗi góc của tam giác ABC.

Lời giải:

Đường trung trực của AC cắt AB tại D nên DA = DC.

Do đó tam giác ADC cân tại D.

Suy ra $\hat{A}={\hat{C}}_1$

Vì CD là tia phân giác của góc C nên ${\hat{C}}_1={\hat{C}}_2=\frac{1}{2}\widehat{ACB}$

Suy ra $\hat{A}={\hat{C}}_1={\hat{C}}_2=\frac{1}{2}\widehat{ACB}$

Hay $\widehat{ACB}=2\hat{A}$

Vì tam giác cân ABC nên $\hat{B}=\widehat{ACB}$ (hai góc ở đáy).

Do đó $\hat{B}=\widehat{ACB}=2\hat{A}.$

Mà $\hat{A}+\hat{B}+\widehat{ACB}=180°$ (tổng ba góc của tam giác ABC).

Suy ra $\hat{A}+2\hat{A}+2\hat{A}=180°$ hay $5\hat{A}=180°$

Nên $\hat{A}=36°$

Khi đó $\hat{B}=\widehat{ACB}=2.36°=72°$

Vậy ∆ABC có $\hat{B}=\hat{C}=72°,\hat{A}=36°.$

Bài 68 trang 88 sách bài tập Toán lớp 7 Tập 2: Cho góc xOy khác góc bẹt. Oz là tia phân giác của góc đó, M là một điểm bất kì thuộc tia Oz. Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C. Qua M vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh:

a) OM là đường trung trực của đoạn thẳng AB;

b) Tam giác DMC là tam giác cân.

Lời giải:

a) Vì Oz là tia phân giác của góc xOy nên $\widehat{xOz}=\widehat{zOy}$.

Xét ∆OAM và ∆OBM có

$\widehat{OAM}=\widehat{OBM}\left(=90°\right)$,

OM là cạnh chung,

$\widehat{AOM}=\widehat{BOM}$ (do $\widehat{xOz}=\widehat{zOy}$)

Do đó ∆OAM = ∆OBM (cạnh huyền – góc nhọn).

Suy ra OA = OB và MA = MB (các cặp cạnh tương ứng).

Nên O và M cùng nằm trên đường trung trực của AB.

Vậy OM là đường trung trực của AB.

b) Xét ∆ADM và ∆BCM có

$\widehat{DAM}=\widehat{CBM}\left(=90°\right)$,

AM = BM (chứng minh câu a),

$\widehat{AMD}=\widehat{BMC}$ (hai góc đối đỉnh)

Do đó ∆ADM = ∆BCM (cạnh huyền – góc nhọn).

Suy ra MD = MC (hai cạnh tương ứng).

Do đó tam giác CDM cân tại M.

Vậy tam giác DMC cân tại M.

Bài 69 trang 88 sách bài tập Toán lớp 7 Tập 2: Cho góc xOy nhọn. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Đường trung trực của đoạn thẳng OA và đường trung trực của đoạn thẳng OB cắt nhau tại I. Chứng minh:

a) OI là tia phân giác của góc xOy;

b) OI là đường trung trực của đoạn thẳng AB.

Lời giải:

Gọi D và F lần lượt là trung điểm của OA và OB.

a) Ta có:

DI là đường trung trực của OA nên IO = IA.

FI là đường trung trực của OB nên IO = IB.

Suy ra IO = IA = IB

Xét ∆OIA và ∆OIB có:

OA = OB (giả thiết),

OI là cạnh chung,

IA = IB (chứng minh trên)

Do đó ∆OIA = ∆OIB (c.c.c).

Suy ra ${\hat{O}}_1={\hat{O}}_2$ (hai góc tương ứng).

Do đó OI là tia phân giác của góc xOy.

Vậy OI là tia phân giác của góc xOy.

b) Theo giả thiết OA = OB suy ra O cách đều A và B.

Do đó O nằm trên đường trung trực của đoạn thẳng AB.

Theo chứng minh ở câu a: IA = IB suy ra I cách đều A và B.

Do đó I nằm trên đường trung trực của đoạn thẳng AB.

Vậy OI là đường trung trực của đoạn thẳng AB.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

SBT Toán 7 Bài 8 : Đường vuông góc và đường xiên

SBT Toán 7 Bài 9 : Đường trung trực của một đoạn thẳng

SBT Toán 7 Bài 10 : Tính chất ba đường trung tuyến của tam giác

SBT Toán 7 Bài 11 : Tính chất ba đường phân giác của tam giác

SBT Toán 7 Bài 12 : Tính chất ba đường trung trực của tam giác

Lý thuyết Đường trung trực của một đoạn thẳng

1. Định nghĩa

– Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng ấy.

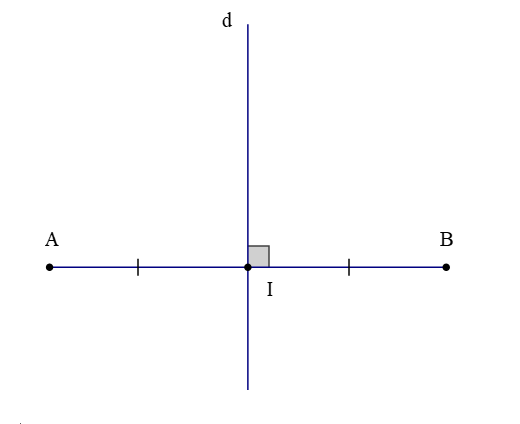
Quan sát hình vẽ trên, ta có:

+ Đoạn thẳng AB; trung điểm I của đoạn thẳng AB;

+ Đường thẳng d ⊥ AB tại I.

Do đó, đường thẳng d là đường trung trực của đoạn thẳng AB.

Ví dụ: Trong các hình dưới đây, hãy chỉ ra các đường trung trực trong mỗi hình (nếu có):

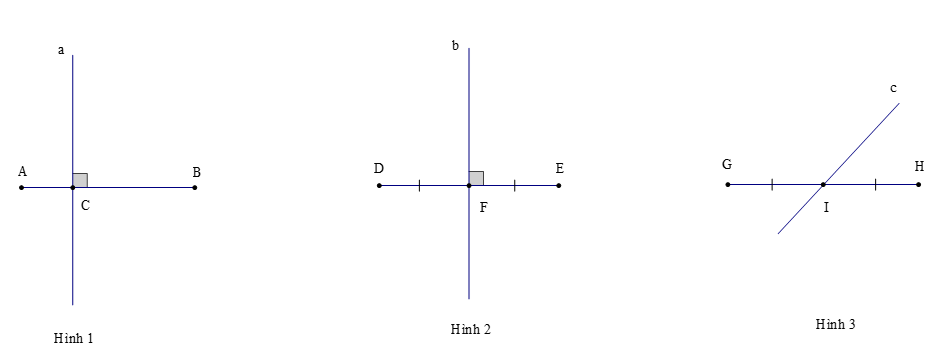
Hướng dẫn giải

– Quan sát hình 1, ta thấy:

Đường thẳng a ⊥ AB tại C nhưng đường thẳng a không đi qua trung điểm của  đoạn thẳng AB.

Do đó, đường thẳng a không là đường trung trực của đoạn thẳng AB.

– Quan sát hình 2, ta thấy:

Đường thẳng b ⊥ DE tại F và đường thẳng b đi qua trung điểm F của đoạn thẳng DE.

Do đó, đường thẳng b là đường trung trực của đoạn thẳng DE.

– Quan sát hình 3, ta thấy:

Đường thẳng c đi qua trung điểm I của đoạn thẳng GH nhưng đường thẳng c không vuông góc với đoạn thẳng GH.

Do đó, đường thẳng c không là đường trung trực của đoạn thẳng GH.

2. Tính chất

– Một điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

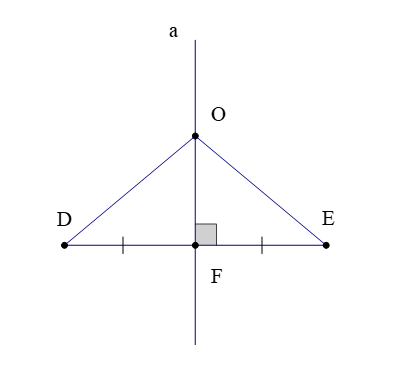
Quan sát hình trên, ta có:

Đường thẳng a là đường trung trực của đoạn thẳng DE;

Điểm O nằm trên đường thẳng a.

Khi đó ta có OD = OE.

Ví dụ: Qua trung điểm O của AB kẻ đường trung trực d. Trên d lấy hai điểm E và F sao cho O nằm giữa E và F. Chứng minh rằng $\widehat{\text{EAF}}=\widehat{\text{EBF}}$.

Hướng dẫn giải

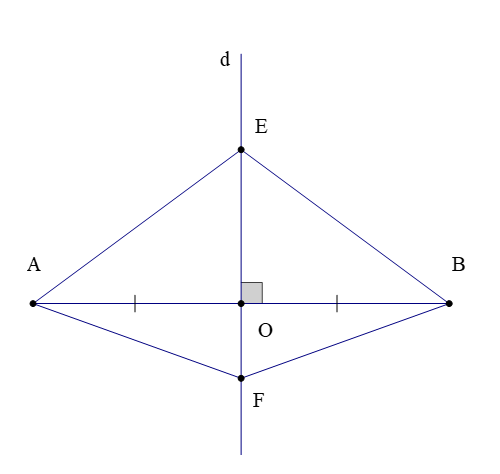
Vì E và F nằm trên đường trung trực d của đoạn thẳng AB (giả thiết)

Nên EA = EB và FA = FB (tính chất đường trung trực)

Xét ∆EAF và ∆EBF ta có:

EA = EB (chứng minh trên),

FA = FB (chứng minh trên),

EF là cạnh chung.

Suy ra ∆EAF = ∆EBF (c.c.c)

Do đó $\widehat{\text{EAF}}=\widehat{\text{EBF}}$(hai góc tương ứng).

Vậy $\widehat{\text{EAF}}=\widehat{\text{EBF}}$.

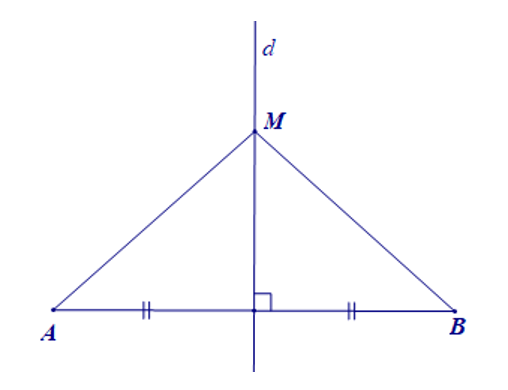
– Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Gọi d là đường trung trực của đoạn thẳng AB, M là điểm sao cho MA = MB (như hình vẽ bên dưới). Ta có M nằm trên đường trung trực d của đoạn thẳng AB.

Ví dụ: Cho ∆ABC cân tại A có $\widehat{\text{BAC}}=80°$, đường trung trực của AB cắt BC tại D. Tính $\widehat{\text{ADB}}.$

Hướng dẫn giải

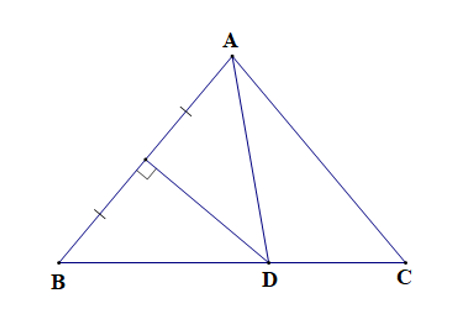
∆ABC cân tại A nên $\widehat{\text{B}}=\widehat{\text{C}}$ (tính chất tam giác cân).

Xét ∆ABC có $\widehat{\text{BAC}}+\widehat{\text{B}}+\widehat{\text{C}}=180°$(tổng ba góc trong một tam giác)

Hay $80°+\widehat{\text{B}}+\widehat{\text{B}}=180°$(vì $\widehat{\text{B}}=\widehat{\text{C}}$)

Suy ra 2$\widehat{\text{B}}=180°-80°=100°$

Suy ra $\widehat{\text{B}}=100°:2=50°.$

Theo bài ta có D nằm trên đường trung trực của AB nên DA = DB.

Suy ra ∆DAB cân tại D.

Do đó $\widehat{\text{B}}=\widehat{\text{BAD}}=50°$ (tính chất tam giác cân)

Xét ∆DAB có: $\widehat{\text{B}}+\widehat{\text{BAD}}+\widehat{\text{ADB}}=180°$(tổng ba góc trong một tam giác)

Hay $\widehat{\text{ADB}}=180°-\widehat{\text{B}}-\widehat{\text{ABD}}=180°-50°-50°=80°$

Vậy $\widehat{\text{ADB}}=80°$.

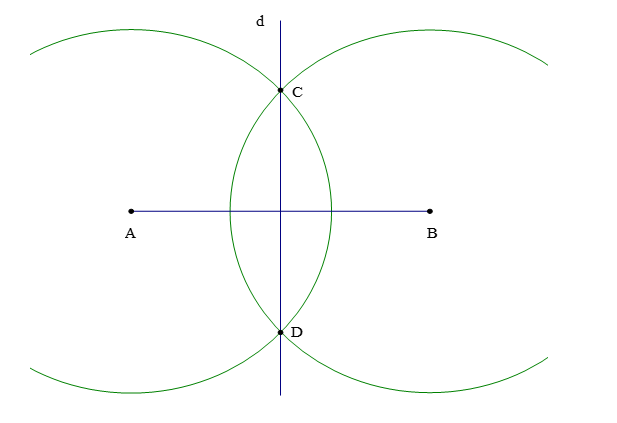
3. Vẽ đường trung trực của một đoạn thẳng

Ví dụ: Dùng thước thẳng (có chia đơn vị) và compa vẽ đường trung trực của đoạn thẳng AB, biết AB = a cm.

Để vẽ đường trung trực của đoạn thẳng AB, ta làm theo các bước:

Bước 1: Vẽ đoạn thẳng AB = a cm.

Bước 2: Vẽ một phần đường tròn tâm A bán kính R (biết R > $\frac{\mathrm{a}}{2}$).

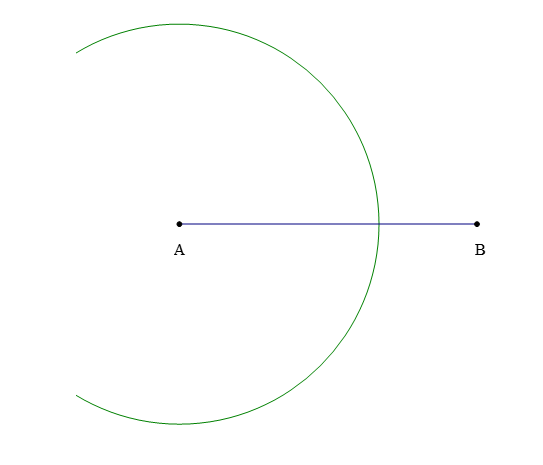
 Bước 3: Vẽ một phần đường tròn tâm B bán kính R (biết R > $\frac{\mathrm{a}}{2}$), cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm C và D.

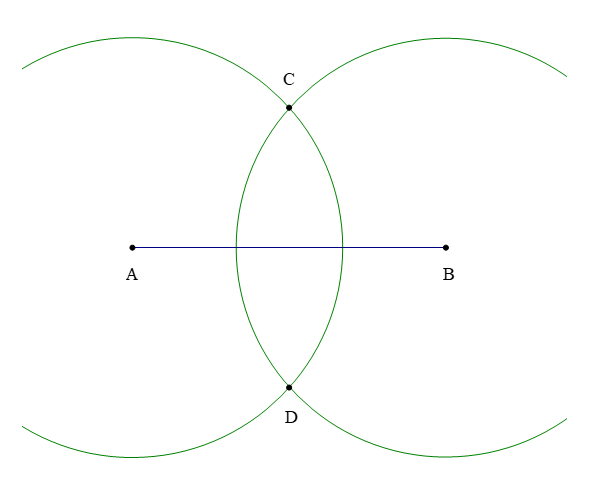
Bước 4: Vẽ đường thẳng đi qua hai điểm C và D. Đường thẳng CD là đường trung trực của đoạn thẳng AB.