Với giải sách bài tập Toán 7 Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh

Giải SBT Toán 7 trang 77 Tập 2

Bài 31 trang 77 sách bài tập Toán lớp 7 Tập 2: Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB > AC. Trong các phát biểu sau, phát biểu nào sai? Vì sao?

a) ΔAED = ΔACB.

b)DE = BC.

c) ΔACE = ΔABD.

d) $\widehat{ABC}=\widehat{A\text{ED}}$ .

Lời giải:

Xét ΔAED và ΔACB có:

$\widehat{DA\text{E}}=\widehat{BAC}$ (cùng bằng 90°),

AD = AB (giả thiết),

AE = AC (giả thiết)

Do đó ΔAED = ΔACB (hai cạnh góc vuông) nên phát biểu a đúng.

Từ ΔAED = ΔACB, suy ra:

• DE = BC (hai cạnh tương ứng), nên phát biểu b đúng.

• $\widehat{ABC}=\widehat{A\text{DE}}$(hai góc tương ứng) nên phát biểu d sai.

Xét ΔACE và ΔABD, ta thấy hai tam giác này không có các cạnh bằng nhau, các góc bằng nhau. Do đó hai tam giác này không bằng nhau, nên phát biểu c sai.

Vậy phát biểu c, d là phát biểu sai.

Giải SBT Toán 7 trang 78 Tập 2

Bài 32 trang 78 sách bài tập Toán lớp 7 Tập 2: Nêu thêm một điều kiện để hai tam giác trong mỗi hình 22a, 22b, 22c, 22d là hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.

a) ∆MAB = ∆MEC (Hình 22a).

b) ∆BAC = ∆DAC (Hình 22b).

c) ∆CAB = ∆DBA (Hình 22c).

d) ∆KDE = ∆NMP (Hình 22d).

Lời giải:

a)

Để ΔMAB = ΔMEC theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen giữa hai cạnh.

Mà tam giác này có $\widehat{AMB}=\widehat{CME}$ (hai góc đối đỉnh) và MB = MC.

Mặt khác $\widehat{AMB}$ là góc xen giữa hai cạnh MA và MB, $\widehat{CME}$ là góc xen giữa hai cạnh MC và ME.

Do đó điều kiện còn lại là điều kiện về cạnh, đó là MA = ME.

Vậy Hình 22a cần thêm điều kiện MA = ME.

b)

ĐểΔBAC = ΔDAC theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen giữa hai cạnh.

Mà hai tam giác này có cạnh AC là cạnh chung, AB = AD.

Mặt khác $\widehat{BAC}$ là góc xen giữa hai cạnh AB và AC, $\widehat{DAC}$ là góc xen giữa hai cạnh AD và AC.

Do đó điều kiện còn lại là điều kiện về góc, đó là $\widehat{BAC}=\widehat{DAC}$ .

Vậy Hình 22b cần thêm điều kiện $\widehat{BAC}=\widehat{DAC}$ .

c)

Để∆CAB = ∆DBA theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen giữa hai cạnh.

Mà hai tam giác này có AB là cạnh chung, $\widehat{BAC}=\widehat{ABD}=90°$ .

Mặt khác $\widehat{BAC}$ là góc xen giữa hai cạnh AB và AC, $\widehat{ABD}$ là góc xen giữa hai cạnh BD và BA.

Do đó điều kiện còn lại là điều kiện về cạnh, đó là AC = BD.

Vậy Hình 22c cần thêm điều kiện AC = BD.

d)

Xét ∆KDE có: $\hat{K}+\hat{D}+\hat{E}=180°$ (tổng ba góc trong một tam giác).

Suy ra $\hat{D}=180°-\hat{K}-\hat{E}=180°-80°-40°=60°$ .

Để∆KDE = ∆NMP theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen giữa hai cạnh.

Mà DK = NM, $\hat{D}=\hat{M}$ (cùng bằng 60°).

Mặt khác $\hat{D}$ là góc xen giữa hai cạnh DK và DE, $\hat{M}$ là góc xen kẽ giữa hai cạnh MN và MP.

Do đó điều kiện còn lại là điều kiện về cạnh, đó là DE = MP.

Vậy Hình 2d cần thêm điều kiện DE = MP.

Bài 33 trang 78 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC. Trên tia đối của tia AB, AC lần lượt lấy các điểm D và E sao cho AD = AB và AE = AC. Gọi M, N lần lượt là trung điểm của BC và DE.

Chứng minh:

a) ∆ABC = ∆ADE;

b) DE = BC và DE song song với BC;

c) ∆AEN = ∆ACM;

d) M, A, N thẳng hàng.

Lời giải:

a) Xét ΔABC và ΔADE có:

AB = AD (giả thiết),

$\widehat{BAC}=\widehat{DA\text{E}}$ (hai góc đối đỉnh),

AC = AE (giả thiết).

Do đó ΔABC = ∆ADE (c.g.c).

Vậy ΔABC = ∆ADE.

b) Vì ∆ABC = ∆ADE (chứng minh câu a)

Suy ra BC = DE (hai cạnh tương ứng), $\widehat{ACB}=\widehat{AED}$(hai góc tương ứng).

Mặt khác $\widehat{ACB},\widehat{AED}$ là hai góc ở vị trí so le trong.

Suy ra DE // BC.

Vậy DE = BC và DE song song với BC.

c) Ta có: $EN=\frac{DE}{2};MC=\frac{BC}{2};DE=BC$ nên EN = MC

Xét ∆AEN và ∆ACM có:

AE = AC(giả thiết),

$\widehat{NEA}=\widehat{MCA}$ (do $\widehat{AED}=\widehat{ACB}$ )

EN = CM (chứng minh trên),

Suy ra ∆AEN = ∆ACM (c.g.c)

Vậy ∆AEN = ∆ACM.

d) Do ∆AEN = ∆ACM (chứng minh câu c).

Nên $\widehat{NAE}=\widehat{MAC}$ (hai góc tương ứng)

Ta có: $\widehat{NAM}=\widehat{NAE}+\widehat{EAM}=\widehat{MAC}+\widehat{EAM}$

Mà $\widehat{MAC}+\widehat{EAM}=\widehat{EAC}=180°$ (hai góc kề bù)

Do đó $\widehat{NAM}={180}^o$

Suy ra M, A, N thẳng hàng

Vậy M, A, N thẳng hàng.

Bài 34 trang 78 sách bài tập Toán lớp 7 Tập 2: >Cho điểm M nằm giữa hai điểm O và A. Vẽ các điểm N và B sao cho O là trung điểm của AB và MN. Vẽ tia Ox vuông góc với AB, trên tia Ox lấy điểm K. Chứng minh:

a) ∆KOM = ∆KON;

b) ∆KMA = ∆KNB.

Lời giải:

a) Xét ∆KOM và ∆KON có:

$\widehat{K\text{O}M}=\widehat{K\text{O}N}$ (cùng bằng 90°),

OK là cạnh chung,

OM = ON (do O là trung điểm của MN).

Suy ra ∆KOM = ∆KON (hai cạnh góc vuông).

Vậy ∆KOM = ∆KON.

b) Do ∆KOM = ∆KON (chứng minh câu a).

Suy ra: $\widehat{KMO}=\widehat{KNO}$ (hai góc tương ứng) và KM = KN (hai cạnh tương ứng).

Ta có OA = OM +MA, OB = ON + NB, OA = OB.

Suy ra MA = NB.

Ta có $\widehat{KMO}+\widehat{KMA}=180°$ (hai góc kề bù) và $\widehat{KNO}+\widehat{KNB}=180°$ (hai góc kề bù).

Mà $\widehat{KMO}=\widehat{KNO}$ (chứng minh trên).

Suy ra $\widehat{KMA}=\widehat{KNB}$ .

Xét ∆KMA và ∆KNB có:

MA = NB (chứng minh trên),

$\widehat{KMA}=\widehat{KNB}$ (chứng minh trên),

KM = KN (chứng minh trên)

Suy ra ∆KMA = ∆KNB (c.g.c).

Vậy ∆KMA = ∆KNB.

Bài 35 trang 78 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có $\widehat{ABC}=53°,\widehat{BAC}=90°$ , AH vuông góc với BC (H thuộc BC). Vẽ tia Bx vuông góc với BC. Trên tia Bx lấy điểm D sao cho BD = HA (Hình 23).

a) Chứng minh ∆AHB = ∆DBH.

b) Chứng minh DH vuông góc với AC.

c) Tính số đo góc BDH.

Lời giải:

a) Xét ∆AHB và ∆DBH có:

$\widehat{AHB}=\widehat{HB\text{D}}$ (cùng bằng 90°),

BH là cạnh chung,

AH = BD (giả thiết),

Suy ra ∆AHB = ∆DBH (hai cạnh góc vuông).

Vậy ∆AHB = ∆DBH.

b) Do ∆AHB = ∆DBH (chứng minh câu a) nên $\widehat{ABH}=\widehat{DHB}$ (hai góc tương ứng).

Mà $\widehat{ABH},\widehat{DHB}$ ở vị trí so le trong

Do đó AB // DH.

Lại có, AB ⊥ AC nên DH ⊥ AC (một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại).

Vậy DH ⊥ AC.

c) Do ∆AHB = ∆DBH (chứng minh câu a) nên $\widehat{BAH}=\widehat{HDB}$ (hai góc tương ứng).

Xét tam giác ABH vuông tại H có:

$\widehat{ABH}+\widehat{BAH}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\widehat{BAH}=90°-\widehat{ABH}=90°-53°=37°$ .

Do đó $\widehat{BDH}=37°$ .

Vậy $\widehat{BDH}=37°$.

Bài 36 trang 78 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có góc A nhỏ hơn 90°. Lấy hai điểm M, N nằm ngoài tam giác ABC sao cho MA vuông góc với AB, NA vuông góc với AC và MA = AB, NA = AC. Gọi I, K lần lượt là giao điểm của BN với AC, MC (Hình 24).

Chứng minh:

a) ∆AMC = ∆ABN;

b) BN vuông góc với CM.

Lời giải:

a) Ta có:

$\widehat{MAC}=\widehat{MAB}+\widehat{BAC}=90°+\widehat{BAC}$

$\widehat{NAB}=\widehat{NAC}+\widehat{BAC}=90°+\widehat{BAC}$

Suy ra: $\widehat{MAC}=\widehat{NAB}$ .

Xét ∆AMC và ∆ABN có:

MA = AB (giả thiết),

$\widehat{MAC}=\widehat{BAN}$ (chứng minh trên),

AC = AN (giả thiết)

Suy ra ∆AMC = ∆ABN (c.g.c).

Vậy ∆AMC = ∆ABN.

b) Do ∆AMC = ∆ABN (chứng minh câu a)

Suy ra $\widehat{ACM}=\widehat{ANB}$ (hai góc tương ứng).

Mặt khác, $\widehat{KIC}+\widehat{AIN}$ (đối đỉnh).

Suy ra $\widehat{ACM}+\widehat{KIC}=\widehat{ANB}+\widehat{AIN}$ .

Xét ∆AIN vuông tại A có: $\widehat{ANI}+\widehat{AIN}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Hay $\widehat{ANB}+\widehat{AIN}={90}^o$

Do đó $\widehat{ACM}+\widehat{KIC}=90°$ hay $\widehat{ICK}+\widehat{KIC}=90°$

Xét ∆KIC, có: $\widehat{ICK}+\widehat{KIC}+\widehat{IKC}=180°$ (tổng ba góc của một tam giác).

Suy ra $\widehat{IKC}=180°-\left(\widehat{ICK}+\widehat{KIC}\right)=180°-90°=90°$ .

Do đó BN ⊥ MC.

Vậy BN ⊥ MC.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

SBT Toán 7 Bài 4 : Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh

SBT Toán 7 Bài 5 : Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh

SBT Toán 7 Bài 6 : Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc

SBT Toán 7 Bài 7 : Tam giác cân

SBT Toán 7 Bài 8 : Đường vuông góc và đường xiên

Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

1. Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)

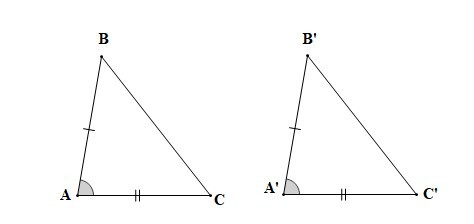
– Tính chất: Nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Nếu AB = A’B’, $\widehat{\mathrm{A}}=\widehat{\mathrm{A}\text{'}}$, AC = A’C’ thì DABC = DA’B’C’ (c.g.c).

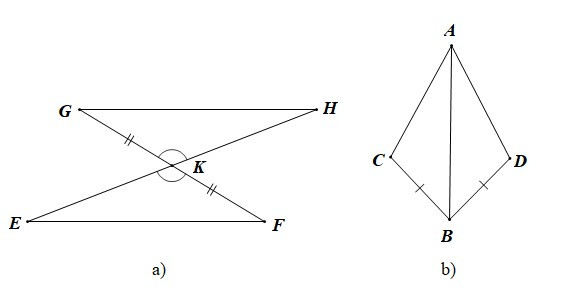
Ví dụ: Biết chỉ cần thêm một điều kiện thì hai tam giác trong mỗi hình dưới đây là hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh. Hãy nêu điều kiện đó tương ứng cho mỗi hình.

Hướng dẫn giải

a) Ta có: $\widehat{\mathrm{GKH}}=\widehat{\mathrm{EKF}}$ (đối đỉnh) và KG = KF.

Để DKGH và DKEF bằng nhau theo trường hợp cạnh – góc – cạnh thì điều kiện còn thiếu là điều kiện về cạnh sao cho cặp góc bằng nhau là góc xen giữa hai cặp cạnh bằng nhau.

Mà $\widehat{\mathrm{GKH}}$ của DKGH xen giữa hai cạnh KG và KH;

$\widehat{\mathrm{EKF}}$ của DKEF xen giữa hai cạnh KE và KF.

Do đó điều kiện còn thiếu là KH = KE.

Vậy điều kiện cần thêm để DKGH = DKFE là KH = KE.

b) Ta có: BC = BD và AB là cạnh chung.

Để DABC và DABD bằng nhau theo trường hợp cạnh – góc – cạnh thì điều kiện còn thiếu là điều kiện về góc sao cho cặp góc bằng nhau là góc xen giữa hai cặp cạnh bằng nhau.

Mà góc xen giữa hai cạnh BC và BA của DABC là $\widehat{\mathrm{ABC}};$

Góc xen giữa hai cạnh BD và BA của DABD là $\widehat{\mathrm{ABD}}.$

Do đó điều kiện còn thiếu là $\widehat{\mathrm{ABC}}=\widehat{\mathrm{ABD}}.$

Vậy điều kiện cần thêm để DABC = DABD là $\widehat{\mathrm{ABC}}=\widehat{\mathrm{ABD}}.$

Ví dụ: Cho tam giác ABC (AB < AC) có tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm E sao cho AB = AE. Chứng minh rằng:

a) DABD = DAED.

b) DA là tia phân giác của $\widehat{\mathrm{BDE}}.$

Hướng dẫn giải

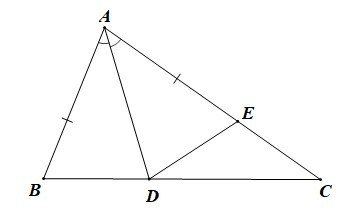
Xét DABD và DAED có:

AB = AE (giả thiết),

$\widehat{\mathrm{BAD}}=\widehat{\mathrm{EAD}}$ (do AD là tia phân giác $\widehat{\mathrm{BAC}}$),

AD là cạnh chung.

Do đó DABD = DAED (c.g.c)

Vậy DABD = DAED (c.g.c).

b) Vì DABD = DAED (chứng minh phần a)

Suy ra $\widehat{\mathrm{BDA}}=\widehat{\mathrm{EDA}}$ (hai góc tương ứng)

Do đó DA là tia phân giác của $\widehat{\mathrm{BDE}}.$

Vậy DA là tia phân giác của $\widehat{\mathrm{BDE}}.$

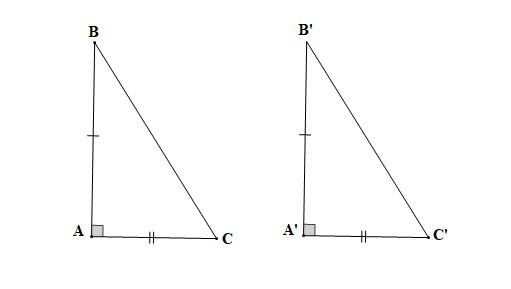
2. Áp dụng vào trường hợp bằng nhau về hai cạnh góc vuông của tam giác vuông

– Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Nếu $\widehat{\mathrm{A}}=\widehat{\mathrm{A}\text{'}}=90°,$AB = A’B’, AC = A’C’ thì DABC = DA’B’C’.

Ví dụ: Cho tam giác ABC có AH ⊥ BC (H ∈ BC) và H là trung điểm của BC. Biết AB = 3 cm. Tính AC.

Hướng dẫn giải

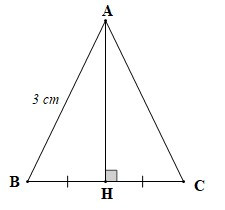
Xét DABH và DACH có:

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{CHA}}=90°$ (giả thiết),

AH là cạnh chung,

BH = CH (giả thiết),

Do đó DABH = DACH (hai cạnh góc vuông).

Suy ra AB = AC (hai cạnh tương ứng) .

Mà AB = 3 cm nên AC = 3 cm.

Vậy độ dài cạnh AC là 3 cm.

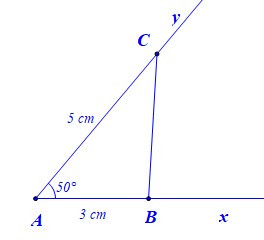
3. Vẽ tam giác khi biết hai cạnh và góc xen giữa

Để vẽ tam giác ABC có AB = 3 cm, AC = 5 cm, $\widehat{\mathrm{A}}=50°$bằng thước thẳng (có chia đơn vị) và thước đo góc, ta làm như sau:

– Bước 1: Vẽ $\widehat{\mathrm{xAy}}=50°$

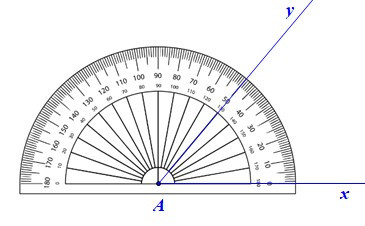
– Bước 2: Trên tia Ax lấy điểm B sao cho AB = 3 cm, trên tia Ay lấy điểm C sao cho AC = 5 cm

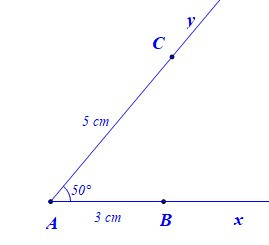
– Bước 3: Vẽ đoạn thẳng BC. Ta được tam giác ABC.