Với giải sách bài tập Toán 7 Bài 5: Phép chia đa thức một biến sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 5: Phép chia đa thức một biến

Giải SBT Toán 7 trang 53 Tập 2

Bài 41 trang 53 sách bài tập Toán lớp 7 Tập 2: Tính:

a) $\left(\frac{3}{4}{x}^3\right):\left(-\frac{1}{2}{x}^2\right)$;

b) (5xⁿ) : (4x²) (n ∈ ℕ, n ≥ 2);

c) $\left(x^3-3x^2+6x\right):\left(-\frac{1}{3}x\right);$

d) $\left(x+\frac{1}{3}{x}^2+\frac{7}{2}{x}^3\right):\left(5x\right).$

Lời giải:

a) $\left(\frac{3}{4}{x}^3\right):\left(-\frac{1}{2}{x}^2\right)$$=\left(\frac{3}{4}:\left(-\frac{1}{2}\right)\right).\left(x^3:x^2\right)$

$=\frac{3}{4}.\frac{-2}{1}.x^{3-2}=-\frac{3}{2}x$;

b) (5xⁿ) : (4x²) = (5 : 4) . (xⁿ – x²) = $\frac{5}{4}$x^{n – 2} (n ∈ℕ, n ≥ 2);

c) $\left(x^3-3x^2+6x\right):\left(-\frac{1}{3}x\right)$

$=\left(x^3:\left(-\frac{1}{3}x\right)\right)-\left(3x^2:\left(-\frac{1}{3}x\right)\right)+\left(6x:\left(-\frac{1}{3}x\right)\right)$

$=\left(1:\left(-\frac{1}{3}\right)\right).\left(x^3:x\right)-\left(3:\left(-\frac{1}{3}\right)\right).\left(x^2:x\right)+\left(6:\left(-\frac{1}{3}\right)\right).\left(x:x\right)$

= 1 . (–3) . x^{3 – 1} – 3 . (–3) . x^{2 – 1} + 6 . (–3) . x^{1 – 1}

= –3x² + 9x – 18;

d) $\left(x+\frac{1}{3}{x}^2+\frac{7}{2}{x}^3\right):\left(5x\right)$

$=\left(x:5x\right)+\left(\frac{1}{3}{x}^2:5x\right)+\left(\frac{7}{2}{x}^3:5x\right)$

$=\left(1:5\right).\left(x:x\right)+\left(\frac{1}{3}:5\right).\left(x^2:x\right)+\left(\frac{7}{2}:5\right).\left(x^3:x\right)$

$=\frac{1}{5}.x^{1-1}+\frac{1}{3}.\frac{1}{5}.x^{2-1}+\frac{7}{2}.\frac{1}{5}.x^{3-1}$

$=\frac{1}{5}{x}^0+\frac{1}{15}{x}^1+\frac{7}{10}{x}^2$

$=\frac{1}{5}+\frac{1}{15}x+\frac{7}{10}{x}^2.$

Bài 42 trang 53 sách bài tập Toán lớp 7 Tập 2:

a) Cho đa thức $P\left(x\right)=\left(6x^5-\frac{1}{2}{x}^4+\frac{1}{3}{x}^3\right):\left(2x^3\right).$ Rút gọn rồi tính giá trị của P(x) tại x = –2.

b) Cho đa thức $Q\left(x\right)=3\left(\frac{2x}{3}-1\right)+\left(15x^2-10x\right):\left(-5x\right)-\left(3x-1\right)$. Rút gọn rồi tính giá trị của Q(x) tại x = $\frac{1}{3}$.

Lời giải:

a) $P\left(x\right)=\left(6x^5-\frac{1}{2}{x}^4+\frac{1}{3}{x}^3\right):\left(2x^3\right)$

$=\left(6x^5:2x^3\right)-\left(\frac{1}{2}{x}^4:2x^3\right)+\left(\frac{1}{3}{x}^3:2x^3\right)$

$=\left(6:2\right).\left(x^5:x^3\right)-\left(\frac{1}{2}:2\right).\left(x^4:x^3\right)+\left(\frac{1}{3}:2\right).\left(x^3:x^3\right)$

$=3.x^{5-3}-\frac{1}{4}.x^{4-3}+\frac{1}{6}.x^{3-3}$

$=3.x^2-\frac{1}{4}.x^1+\frac{1}{6}.x^0$

$=3x^2-\frac{1}{4}x+\frac{1}{6}.$

Thay x = –2 vào $P\left(x\right)=3x^2-\frac{1}{4}x+\frac{1}{6}$ ta được:

$P\left(-2\right)=3.{\left(-2\right)}^2-\frac{1}{4}.\left(-2\right)+\frac{1}{6}=3.4+\frac{1}{2}+\frac{1}{6}$

$=\frac{72+3+1}{6}=\frac{76}{6}=\frac{38}{3}.$

Vậy tại x = –2 thì P(x) có giá trị bằng $\frac{38}{3}.$

b) $Q\left(x\right)=3\left(\frac{2x}{3}-1\right)+\left(15x^2-10x\right):\left(-5x\right)-\left(3x-1\right)$

$=3.\frac{2x}{3}-3.1+\left(15x^2:\left(-5x\right)\right)-\left(10x:\left(-5x\right)\right)-3x+1$

= 2x – 3 + (–3x) – (– 2) – 3x + 1

= [2x + (– 3x) – 3x] + [– 3 – (–2) + 1]

= – 4x.

Thay $x=\frac{1}{3}$ vào Q(x) = – 4x ta được:

$Q\left(\frac{1}{3}\right)=-4.\frac{1}{3}=-\frac{4}{3}.$

Vậy tại $x=\frac{1}{3}$ thì Q(x) có giá trị bằng $-\frac{4}{3}.$

Giải SBT Toán 7 trang 54 Tập 2

Bài 43 trang 54 sách bài tập Toán lớp 7 Tập 2: Khi giải bài tập “Xét xem đa thức A(x) = – 12x⁴ + 5x³ + 15x² có chia hết cho đơn thức B(x) = 3x² hay không”, bạn Hồng nói “Đa thức A(x) không chia hết cho đơn thức B(x) vì 5 không chia hết cho 3”, còn bạn Hà nói “Đa thức A(x) chia hết cho đơn thức B(x) vì số mũ của biến ở mỗi đơn thức của A(x) đều lớn hơn hoặc bằng số mũ của biến đó trong B(x)”. Theo em, bạn nào nói đúng?

Lời giải:

Theo em, bạn Hà nói đúng. Vì:

A(x) : B(x) = (– 12x⁴ + 5x³ + 15x²) : (3x²)

= (– 12x⁴ : 3x²) + (5x³ : 3x²) + (15x² : 3x²)

= –4x² + $\frac{5}{3}$x + 5.

Do đó A(x) ⋮ B(x).

Vậy bạn Hà nói đúng.

Bài 44 trang 54 sách bài tập Toán lớp 7 Tập 2: Tính:

a) (3x³ – 7x² + 4x – 4) : (x – 2);

b) (x⁵ + x + 1) : (x³ – x).

Lời giải:

a) (3x³ – 7x² + 4x – 4) : (x – 2)

Ta thực hiện đặt tính chia đa thức như sau:

Vậy (3x³ – 7x² + 4x – 4) : (x – 2) = 3x² – x + 2.

b) (x⁵ + x + 1) : (x³ – x).

Ta thực hiện đặt tính chia đa thức như sau:

Vậy (x⁵ + x + 1) : (x³ – x) = x³ – x (dư 2x + 1).

Bài 45 trang 54 sách bài tập Toán lớp 7 Tập 2: Cho đa thức P(x) = 3x³ – 2x² + 5. Chia đa thức P(x) cho đa thức Q(x) (Q(x) ≠ 0) được thương là đa thức S(x) = 3x – 2 và dư là đa thức R(x) = 3x + 3. Tìm đa thức Q(x).

Lời giải:

Dựa vào quy tắc phép chia ta có:

P(x) = Q(x) . S(x) + R(x)

Hay P(x) – R(x) = Q(x) . S(x)

Suy ra Q(x) = [P(x) – R(x)] : S(x)

Do đó Q(x) = [(3x³ – 2x² + 5) – (3x + 3)] : (3x – 2)

= (3x³ – 2x² + 5 – 3x – 3) : (3x – 2)

= (3x³ – 2x² – 3x + 2) : (3x – 2)

Ta thực hiện đặt tính chia đa thức như sau:

Khi đó Q(x) = (3x³ – 2x² – 3x + 2) : (3x – 2) = x² – 1.

Vậy Q(x) = x² – 1.

Bài 46 trang 54 sách bài tập Toán lớp 7 Tập 2:

a) Tìm số dư của phép chia đa thức 4x⁴ – 2x² + 7 cho x + 3.

b) Tìm đa thức bị chia, biết đa thức chia là x² – 2x + 3, thương là x² – 2, dư là 9x – 5.

Lời giải:

a) Ta thực hiện đặt tính chia đa thức như sau:

Vậy thực hiện phép chia đa thức 4x⁴ – 2x² + 7 cho x + 3, ta được thương là 4x³ – 12x² + 34x – 102 và số dư là 313.

b) Dựa vào quy tắc phép chia ta có đa thức bị chia là:

(x² – 2x + 3) . (x² – 2) + (9x – 5)

= x² . (x² – 2) – 2x . (x² – 2) + 3 . (x² – 2) + 9x – 5

= x⁴ – 2x² – 2x³ + 4x + 3x² – 6 + 9x – 5

= x⁴ – 2x³ + (– 2x² + 3x²) + (4x + 9x) + (– 6 – 5)

= x⁴ – 2x³ + x² + 13x – 11

Vậy đa thức bị chia cần tìm là x⁴ – 2x³ + x² + 13x – 11.

Bài 47 trang 54 sách bài tập Toán lớp 7 Tập 2:

a) Tìm số a sao cho 10x² – 7x + a chia hết cho 2x – 3.

b) Tìm số a sao cho x³ – 10x + a chia hết cho x – 2.

Lời giải:

a) Ta thực hiện đặt tính chia đa thức như sau:

Do đó số dư của phép chia là a + 12.

Để 10x² – 7x + a chia hết cho 2x – 3 thì số dư bằng 0, tức là a + 12 = 0.

Suy ra a = –12.

Vậy a = –12 thì 10x² – 7x + a chia hết cho 2x – 3.

b) Ta thực hiện đặt tính chia đa thức như sau:

Do đó số dư của phép chia trên là a – 12.

Để x³ – 10x + a chia hết cho x – 2 thì số dư bằng 0, tức là a – 12 = 0.

Suy ra a = 12.

Vậy a = 12 thì x³ – 10x + a chia hết cho x – 2.

Bài 48 trang 54 sách bài tập Toán lớp 7 Tập 2:

Tìm n ∈ ℤ để 2n² – n chia hết cho n + 1.

Lời giải:

Ta thực hiện đặt tính chia đa thức như sau:

Do đó $\frac{2n^2-n}{n+1}=2n-3+\frac{3}{n+1}$ (với n + 1 ≠ 0).

Với n ∈ ℤ để 2n² – n chia hết cho n + 1 thì 3 ⋮ (n + 1).

Điều này xảy ra khi và chỉ khi (n + 1) ∈ Ư(3) = {–1; 1; –3; 3}.

Ta có bảng sau:

Vậy n ∈ {–4; –2; 0; 3}.

Bài 49 trang 54 sách bài tập Toán lớp 7 Tập 2: Một mảnh đất có dạng hình thang vuông với đáy bé là 10 m, chiều cao là 2x + 5 (m). Người ta mở rộng mảnh đất đó để được mảnh đất có dạng hình chữ nhật như Hình 6. Biết diện tích của phần đất mở rộng (phần tô đậm) là 6x² + 13x – 5 (m²), tính diện tích của mảnh đất lúc ban đầu.

Lời giải:

Quan sát Hình 6 ta thấy chiều cao kẻ từ C của tam giác BMC cũng là chiều cao của hình thang vuông AMCD.

Ta có diện tích của tam giác BMC được tính là:

$\frac{1}{2}$ . BM . BC = $\frac{1}{2}$ . BM . (2x + 5) (m²).

Mà theo bài diện tích phần đất dạng tam giác BMC là 6x² + 13x – 5 (m²).

Do đó $\frac{1}{2}$ . BM . (2x + 5) = 6x² + 13x – 5

Hay BM . (2x + 5) = 2 . (6x² + 13x – 5)

Suy ra BM = [2 . (6x² + 13x – 5)] : (2x + 5)

Hay BM = (12x² + 26x – 10) : (2x + 5).

Ta thực hiện đặt tính chia đa thức như sau:

Khi đó BM = 6x – 2 (m).

Suy ra AB = AM + MB = 10 + 6x – 2 = 6x + 8 (m).

Diện tích của mảnh đất hình thang vuông ban đầu là:

$\frac{1}{2}$ . [10 + (6x + 8)] . (2x + 5) = $\frac{1}{2}$ . (6x + 18) . (2x + 5)

= (3x + 9) . (2x + 5) = 3x . (2x + 5) + 9 . (2x + 5)

= 6x² + 15x + 18x + 45 = 6x² + 33x + 45 (m²).

Vậy diện tích của mảnh đất hình thang vuông ban đầu là 6x² + 33x + 45 (m²).

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

SBT Toán 7 Bài 4 : Phép nhân đa thức một biến

SBT Toán 7 Bài 5 : Phép chia đa thức một biến

SBT Toán 7 : Bài tập cuối chương VI 

SBT Toán 7 Bài 1 : Tổng các góc của một tam giác

SBT Toán 7 Bài 2 : Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Lý thuyết Phép chia đa thức một biến

1. Chia đơn thức cho đơn thức

Muốn chia đơn thức A cho đơn thức B (B ≠ 0) khi số mũ của biến trong A lớn hơn hoặc bằng số mũ của biến đó trong B, ta làm như sau:

+ Chia hệ số của đơn thức A cho hệ số của đơn thức B.

+ Chia luỹ thừa của biến trong A cho luỹ thừa của biến đó trong B.

+ Nhân các kết quả vừa tìm được với nhau.

Tổng quát: Với a ≠ 0; b ≠ 0, m, n ∈ ℕ, m ≥ n ta có:

(ax^m) : (bxⁿ) = $\frac{\mathrm{a}}{\mathrm{b}}$.(x^m : xⁿ) = $\frac{\mathrm{a}}{\mathrm{b}}$.x^{m – n}

Ví dụ: Tính:

a) 14x² : 7x;

b) 3x⁶ : 2x²;

c) –5yⁿ : 10y² (với n ∈ ℕ, n > 2);

d) (–20x^{m + 1}) : (5x^{n + 1}) (với m, n ∈ ℕ, m > n).

Hướng dẫn giải

a) 14x² : 7x = (14 : 7). (x² : x) = 2x^{2 – 1} = 2x;

b) 3x⁶ : 2x² = $\frac{3}{2}.$x^{6 – 2} = $\frac{3}{2}.$x⁴;

c) Với n ∈ ℕ, n > 2 ta có:

–5yⁿ : 10y² = $\frac{-5}{10}$.y^{n – 2} = $-\frac{1}{2}$y^{n – 2}.

d) Với m, n ∈ ℕ, m > n ta có:

(–20x^{m + 1}) : (5x^{n + 1})

= (–20 : 5). (x^{m + 1} : x^{n + 1})

= –4x^{m + 1 – n – 1} = –4x^{m – n}.

2. Chia đa thức cho đơn thức

Muốn chia đa thức P cho đơn thức Q (Q ≠ 0) khi số mũ của biến ở mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi đơn thức của đa thức P cho đơn thức Q rồi cộng các thương với nhau.

(A + B) : C = A : C + B : C

(A – B) : C = A : C – B : C

Ví dụ: Tính

a) (20x⁵ – 18x⁴ + 6x² – 4x) : (–2x);

b) (45x⁵ + 10x³ – 5x²) : 5x².

Hướng dẫn giải

a) (20x⁵ – 18x⁴ + 6x² – 4x) : (–2x)

= 20x⁵ : (–2x) – 18x⁴ : (–2x) + 6x² : (–2x) – 4x : (–2x)

= [20 : (–2)](x⁵ : x) – [18 : (–2)](x⁴ : x) + [6 : (–2)](x² : x) – [4 : (–2)](x : x)

= –10x⁴ + 9x³ – 3x + 2.

b) (45x⁵ + 10x³ – 5x²) : 5x²

= 45x⁵ : 5x² + 10x³ : 5x² – 5x² : 5x²

= (45 : 5)(x⁵ : x²) + (10 : 5)(x³ : x²) – (5 : 5)(x² : x²)

= 9x³ + 2x – 1.

3. Chia đa thức một biến đã sắp xếp

* Để chia một đa thức cho một đa thức khác đa thức không (cả hai đa thức đều đã thu gọn và sắp xếp các đơn thức theo số mũ giảm dần của biến) khi bậc của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia, ta làm như sau:

– Bước 1.

+ Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.

+ Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.

+ Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.

– Bước 2. Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức

có bậc nhỏ hơn bậc của đa thức chia.

* Nhận xét

– Khi chia đa thức A cho đa thức B của cùng một biến (B ≠ 0), có hai khả năng xảy ra:

+ Phép chia có dư bằng 0. Trong trường hợp này ta nói đa thức A chia hết cho đa thức B.

+ Phép chia có dư là đa thức R (R ≠ 0) với bậc của R nhỏ hơn bậc của B. Phép chia trong trường hợp này được gọi là phép chia có dư.

– Người ta chứng minh được rằng đối với hai đa thức tuỳ ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B . Q + R, trong đó R bằng 0 hoặc bậc của R nhỏ hơn bậc của B. Như vậy, đã thức A chia hết cho đa thức B khi và chỉ khi R = 0.

Ví dụ: Tính:

a) (9x³ + 6x² + 3x – 3) : (3x + 1)

b) (6x² + 4) : (– 2x – 1)

Hướng dẫn giải

a) Ta thực hiện đặt tính chia đa thức như sau:

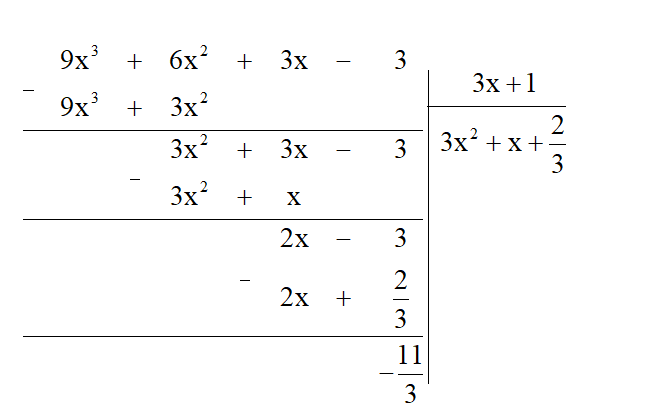
Vậy (9x³ + 6x² + 3x – 3) : (3x + 1) = 3x² + x + $\frac{3}{2}$(dư $\frac{-11}{3}$).

b) Ta thực hiện đặt tính chia đa thức như sau:

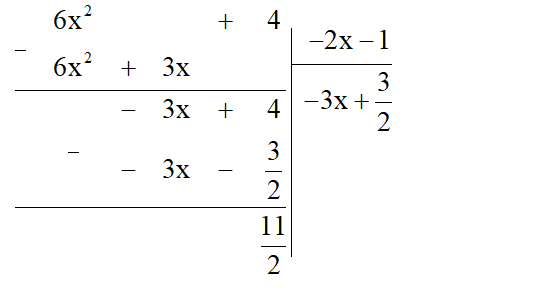
Vậy (6x² + 4) : (–2x – 1) = $-3\text{x}+\frac{3}{2}$ (dư $\frac{11}{2}$).