Với giải sách bài tập Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ
Giải SBT Toán 10 trang 66 Tập 2
Bài 12 trang 66 SBT Toán 10 Tập 2: Cho hai vectơ =(-1;3) và =(2;-5). Tọa độ của vectơ + là:
A. (1; - 2);
B. (- 2; 1);
C. (- 3; 8);
D. (3; - 8).
Lời giải:
Ta có: += ( -1 + 2; 3 + (-5)) = (1; -2).
Vậy chọn đáp án A.
Bài 13 trang 66 SBT Toán 10 Tập 2: Cho hai vectơ =(2;-3) và =(1;4). Tọa độ của vectơ là:
A. (0; 11);
B. (0; - 11);
C. (- 11; 0);
D. (- 3; 10).
Lời giải:
Tọa độ của vectơ = (2-2.1;-3-2.4) = (0;-11)
Vậy chọn đáp án B.
A. (2; 4);
B. (- 3; 3);
C. (3; - 3);
D. (1; 2).
Lời giải:
Tọa độ trung điểm M của đoạn thẳng AB là:
xM= =1
yM= =2
Suy ra M(1; 2)
Vậy chọn đáp án D.
A. ;
B. (8; 4);
C. (2; 4);
D. (4; 2).
Lời giải:
Tọa độ trọng tâm G của tam giác ABC là:
=4
=2
Suy ra G(4; 2)
Vậy chọn đáp án D.
A. ;
B. ;
C. 13;
D. .
Lời giải:
Khoảng cách giữa hai điểm M và N chính bằng độ dài vectơ và bằng
|| =
Vậy chọn đáp án A.
Bài 17 trang 66 SBT Toán 10 Tập 2: Cho hai vectơ =(-4;-3) và =(-1;-7). Góc giữa hai vectơ và là:
A. 900;
B. 600;
C. 450;
D. 300.
Lời giải:
Ta có: cos(;)
=
Suy ra (;)= .
Vậy chọn đáp án C.
Giải SBT Toán 10 trang 67 Tập 2
Bài 18 trang 67 SBT Toán 10 Tập 2: Côsin của góc giữa hai vectơ =(1;1) và =(-2;1) là:
A. ;
B. ;
C. ;
D. .
Lời giải:
Côsin của góc giữa hai vectơ =(1;1) và =(-2;1) là:
cos(;)=
Vậy chọn đáp án C.
A. Tam giác đều;
B. Tam giác vuông tại A;
C. Tam giác có góc tù tại A;
D. Tam giác cân tại A.
Lời giải:
Ta có: =(-2-2;2-6) = (-4;-4) ⇒ AB = || =
=(8-2;0-6) = (6;-6) AC = ||= .
Ta lại có: .= (-4).6+(-4).(-6) = 0
Nên vuông góc với hay tam giác ABC vuông tại A.
Vậy chọn đáp án B.
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm tọa độ trọng tâm G của tam giác ABC.
c) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD=AB.
Lời giải:
a) Ta có: =(-1-1;-1-5)= (-2;-6) và = (2-1;-5-5) = (1;-10)
Ta thấy nên không cùng phương.
Vậy A, B, C không thẳng hàng.
b) Tọa độ trọng tâm G của tam giác ABC:
Vậy .
c) Do tứ giác ABCD là hình thang có AB // CD
Nên và ngược hướng
Mà CD= nên =
Gọi D(a; b), ta có: =(-1-1;-1-5) = (-2;-6), =(a-2b;b+5) .
Suy ra
Vậy D(5; 4).
Lời giải:
Ta có: = (-5+2;-1-4) = (-3;-5)
=(8+2;-2-4) = (10;-6)
=(8+5;-2+1) = (13;-1)
Suy ra: AB=||=
AC=||=
BC=||=
Ta có: .= (-3).10+(-5).(-6) = 0 suy ra vuông góc với hay .
Ta có: cos(,)
= 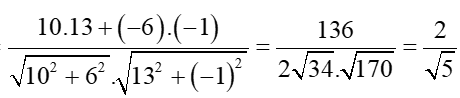
Suy ra .
Lời giải:
Do M nằm trên trục Ox nên M(a; 0).
Khi đó = (4-a;-2) và = (10-a;4).
= (14-2a;2)
||
Suy ra ||2 = (14-2a)2 + 2222=4
Giá trị nhỏ nhất của ||2 là 4
Hay giá trị nhỏ nhất của || là 2 đạt được khi 14 – 2a = 0a=7
Vậy M(7; 0).
Lời giải:
Gọi M(a; b) là tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ.
Ta có: =(a-600;b-200) và =(-400;300)
Do máy bay chuyển động thẳng đều nên quãng đường máy bay đi được sau 1 giờ bằng tổng quãng đường hay AM= AB .
Mà M thuộc đoạn AB nên .
Suy ra
Vậy M .
Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:
SBT Toán 10 Bài 1: Tọa độ của vectơ
SBT Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ
SBT Toán 10 Bài 3: Phương trình đường thẳng
SBT Toán 10 Bài 5: Phương trình đường tròn
Lý thuyết Biểu thức tọa độ của các phép toán vectơ
I. Biểu thức tọa độ của phép cộng hai vectơ, phép trừ hai vectơ, phép nhân một số với một vectơ
Nếu = (x1 ; y1) và = (x2 ; y2) thì
+ = ( x1 + x2 ; y1 + y2);
– = ( x1 – x2 ; y1 – y2);
k = (kx1; ky1) với k ∈ ℝ.
Ví dụ: Cho hai vectơ = (– 5 ; 1) và = (2 ; –3). Tìm tọa độ của mỗi vectơ sau:
a) + ;
b) – ;
c) –2.
Hướng dẫn giải
a) Ta có: + = (–5 + 2 ; 1 + (–3)) = (–3 ; –2).
Vậy + = (–3 ; –2).
b) Ta có – = (–5 – 2 ; 1 – (–3)) = (–7 ; 4).
Vậy – = (–7 ; 4).
c) Ta có –2= (–2.2 ; –2.(–3)) = (–4 ; 6).
Vậy –2= (–4 ; 6).
Nhận xét: Hai vectơ = (x1 ; y1), = (x2 ; y2) ( ≠ ) cùng phương khi và chỉ khi có một số thực k sao cho x1 = kx2 và y1 = ky2.
Ví dụ: Hai vectơ = (–1 ; 2) và = (4 ; –8) có cùng phương hay không?
Hướng dẫn giải
Ta thấy 4 = –4.(–1) và –8 = –4.2
Do đó hai vectơ = (–1 ; 2) và = (4 ; –8) cùng phương với nhau.
Vậy hai vectơ = (–1 ; 2) và = (4 ; –8) cùng phương.
II. Tọa độ trung điểm đoạn thẳng và tọa độ trọng tâm tam giác
– Cho hai điểm A(xA; yA) và B(xB; yB). Nếu M(xM; yM) là trung điểm của đoạn thẳng AB thì
; .
– Cho tam giác ABC có A(xA ; yA), B(xB ; yB), C(xC ; yC). Nếu G(xG ; yG) là trọng tâm của tam giác ABC thì
; .
Ví dụ: Cho tam giác ABC có A(0 ; 3), B(–1 ; –4), C(4 ; –2). Hãy tìm tọa độ trung điểm I của cạnh BC và trọng tâm G của tam giác ABC.
Hướng dẫn giải
Gọi tọa độ trung điểm I của cạnh BC và trọng tâm G của tam giác ABC lần lượt là (xI ; yI) và (xG ; yG).
Khi đó, vì I là trung điểm của BC nên ta có:
; .
Suy ra .
Vì G là trọng tâm của tam giác ABC nên ta có:
; .
Suy ra G(1 ; –1).
Vậy và G(1 ; –1).
III. Biểu thức tọa độ của tích vô hướng
Nếu = (x1; y1) và = (x2; y2) thì .= x1x2 + y1y2.
Nhận xét:
a) Nếu = (x; y) thì .
b) Nếu A(x1; y1) và B(x2; y2) thì AB = = .
c) Với hai vectơ = (x1; y1) và = (x2; y2) đều khác , ta có:
+ và vuông góc với nhau khi và chỉ khi x1x2 + y1y2 = 0.
+ cos(, ) = = .
Ví dụ: Cho hai vectơ ![]() = (3 ; –5) và
= (3 ; –5) và ![]() = (5 ; 3).
= (5 ; 3).
a) Tính  ;
;
b) Tính ![]() .
.![]() ;
;
c) Tính góc giữa hai vectơ ![]() và
và ![]()
Hướng dẫn giải
a) Ta có  =
=  =
= ![]() .
.
Vậy  =
= ![]() .
.
b) Ta có ![]() .
.![]() = 3.5 + (–5).3 = 0.
= 3.5 + (–5).3 = 0.
Vậy ![]() .
.![]() = 0.
= 0.
c) Ta có cos(![]() ,
, ![]() ) =
) =  =
=  =
=  = 0.
= 0.
Suy ra (![]() ,
, ![]() ) = 90°.
) = 90°.
Vậy ![]() và
và ![]() vuông góc với nhau.
vuông góc với nhau.