Giải Toán 8 Bài 3: Rút gọn phân thức

hoa Ngày: 26-09-2022 Lớp 8

3 K

Tailieumoi.vn giới thiệu Giải bài tập Toán 8 Bài 3: Rút gọn phân thức, chi tiết nhất giúp học sinh dễ dàng làm bài tập Rút gọn phân thức lớp 8.

Giải bài tập Toán lớp 8 Bài 3: Rút gọn phân thức

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 38 sgk Toán 8 Tập 1: Cho phân thức: $\frac{4 x^{3}}{10 x^{2} y}$

a) Tìm nhân tử chung của cả tử và mẫu.

b) Chia cả tử và mẫu cho nhân tử chung.

Phương pháp giải: - Phân tích tử và mẫu để tìm nhân tử chung.

- Áp dụng quy tắc chia đơn thức cho đơn thức.

Lời giải:

a) Ta có: $4 x^{3} = 2 x^{2} . 2 x$ và $10 x^{2} . y = 2 x^{2} .5 y$

Nên nhân tử chung của cả tử và mẫu là $2 x^{2}$

b) $\frac{4 x^{3}}{10 x^{2} y} = \frac{4 x^{3} : 2 x^{2}}{10 x^{2} y : 2 x^{2}} = \frac{2 x}{5 y}$

Trả lời câu hỏi 2 trang 38 sgk Toán 8 Tập 1: Cho phân thức: $\frac{5 x + 10}{25 x^{2} + 50 x}$

a) Phân tích tử và mẫu thành nhân tử rồi tìm nhân tử chung của chúng.

b) Chia cả tử và mẫu cho nhân tử chung.

Phương pháp giải: Áp dụng: - Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung.

- Tính chất cơ bản của phân thức.

Lời giải:

a) $5 x + 10 = 5 (x + 2)$

$25 x^{2} + 50 x = 25 x (x + 2)$

$\Rightarrow$ Nhân tử chung của tử và mẫu là: $5 (x + 2)$

$\begin{aligned} \frac{5 x + 10}{25 x^{2} + 50 x} \\ = \frac{(5 x + 10) : [5 (x + 2)]}{(25 x^{2} + 50 x) : [5 (x + 2)]} \\ = \frac{5 (x + 2) : [5 (x + 2)]}{25 x (x + 2) : [5 (x + 2)]} = \frac{1}{5 x} \end{aligned}$

Trả lời câu hỏi 3 trang 38 sgk Toán 8 Tập 1: Rút gọn phân thức: $\frac{x^{2} + 2 x + 1}{5 x^{3} + 5 x^{2}}$

Phương pháp giải: Áp dụng: - Hằng đẳng thức bình phương một tổng.

- Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung.

- Tính chất cơ bản của phân thức.

Lời giải:

$\frac{x^{2} + 2 x + 1}{5 x^{3} + 5 x^{2}} = \frac{{(x + 1)}^{2}}{5 x^{2} (x + 1)} = \frac{x + 1}{5 x^{2}}$

Trả lời câu hỏi 4 trang 38 sgk Toán 8 Tập 1: Rút gọn phân thức: $\frac{3 (x - y)}{y - x}$

Phương pháp giải: Áp dụng tính chất: $A = - (- A)$

Lời giải:

$\frac{3 (x - y)}{y - x} = \frac{- 3 (y - x)}{y - x} = - 3$

Câu hỏi và bài tập (trang 39, 40 sgk Toán 8 Tập 1)

Bài 7 trang 39 sgk Toán 8 Tập 1: Rút gọn phân thức:

a) $\frac{6 x^{2} y^{2}}{8 x y^{5}}$ ; b) $\frac{10 x y^{2} (x + y)}{15 x y (x + y)^{3}}$ ;

c) $\frac{2 x^{2} + 2 x}{x + 1}$ ; d) $\frac{x^{2} - x y - x + y}{x^{2} + x y - x - y}$

Phương pháp giải: - Phân tích tử và mẫu thành nhân tử để tìm nhân tử chung.

- Rút gọn cả tử và mẫu cho nhân tử chung giống nhau.

Lời giải:

a) $\frac{6 x^{2} y^{2}}{8 x y^{5}} = \frac{3 x .2 x y^{2}}{4 y^{3} .2 x y^{2}} = \frac{3 x}{4 y^{3}}$ (rút gọn cho nhân tử chung $2 x y^{2}$ )

b) $\frac{10 x y^{2} (x + y)}{15 x y (x + y)^{3}} = \frac{2 y .5 x y (x + y)}{3 (x + y)^{2} .5 x y (x + y)}$ $= \frac{2 y}{3 (x + y)^{2}}$ (rút gọn cho nhân tử chung $5 x y (x + y)$ )

c) $\frac{2 x^{2} + 2 x}{x + 1} = \frac{2 x (x + 1)}{x + 1} = 2 x$ (rút gọn cho nhân tử chung $x + 1$ )

d) $\frac{x^{2} - x y - x + y}{x^{2} + x y - x - y}$

$= \frac{x (x - y) - (x - y)}{x (x + y) - (x + y)}$

$= \frac{(x - y) (x - 1)}{(x + y) (x - 1)}$

$= \frac{x - y}{x + y}$ (rút gọn cho nhân tử chung $x - 1$ )

Bài 8 trang 40 sgk Toán 8 Tập 1: Trong một tờ nháp của một bạn có ghi một số phép rút gọn phân thức như sau:

a) $\frac{3 x y}{9 y} = \frac{x}{3}$ ;

b) $\frac{3 x y + 3}{9 y + 3} = \frac{x}{3}$ ;

c) $\frac{3 x y + 3}{9 y + 9} = \frac{x + 1}{3 + 3} = \frac{x + 1}{6}$

d) $\frac{3 x y + 3 x}{9 y + 9} = \frac{x}{3}$

Theo em câu nào đúng, câu nào sai? Em hãy giải thích.

Phương pháp giải: Áp dụng tính chất cơ bản của phân thức: Nếu nhân (hoặc chia) cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

Lời giải:

a) $\frac{3 x y}{9 y} = \frac{x .3 y}{3.3 y} = \frac{x}{3}$ , đúng vì đã chia cả tử cả mẫu của vế trái cho $3 y$ .

b) Ta có: $\frac{3 x y + 3}{9 y + 3} = \frac{3 (x y + 1)}{3 (3 y + 1)}$

Xét theo đề bài $\frac{3 x y + 3}{9 y + 3} = \frac{x}{3}$

Mẫu của vế phải là $3$ chứng tỏ đã chia mẫu của vế trái cho $3 y + 1$ vì $9 y + 3 = 3 (3 y + 1)$

Nhưng tử của vế trái không có nhân tử $3 y + 1$ . Nên phép rút gọn này sai.

c) Sai, vì:

$\frac{3 x y + 3}{9 y + 9} = \frac{3 (x y + 1)}{9 (y + 1)} \neq \frac{x + 1}{3 + 3} = \frac{x + 1}{6}$

d) $\frac{3 x y + 3 x}{9 y + 9} = \frac{3 x (y + 1)}{9 (y + 1)} = \frac{x}{3}$

Đúng, vì đã chia cả tử và mẫu của phân thức cho $3 (y + 1) .$

Bài 9 trang 40 sgk Toán 8 Tập 1: Áp dụng quy tắc đổi dấu rồi rút gọn phân thức:

a) $\frac{36 (x - 2)^{3}}{32 - 16 x}$ ;

b) $\frac{x^{2} - x y}{5 y^{2} - 5 x y}$

Phương pháp giải: - Áp dụng qui tắc đối dấu: $\frac{A}{B} = \frac{- A}{- B}$

- Phân tích tử và mẫu thành nhân tử để tìm nhân tử chung

- Rút gọn cả tử và mẫu cho nhân tử chung giống nhau.

Lời giải:

a) $\frac{36 (x - 2)^{3}}{32 - 16 x} = \frac{36 (x - 2)^{3}}{16 (2 - x)}$

$= \frac{36 (x - 2)^{3}}{- 16 (x - 2)} = \frac{- 9 (x - 2)^{2} .4 (x - 2)}{4.4 (x - 2)}$ $= \frac{- 9 (x - 2)^{2}}{4}$

Cách 2:

$\frac{36 (x - 2)^{3}}{32 - 16 x} = \frac{36 (x - 2)^{3}}{16 (2 - x)}$

$= \frac{36 [- (2 - x)]^{3}}{16 (x - 2)} = \frac{- 36 (2 - x)^{3}}{16 (2 - x)}$

$= \frac{- 9 (2 - x)^{2} .4 (2 - x)}{4.4 (2 - x)} = \frac{- 9 (2 - x)^{2}}{4}$

b) $\frac{x^{2} - x y}{5 y^{2} - 5 x y} = \frac{x (x - y)}{5 y (y - x)}$

$= \frac{- x (y - x)}{5 y (y - x)} = \frac{- x}{5 y}$

Bài 10 trang 40 sgk Toán 8 Tập 1: Đố em rút gọn được phân thức:

$\frac{x^{7} + x^{6} + x^{5} + x^{4} + x^{3} + x^{2} + x + 1}{x^{2} - 1}$

Phương pháp giải: - Trên tử số: ta nhóm các hạng tử để xuất hiện nhân tử chung rồi phân tích thành nhân tử.

- Dưới mẫu số: áp dụng hằng đẳng thức hiệu hai bình phương để phân tích thành nhân tử.

- Chia cả tử và mẫu cho nhân tử chung giống nhau.

Lời giải:

$\frac{x^{7} + x^{6} + x^{5} + x^{4} + x^{3} + x^{2} + x + 1}{x^{2} - 1}$

$= \frac{(x^{7} + x^{6}) + (x^{5} + x^{4}) + (x^{3} + x^{2}) + (x + 1)}{(x - 1) (x + 1)}$

$= \frac{x^{6} (x + 1) + x^{4} (x + 1) + x^{2} (x + 1) + (x + 1)}{(x - 1) (x + 1)}$

$= \frac{(x + 1) (x^{6} + x^{4} + x^{2} + 1)}{(x - 1) (x + 1)}$

$= \frac{x^{6} + x^{4} + x^{2} + 1}{x - 1}$

Bài 11 trang 40 sgk Toán 8 Tập 1: Rút gọn phân thức:

a) $\frac{12 x^{3} y^{2}}{18 x y^{5}}$ ; b) $\frac{15 x {(x + 5)}^{3}}{20 x^{2} (x + 5)}$

Phương pháp giải: - Phân tích tử và mẫu thành nhân tử để tìm nhân tử chung

- Rút gọn cả tử và mẫu cho nhân tử chung giống nhau.

Lời giải:

a) $\frac{12 x^{3} y^{2}}{18 x y^{5}} = \frac{2 x^{2} .6 x y^{2}}{3 y^{3} .6 x y^{2}} = \frac{2 x^{2}}{3 y^{3}}$ (rút gọn cho nhân tử chung $6 x y^{2})$

b) $\frac{15 x {(x + 5)}^{3}}{20 x^{2} (x + 5)} = \frac{3 {(x + 5)}^{2} .5 x (x + 5)}{4 x .5 x (x + 5)}$ $= \frac{3 {(x + 5)}^{2}}{4 x}$ (rút gọn cho nhân tử chung $5 x (x + 5))$

Bài 12 trang 40 sgk Toán 8 Tập 1: Phân tích tử và mẫu thành nhân tử rồi rút gọn phân thức:

a) $\frac{3 x^{2} - 12 x + 12}{x^{4} - 8 x}$ ;

b) $\frac{7 x^{2} + 14 x + 7}{3 x^{2} + 3 x}$

Phương pháp giải: - Phân tích tử và mẫu thành nhân tử bằng phương pháp dùng hằng đẳng thức để tìm nhân tử chung

- Rút gọn cả tử và mẫu cho nhân tử chung giống nhau.

Lời giải:

$\begin{aligned} \frac{3 x^{2} - 12 x + 12}{x^{4} - 8 x} = \frac{3 (x^{2} - 4 x + 4)}{x (x^{3} - 8)} \\ = \frac{3 (x^{2} - 2. x .2 + 2^{2})}{x (x^{3} - 2^{3})} \\ = \frac{3 {(x - 2)}^{2}}{x (x - 2) (x^{2} + 2 x + 4)} \\ = \frac{3 (x - 2)}{x (x^{2} + 2 x + 4)} \end{aligned}$

$\begin{aligned} \frac{7 x^{2} + 14 x + 7}{3 x^{2} + 3 x} = \frac{7 (x^{2} + 2 x + 1)}{3 x (x + 1)} \\ = \frac{7 {(x + 1)}^{2}}{3 x (x + 1)} = \frac{7 (x + 1)}{3 x} \end{aligned}$

(rút gọn cho nhân tử chung là $x + 1)$

Bài 13 trang 40 sgk Toán 8 Tập 1: Áp dụng quy tắc đổi dấu rồi rút gọn phân thức:

a) $\frac{45 x (3 - x)}{15 x {(x - 3)}^{3}}$ ; b) $\frac{y^{2} - x^{2}}{x^{3} - 3 x^{2} y + 3 x y^{2} - y^{3}}$

Phương pháp giải: - Áp dụng quy tắc đổi dấu.

- Phân tích tử và mẫu thành nhân tử để tìm nhân tử chung.

- Chia cả tử và mẫu cho nhân tử chung giống nhau.

Lời giải:

$\begin{aligned} \frac{45 x (3 - x)}{15 x {(x - 3)}^{3}} = \frac{3.15 x (3 - x)}{15 x {(x - 3)}^{3}} \\ = \frac{3 (3 - x)}{{(x - 3)}^{3}} = \frac{- 3 (x - 3)}{{(x - 3)}^{3}} \\ = \frac{- 3. (x - 3)}{{(x - 3)}^{2} . (x - 3)} \\ = \frac{- 3}{{(x - 3)}^{2}} \end{aligned}$

$\begin{aligned} \frac{y^{2} - x^{2}}{x^{3} - 3 x^{2} y + 3 x y^{2} - y^{3}} \\ = \frac{(y + x) (y - x)}{{(x - y)}^{3}} \\ = \frac{- (x + y) (x - y)}{{(x - y)}^{3}} (do y - x = - (x - y)) \\ = \frac{- (x + y)}{{(x - y)}^{2}} \end{aligned}$

Lý thuyết rút gọn phân thức

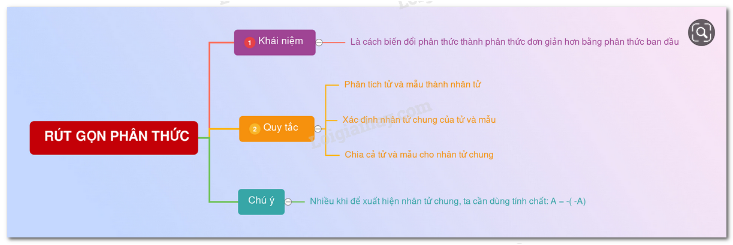
1. Rút gọn phân thức đại số: Cách biến đổi phân thức thành phân thức đơn giản hơn và bằng phân thức đã cho gọi là rút gọn phân thức.

- Muốn rút gọn một phân thức ta có thể làm như sau:

+ Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.

+ Chia cả tử và mẫu cho nhân tử chung (nếu có).

Chú ý:

Nhiều khi ta cần đổi dấu ở tử hoặc mẫu để nhận ra nhân tử chung của tử và mẫu bằng việc sử dụng tính chất:

Ví dụ: $\frac{20 x^{2} - 45}{{(2 x - 3)}^{2}} = \frac{5 (4 x^{2} - 9)}{{(2 x - 3)}^{2}} = \frac{5 (2 x - 3) (2 x + 3)}{{(2 x - 3)}^{2}} = \frac{5 (2 x + 3)}{2 x - 3} .$