Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài tập cuối chương 4 chi tiết sách Toán 7 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài tập cuối chương 4
Bài 1 trang 108 Toán lớp 7: a) Cho một ví dụ về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.
b) Thế nào là tia phân giác của một góc?
c) Cho một ví dụ về hai góc đồng vị, hai góc so le trong.
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có bằng nhau không? Hai góc so le trong có bằng nhau hay không?
e) Phát biểu tiên đề Euclid về đường thẳng song song.
Phương pháp giải:
+ Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
+ 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
+ 2 góc có tổng số đo là 180 độ là 2 góc bù nhau
+ 2 góc kề bù nếu chúng vừa kề nhau, vừa bù nhau
+ Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
+ 1 đường thẳng cắt 2 đường thẳng song song tạo ra các cặp góc so le trong bằng nhau, đồng vị bằng nhau.
+ Tiên đề Euclid về đường thẳng song song.
Lời giải:
a)
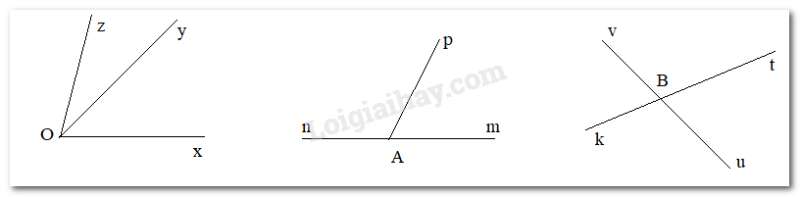
+ Ví dụ về 2 góc kề nhau: Góc xOy và góc yOz
+ Ví dụ về 2 góc kề bù: góc mAp và pAn
+ Ví dụ về hai góc đối đỉnh: góc uBt và góc vBk
b) Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
c)
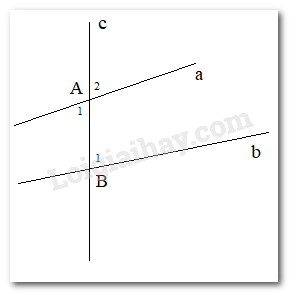
Đường thẳng c cắt hai đường thẳng a và b, tạo ra: Góc A1 và B1 là cặp góc so le trong; Góc A2 và B1 là cặp góc đồng vị
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau; hai góc so le trong bằng nhau ( Tính chất 2 đường thẳng song song)
e) Tiên đề Euclide về đường thẳng song song: Qua 1 điểm nằm ngoài đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
Bài 2 trang 108 Toán lớp 7: a) Hai góc có tổng số đo bằng 180 có phải là hai góc kề bù hay không?
b) Hai góc bằng nhau và có chung đỉnh có phải là hai góc đối đỉnh hay không?
Phương pháp giải:
Chỉ ra một ví dụ chứng tỏ khẳng định sai
Lời giải:
a) Hai góc có tổng số đo bằng 180 không phải là hai góc kề bù, vì 2 góc kề bù phải là 2 góc kề nhau và có tổng số đo bằng 180 , chẳng hạn:
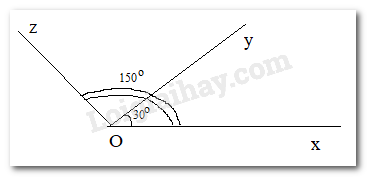
Góc xOy và góc xOz có tổng số đo bằng 180 nhưng không phải là hai góc kề bù, vì không kề nhau
b) Hai góc bằng nhau và có chung đỉnh không phải là hai góc đối đỉnh, chẳng hạn:
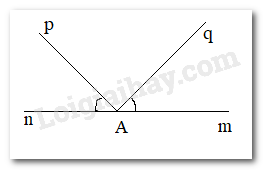
Góc mAq và nAp bằng nhau và có chung đỉnh nhưng không phải là hai góc đối đỉnh.
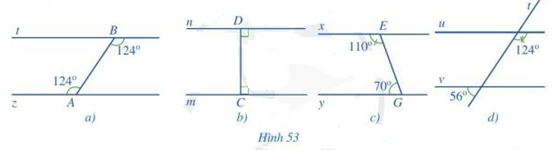
Phương pháp giải:
+ Sử dụng dấu hiệu nhận biết 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ 2 góc kề bù có tổng số đo là 180 độ
Lời giải:
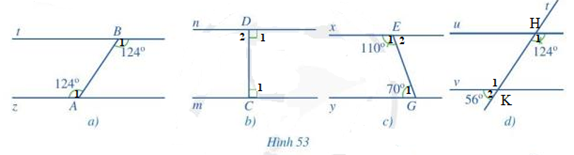
a) Vì . Mà 2 góc này ở vị trí so le trong nên z // t
b) Vì ( 2 góc kề bù) nên
Vì . Mà 2 góc này ở vị trí so le trong nên m // n
c) Vì ( 2 góc kề bù) nên
Vì . Mà 2 góc này ở vị trí so le trong nên x //y
d) Vì ( 2 góc kề bù) nên
Vì . Mà 2 góc này ở vị trí so le trong nên x //y
a) Tính số đo góc BCx.
b) Chứng minh rằng Cx song song với DE.
c) Tính số đo góc BCD.
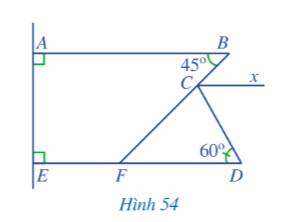
Phương pháp giải:
+ Sử dụng dấu hiệu nhận biết 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ Chú ý: 2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau
2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau
+ Sử dụng tính chất 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
+ Nếu tia Om nằm trong góc xOy thì
Lời giải:
|
GT |
AB ⊥ AE tại A, DE ⊥ AE tại E, Cx // AB, BC cắt DE tại F |
|
KL |
a) b) Cx // DE. c) |
a) Vì Cx // AB (GT) nên (hai góc so le trong)
Mà (GT)
Do đó
b) Vì AB ⊥ AE nên
Vì nên
Khi đó,
Mà và là hai góc trong cùng phía.
Suy ra AB // DE (dấu hiệu nhận biết)
Do đó (hai góc so le trong)
Suy ra
Mà hai góc và ở vị trí so le trong
Nên Cx // DE (dấu hiệu nhận biết).
b) Theo câu b: Cx // DE nên (hai góc so le trong).
Vì tia Cx nằm giữa hai tia CB và CD nên:
Vậy
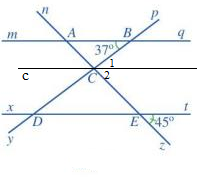
Bài 5 trang 108 Toán lớp 7: Quan sát Hình 55, trong đó mq // xt
a) Kể tên các cặp góc đồng vị bằng nhau.
b) Tìm số đo các góc BAC, CDE.
c) Bạn Nam cho rằng: Qua điểm C kẻ một đường thẳng c song song với hai đường thẳng mq và xt thì sẽ tính được . Theo em, bạn Nam nói đúng hay sai? Vì sao?
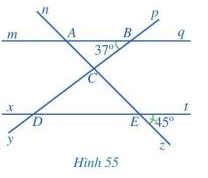
Phương pháp giải:
+ 2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau
+ Sử dụng tính chất 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
+ Nếu tia Om nằm trong góc xOy thì
Lời giải:
a) Các cặp góc đồng vị bằng nhau là: góc mAn và xEn; góc mAz và xEz; góc nAq và nEt; góc qAz và tEz; góc pBq và pDt; góc qBy và tDy; góc mBy và xDy; góc pBm và pDx
b) Vì ( 2 góc đối đỉnh) nên
Mà mq // xt nên ( 2 góc so le trong)
c)
Bạn Nam nói đúng vì:
Vì c // mq nên ( 2 góc so le trong) nên
Vì c // xt nên ( 2 góc so le trong) nên
Vì nên
Lý thuyết Toán 7 Chương 4: Góc. Đường thẳng song song
1. Góc ở vị trí đặc biệt
1.1 Hai góc kề nhau
Hai góc kề nhau là hai góc có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.
Tính chất:
- Cho góc xOz (khác góc bẹt) và tia Oy nằm trong góc đó. Khi đó hai góc xOy và yOz là hai góc kề nhau và .
- Nếu góc xOz là góc bẹt thì với mỗi tia Oy (khác hai tia Ox, Oz), ta cũng có: .
1.2 Hai góc bù nhau. Hai góc kề bù
- Hai góc bù nhau là hai góc có tổng bằng 180°.
- Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù.
Chú ý: Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau là hai góc kề bù.
1.3 Hai góc đối đỉnh
- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
- Hai góc đối đỉnh thì bằng nhau.
2. Tia phân giác của một góc
2.1 Định nghĩa
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
2.2 Vẽ tia phân giác của một góc
Cho góc xOy. Để vẽ tia phân giác của góc xOy ta có các cách sau:
Cách 1: Vẽ tia phân giác của một góc bằng thước thẳng và compa.
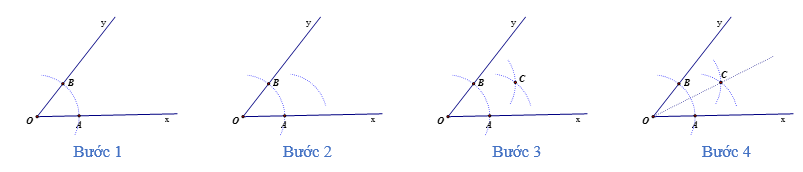
Bước 1: Trên tia Ox lấy điểm A bất kì (A khác O). Vẽ một phần đường tròn tâm O bán kính OA, cắt tia Oy tại điểm B.
Bước 2: Vẽ một phần đường tròn tâm A bán kính AO.
Bước 3: Vẽ một phần đường tròn tâm B bán kính AO, cắt phần đường tròn tâm A bán kính AO tại điểm C nằm trong góc xOy.
Bước 4: Vẽ tia OC, ta được tia phân giác của góc xOy.
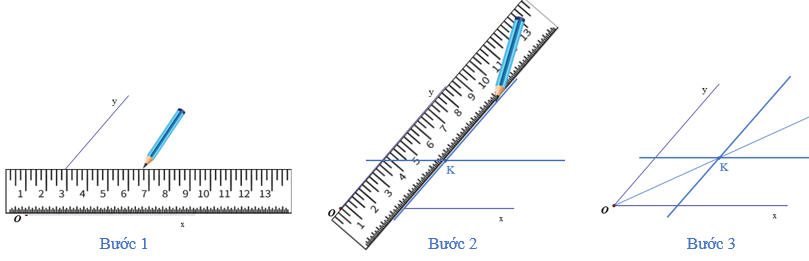
Cách 2: Dùng thước hai lề
Bước 1: Đặt thước hai lề sao cho một cạnh của thước trùng với một trong hai cạnh của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.
Bước 2: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh còn lại của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.
Bước 3: Hai nét vạch ở bước 1 và bước 2 cắt nhau tại điểm K nằm trong góc xOy. Vẽ tia OK, ta được tia này là tia phân giác của góc xOy.
3. Hai đường thẳng song song
3.1 Hai góc đồng vị. Hai góc so le trong

Đường thẳng c cắt hai đường thẳng a, b lần lượt tại điểm A, B.
Khi đó, ta thấy:
+ Góc A1 và góc B1 ở “cùng một phía” của đường thẳng c.
+ Góc A1 ở “phía trên” đường thẳng a. Góc B1 cũng ở “phía trên” đường thẳng b.
Hai góc A1 và B1 ở vị trí như thế được gọi là hai góc đồng vị.
 + Góc A3 và góc B1 ở “hai phía” của đường thẳng c.
+ Góc A3 và góc B1 ở “hai phía” của đường thẳng c.
+ Góc A3 ở “phía dưới” của đường thẳng a. Góc B1 lại ở “phía trên” của đường thẳng b.
Hai góc A3 và B1 ở vị trí như thế gọi là hai góc so le trong.
3.2 Dấu hiệu nhận biết hai đường thẳng song song
- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a và b song song với nhau.
Nhận xét: Qua một điểm ở ngoài một đường thẳng luôn có một đường thẳng song song với đường thẳng đó.
3.3 Tiên đề Euclid về đường thẳng song song
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Nhận xét: Nếu hai đường thẳng cùng đi qua điểm M và cùng song song song với đường thẳng a (M ∉ a) thì hai đường thẳng đó trùng nhau.
3.4 Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
- Hai góc đồng vị bằng nhau.
- Hai góc so le trong bằng nhau.
Chú ý: Nếu đường thẳng c cắt hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau.
+ Hai góc trong cùng phía có tổng số đo bằng 1800.
4. Định lý
4.1 Định lí
Khẳng định có các tính chất sau thì được gọi là định lý:
- Là một phát biểu về một tính chất toán học;
- Tính chất toán học đó đã được chứng tỏ là đúng không dựa vào trực giác hay đo đạc,..
Nhận xét:
+ Định lý thường được phát biểu dưới dạng “Nếu … thì …”.
+ Phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết, phần nằm sau từ “thì” là phần kết luận.
4.2 Chứng minh định lý
Chứng minh định lý là một tiến trình lập luận từ giả thiết suy ra kết luận là đúng.
Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:
Bài 2: Tia phân giác của một góc