Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 3: Hai đường thẳng song song chi tiết sách Toán 7 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 3: Hai đường thẳng song song
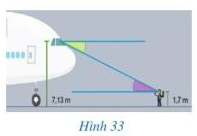
Theo em dự đoán, hai góc đó có bằng nhau hay không?
Phương pháp giải:
Ước lượng số đo 2 góc
Lời giải:
Dự đoán: góc quan sát của người phi công và góc quan sát của người hoa tiêu khi hướng dẫn máy bay vào vị trí sân bay bằng nhau.
I. Hai góc đồng vị. Hai góc so le trong
II. Dấu hiệu nhận biết hai đường thẳng song song
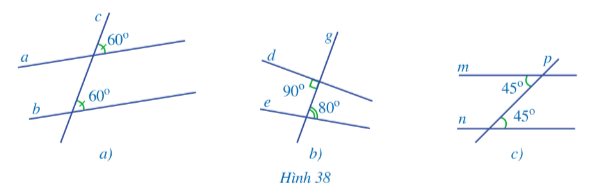
Lời giải:
- Hình 38a: Gọi giao điểm của đường thẳng a, b với đường thẳng c lần lượt là hai điểm A và B (như hình vẽ).
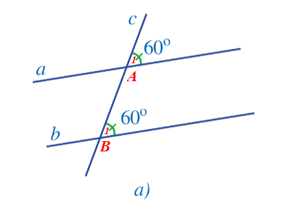
Nhận thấy: và và ở vị trí đồng vị.
Dự đoán: Đường thẳng a song song với đường thẳng b.
- Hình 38b: Gọi giao điểm của đường thẳng d, e với đường thẳng g lần lượt là hai điểm D và E (như hình vẽ).
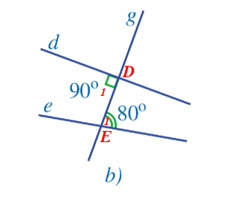
Nhận thấy: nên và và ở vị trí so le trong.
Dự đoán: Đường thẳng d không song song với đường thẳng e.
- Hình 38c: Gọi giao điểm của đường thẳng m, n với đường thẳng p lần lượt là hai điểm M và N (như hình vẽ).
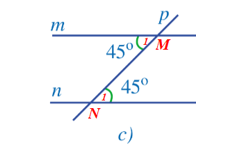
Nhận thấy: và và ở vị trí so le trong.
Dự đoán: Đường thẳng m song song với đường thẳng n.
b) Giải thích vì sao đường thẳng b song song với đường thẳng a
Phương pháp giải:
Sử dụng dấu hiệu nhận biết 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
Lời giải:
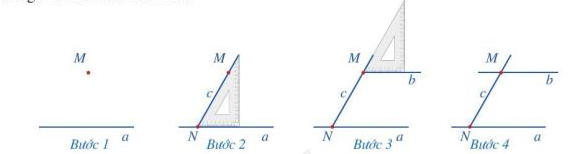
a) Thực hiện vẽ hình theo các bước đã nêu ở đề bài.
b) Đường thẳng b song song với đường thẳng a vì đường thẳng c cắt 2 đường thẳng a và b tạo ra một cặp góc đồng vị bằng nhau
III. Tiên đề Euclid về đường thẳng song song
IV. Tính chất của hai đường thẳng song song
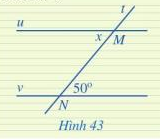
Luyện tập vận dụng trang 103 Toán lớp 7: Tìm số đo x trong Hình 43, biết u // v
Phương pháp giải:
Sử dụng tính chất: Đường thẳng c cắt 2 đường thẳng song song, tạo thành 1 cặp góc so le trong bằng nhau.
Lời giải:
Vì u // v nên x = 50 ( 2 góc so le trong)
Bài 1 trang 104 Toán lớp 7: Quan sát hình 44, biết a // b.
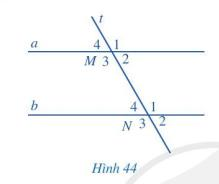
a) So sánh và ; và ( mỗi cặp góc M1 và N3, M4 và N2 gọi là một cặp góc so le ngoài)
b) Tính: và ( mỗi cặp góc M2 và N1, M3 và N4 gọi là một cặp góc trong cùng phía)
Phương pháp giải:
+ 1 đường thẳng cắt 2 đường thẳng song song tạo ra các cặp góc so le trong bằng nhau, đồng vị bằng nhau.
+ 2 góc đối đỉnh thì bằng nhau.
+ 2 góc kề bù có tổng số đo bằng 180
Lời giải:
a) Vì a // b nên ; ( 2 góc đồng vị) mà ; ( 2 góc đối đỉnh) nên =; =
b) Vì a // b nên ( 2 góc đồng vị), mà ( 2 góc kề bù) nên = 180; = 180
Chú ý:
Nếu đường thẳng c cắt cả hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau
+ Hai góc trong cùng phía có tổng số đo bằng 180
Bài 2 trang 104 Toán lớp 7: Quan sát Hình 45.
a) Vì sao hai đường thẳng a và b song song với nhau?
b) Tính số đo góc BCD.
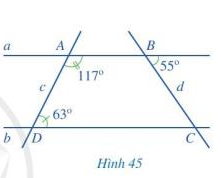
Phương pháp giải:
+ Sử dụng tính chất: Hai góc kề bù có tổng số đo bằng 180 độ
+ Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong bằng nhau hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ Sử dụng tính chất: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
Lời giải:
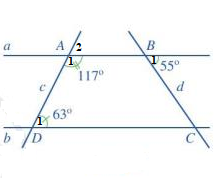
a) Vì ( 2 góc kề bù) nên
Vì ( cùng bằng 63 độ)
Mà 2 góc này ở vị trí đồng vị
a // b ( đpcm)
b) Vì a // b nên ( 2 góc so le trong), mà
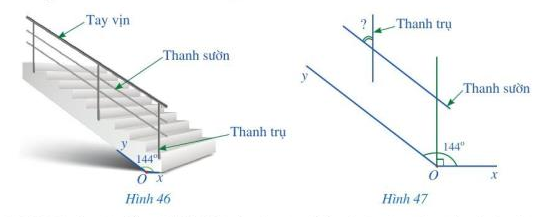
Trong Hình 46, góc xOy bằng 144. Hỏi góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can là bao nhiêu độ?
Phương pháp giải:
Sử dụng tính chất: + Hai góc kề bù có tổng số đo bằng 180 độ
+ Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
Lời giải:
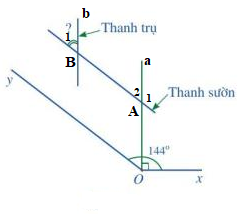
Vì AB // Oy nên ( 2 góc đồng vị), mà
Vì ( 2 góc kề bù) nên
Vì a // b nên ( 2 góc đồng vị), mà .
Lý thuyết Hai đường thẳng song song
1. Hai góc đồng vị. Hai góc so le trong

Đường thẳng c cắt hai đường thẳng a, b lần lượt tại điểm A, B.
Khi đó, ta thấy:
+ Góc A1 và góc B1 ở “cùng một phía” của đường thẳng c.
+ Góc A1 ở “phía trên” đường thẳng a. Góc B1 cũng ở “phía trên” đường thẳng b.
Hai góc A1 và B1 ở vị trí như thế được gọi là hai góc đồng vị.
 + Góc A3 và góc B1 ở “hai phía” của đường thẳng c.
+ Góc A3 và góc B1 ở “hai phía” của đường thẳng c.
+ Góc A3 ở “phía dưới” của đường thẳng a. Góc B1 lại ở “phía trên” của đường thẳng b.
Hai góc A3 và B1 ở vị trí như thế gọi là hai góc so le trong.
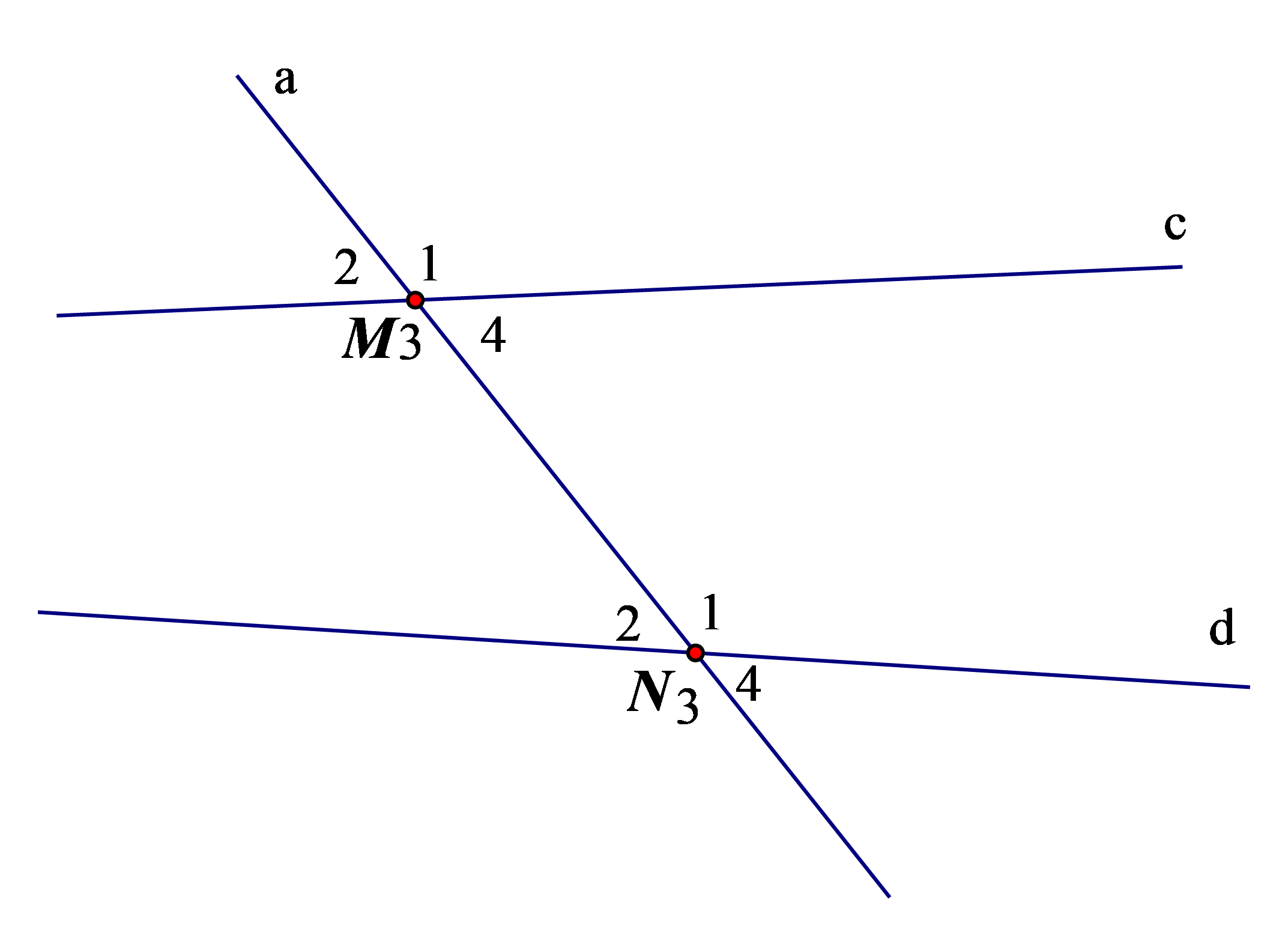
Ví dụ: Kể tên các cặp góc so le trong và đồng vị trong hình sau:
 Hướng dẫn giải
Hướng dẫn giải
Các cặp góc so le trong là: M3 và N1; M4 và N2.
Các cặp góc đồng vị là: M1 và N1; M2 và N2; M3 và N3; M4 và N4.
2. Dấu hiệu nhận biết hai đường thẳng song song
- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a và b song song với nhau.
Ví dụ:
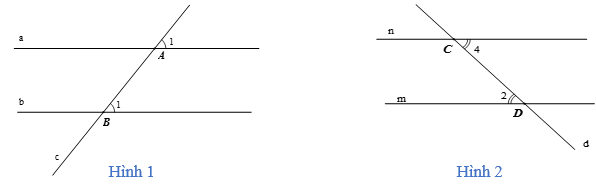
- Ở hình 1: Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau nên a // b.
- Ở hình 2: Đường thẳng d cắt hai đường thẳng m, n và trong các góc tạo thành có một cặp góc so le trong bằng nhau nên m // n.
Ví dụ: Vẽ một đường thẳng b đi qua điểm M và song song với đường thẳng a (M ∉ a) bằng êke.
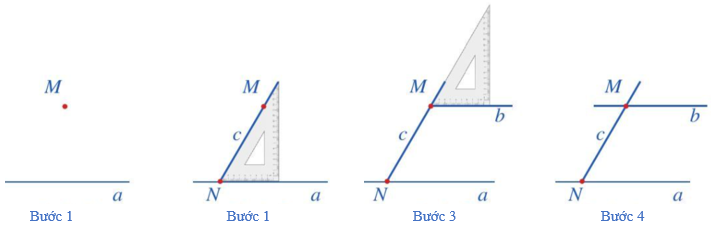 Bước 1: Vẽ đường thẳng a và điểm M không thuộc a.
Bước 1: Vẽ đường thẳng a và điểm M không thuộc a.
Bước 2: Đặt ê ke sao cho cạnh ngắn của góc vuông nằm trên đường thẳng a và cạnh huyền đi qua điểm M, vẽ theo cạnh huyền một phần đường thẳng c đi qua M (đường thẳng c cắt đường thẳng a tại điểm N).
Bước 3: Dịch chuyển ê ke sao cho cạnh huyền của ê ke vẫn nằm trên đường thẳng c còn cạnh ngắn của góc vuông đi qua điểm M, vẽ theo cạnh ngắn của góc vuông một phần đường thẳng b đi qua điểm M.
Bước 4: Vẽ hoàn thiện đường thẳng b.
Nhận xét: Qua một điểm ở ngoài một đường thẳng luôn có một đường thẳng song song với đường thẳng đó.
3. Tiên đề Euclid về đường thẳng song song
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Nhận xét: Nếu hai đường thẳng cùng đi qua điểm M và cùng song song song với đường thẳng a (M ∉ a) thì hai đường thẳng đó trùng nhau.
Ví dụ:
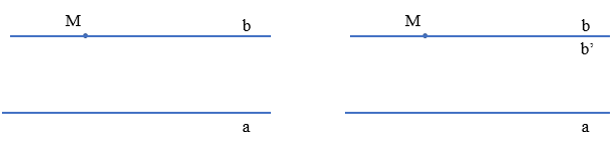 Qua điểm M nằm ngoài đường thẳng a ta vẽ được một đường thẳng b song song với a.
Qua điểm M nằm ngoài đường thẳng a ta vẽ được một đường thẳng b song song với a.
Và vẽ được đường thẳng b’ cũng đi qua M và b’ song song với a.
Khi đó theo Tiên đề Euclid thì b và b’ trùng nhau.
4. Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
- Hai góc đồng vị bằng nhau.
- Hai góc so le trong bằng nhau.
Ví dụ: Tính số đo các góc A1 và góc D2 trong hai hình vẽ sau, biết a // b và m // n.
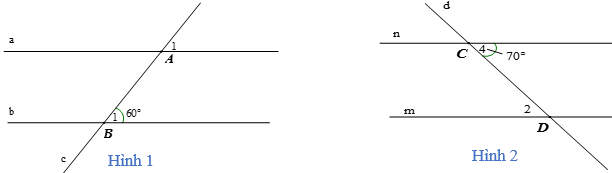
Hướng dẫn giải
- Hình 1: Do a // b nên ta có: (hai góc đồng vị), mà nên .
Vậy .
- Hình 2: Do m // n nên: (hai góc so le trong), mà nên .
Vậy .
Chú ý: Nếu đường thẳng c cắt hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau.
+ Hai góc trong cùng phía có tổng số đo bằng 180°.
Ví dụ:
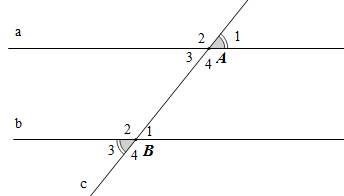
- Các cặp góc so le ngoài A1 và B3; A2 và B4; Khi đó: và .
- Hai góc trong cùng phía: góc A3 và góc B2; góc A4 và góc B1.
Khi đó: ; .
Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:
Bài 2: Tia phân giác của một góc