Với giải sách bài tập Toán 7 Bài tập cuối chương 4 sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài tập cuối chương 4

Giải Toán 7 trang 114 Tập 1

Bài 29 trang 114 Toán 7 Tập 1:

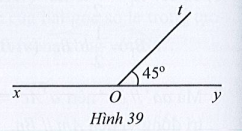
Số đo của góc xOt trong Hình 39 là:

A. 45°;

B. 135°;

C. 55°;

D. 90°.

Lời giải

Đáp án đúng là: B

Ta có $\widehat{xOt}+\widehat{tOy}=180°$ (hai góc kề bù)

Nên $\widehat{xOt}=180°-\widehat{tOy}$

Suy ra $\widehat{xOt}=180°-45°=135°.$

Vậy ta chọn phương án B.

Bài 30 trang 114 Toán 7 Tập 1:

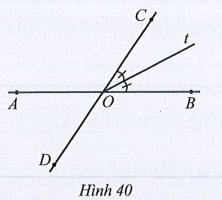
Ở Hình 40 có AB và CD cắt nhau tại O, Ot là tia phân giác của góc BOC, $\widehat{AOC}-\widehat{BOC}=68°.$ Số đo góc BOt là:

A. 56°;

B. 62°;

C. 28°;

D. 23°.

Lời giải

Đáp án đúng là: C

Ta có $\widehat{AOC}+\widehat{BOC}=180°$ (hai góc kề bù)

Mà $\widehat{AOC}-\widehat{BOC}=68°$

Suy ra $\widehat{AOC}=\frac{180°+68°}{2}=124°$ và $\widehat{BOC}=\frac{180°-68°}{2}=56°.$

Vì Ot là tia phân giác của góc BOC nên ta có:

$$\begin{gathered} \widehat{BOt}=\widehat{tOC}=\frac{1}{2}\widehat{BOC} \\ =\frac{1}{2}.56°=28°. \end{gathered}$$

Vậy ta chọn phương án C.

Bài 31 trang 114 Toán 7 Tập 1:

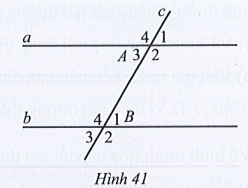
Cho Hình 41 có ${\widehat{A}}_1={\widehat{B}}_3=60°.$ Kết luận nào sau đây là sai?

A. ${\widehat{A}}_3=60°;$

B. ${\widehat{B}}_1=60°;$

C. ${\widehat{A}}_4=120°;$

D. ${\widehat{B}}_2=60°.$

Lời giải

Đáp án đúng là: D

Ta có:

• ${\widehat{A}}_3={\widehat{A}}_1=60°$ (hai góc đối đỉnh). Do đó A đúng.

• ${\widehat{B}}_3={\widehat{B}}_1=60°$(hai góc đối đỉnh). Do đó B đúng.

• ${\widehat{A}}_1+{\widehat{A}}_4=180°$ (hai góc kề bù)

Suy ra 

$$\begin{gathered} {\widehat{A}}_4=180°-{\widehat{A}}_1 \\ =180°-60°=120°. \end{gathered}$$

Do đó C đúng.

• ${\widehat{B}}_3+{\widehat{B}}_2=180°$ (hai góc kề bù)

Suy ra ${\widehat{B}}_2=180°-{\widehat{B}}_3=180°-60°=120°.$

Do đó D sai.

Vậy ta chọn phương án D.

Bài 32 trang 114 Toán 7 Tập 1:

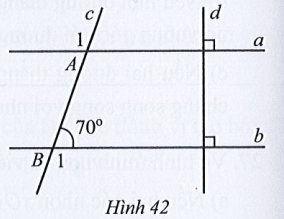
Quan sát Hình 42. Tổng số đo hai góc A₁ và B₁ là:

A. 110°;

B. 240°;

C. 180°;

D. 220°.

Lời giải

Đáp án đúng là: D

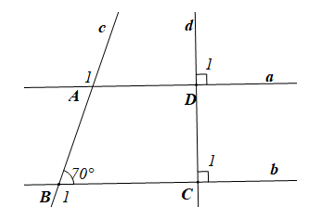
Vì $\widehat{ABC}$ và $\widehat{B_1}$ là hai góc kề bù nên ta có:

$\widehat{ABC}+{\widehat{B}}_1=180°$

Suy ra 

$$\begin{gathered} {\widehat{B}}_1=180°-\widehat{ABC} \\ =180°-70°=110°. \end{gathered}$$

Giả sử d cắt a và b lần lượt tại D và C sao cho ${\widehat{D}}_1=90°,{\widehat{C}}_1=90°$ (hình vẽ).

Do đó ${\widehat{D}}_1={\widehat{C}}_1$ (cùng bằng 90°).

Mà hai D₁ và C₁ ở vị trí đồng vị nên a //b.

Suy ra ${\widehat{A}}_1={\widehat{B}}_1$ (hai góc so le ngoài).

Do đó ${\widehat{A}}_1={\widehat{B}}_1=110°$

Nên ${\widehat{A}}_1+{\widehat{B}}_1=110°+110°=220°.$

Vậy ta chọn phương án D.

Bài 33 trang 114 Toán 7 Tập 1:

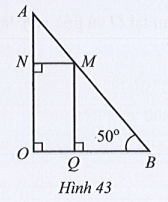
Quan sát Hình 43, biết $\widehat{MNO}=\widehat{AOB}=\widehat{BQM}=90°,$$\widehat{ABO}=50°.$ Tìm số đo mỗi góc NMQ, BMQ, MAN.

Lời giải

Ta có $\widehat{ANM}+\widehat{MNO}=180°$ (hai góc kề bù)

Suy ra 

$$\begin{gathered} \widehat{ANM}=180°-\widehat{MNO} \\ =180°-90°=90°. \end{gathered}$$

Do đó $\widehat{ANM}=\widehat{AOB}$ (cùng bằng 90°)

Mà $\widehat{ANM}$ và $\widehat{AOB}$ ở vị trí đồng vị nên MN // OB.

Suy ra:

• $\widehat{NMO}=\widehat{BQM}=90°$ (hai góc so le trong)

• $\widehat{AMN}=\widehat{ABO}=50°$ (hai góc đồng vị).

Ta có $\widehat{AMN}+\widehat{NMQ}=\widehat{AMQ}$ (hai góc kề nhau).

Mà $\widehat{AMQ}+\widehat{BMQ}=180°$ (hai góc kề bù).

Do đó $\widehat{AMN}+\widehat{NMQ}+\widehat{BMQ}=180°$

Suy ra 

$$\begin{gathered} \widehat{BMQ}=180°-\widehat{AMN}-\widehat{NMQ} \\ =180°-50°-90°=40°. \end{gathered}$$

Ta lại có: $\widehat{AOB}=\widehat{BQM}$ (cùng bằng 90°)

Mà $\widehat{AOB}$ và $\widehat{BQM}$ ở vị trí đồng vị nên MQ // AO.

Suy ra $\widehat{MAN}=\widehat{BMQ}=40°$ (hai góc đồng vị).

Vậy $\widehat{NMO}=90°,\widehat{BMQ}=40°$ và $\widehat{MAN}=40°.$

Giải Toán 7 trang 115 Tập 1

Bài 34 trang 115 Toán 7 Tập 1:

Quan sát Hình 44, biết ME vuông góc với AB tại E và ME, MF lần lượt là tia phân giác của góc AMB và AMC. Vì sao hai đường thẳng MF và AB song song với nhau?

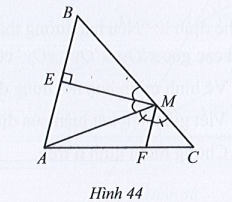
Lời giải

Vì ME, MF lần lượt là tia phân giác của góc AMB và AMC nên:

$\widehat{AME}=\widehat{BME}=\frac{1}{2}\widehat{AMB}$ và $\widehat{AMF}=\widehat{CMF}=\frac{1}{2}\widehat{AMC}$

Mặt khác $\widehat{AMB}$ và $\widehat{AMC}$ là hai góc kề bù nên ta có:

$\widehat{AMB}+\widehat{AMC}=180°$

Lại có $\widehat{AME}$ và $\widehat{AMF}$ là hai góc kề nhau nên:

$\widehat{AME}+\widehat{AMF}=\widehat{EMF}$

Do đó 

$$\begin{gathered} \widehat{EMF}=\widehat{AME}+\widehat{AMF} \\ =\frac{1}{2}\widehat{AMB}+\frac{1}{2}\widehat{AMC} \end{gathered}$$

Hay

$$\begin{gathered} \widehat{EMF}=\frac{1}{2}\left(\widehat{AMB}+\widehat{AMC}\right) \\ =\frac{1}{2}.180°=90°. \end{gathered}$$

Suy ra $\widehat{EMF}=\widehat{BEM}$ (cùng bằng 90°).

Mà $\widehat{EMF}$ và $\widehat{BEM}$ là hai góc so le trong nên MF // AB.

Vậy MF và AB song song với nhau.

Bài 35 trang 115 Toán 7 Tập 1:

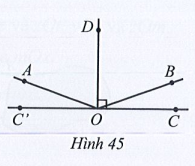
Quan sát Hình 45. Cho OD vuông góc với CC’ tại O, $\widehat{AOC}=160°,$ $\widehat{AOB}-\widehat{BOC}=120°.$

a) Tính số đo mỗi góc AOB, BOC.

b) Tia OD có là tia phân giác của góc AOB hay không?

c) So sánh hai góc AOC và BOC’.

Lời giải

a) Vì $\widehat{AOB}$ và $\widehat{BOC}$ là hai góc kề nhau nên ta có:

$\widehat{AOB}+\widehat{BOC}=\widehat{AOC}=160°$

Mà $\widehat{AOB}-\widehat{BOC}=120°.$

Nên $\widehat{AOB}=\frac{160°+120°}{2}=140°$ và $\widehat{BOC}=\frac{160°-120°}{2}=20°.$

Vậy $\widehat{AOB}=140°$ và $\widehat{BOC}=20°.$

b) Vì OD ⊥ CC’ tại O nên $\widehat{COD}=90°$

Do hai góc BOC và BOD là hai góc kề nhau nên:

$\widehat{BOC}+\widehat{BOD}=\widehat{COD}$

Suy ra 

$$\begin{gathered} \widehat{BOD}=\widehat{COD}-\widehat{BOC} \\ =90°-20°=70° \end{gathered}$$

Do hai góc AOD và COD là hai góc kề nhau nên:

$\widehat{AOD}+\widehat{COD}=\widehat{AOC}$

Suy ra 

$$\begin{gathered} \widehat{AOD}=\widehat{AOC}-\widehat{COD} \\ =160°-90°=70° \end{gathered}$$

Do đó $\widehat{BOD}=\widehat{AOD}$ (cùng bằng 70°).

Mặt khác tia OD nằm giữa hai tia OA và OB nên tia OD là tia phân giác của góc AOB.

Vậy tia OD là tia phân giác của góc AOB.

c) Ta có $\widehat{BO{C}^{\text{'}}}+\widehat{BOC}=180°$ (hai góc kề bù)

Suy ra 

$$\begin{gathered} \widehat{BO{C}^{\text{'}}}=180°-\widehat{BOC} \\ =180°-20°=160°. \end{gathered}$$

Do đó $\widehat{AOC}=\widehat{BO{C}^{\text{'}}}$ (cùng bằng 160°).

Vậy $\widehat{AOC}=\widehat{BO{C}^{\text{'}}}.$

Bài 36 trang 115 Toán 7 Tập 1:

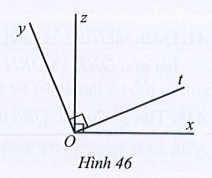
Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot.

a) Hai góc xOt và yOz có bằng nhau hay không?

b) Chứng tỏ $\widehat{xOy}+\widehat{zOt}=180°.$

c) Vẽ tia Ou là tia phân giác của góc tOz. Tia Ou có phải là tia phân giác của góc xOy hay không?

Lời giải

a) Do hai góc xOt và tOz là hai góc kề nhau nên ta có:

$\widehat{xOt}+\widehat{tOz}=\widehat{xOz}=90°$ (Ox ⊥ Oz).

Suy ra $\widehat{xOt}=90°-\widehat{tOz}$   (1)

Do hai góc yOz và tOz là hai góc kề nhau nên ta có:

$\widehat{yOz}+\widehat{tOz}=\widehat{yOt}=90°$ (Oy ⊥ Ot).

Suy ra $\widehat{yOz}=90°-\widehat{tOz}$   (2)

Từ (1) và (2) ta có $\widehat{xOt}=\widehat{yOz}.$

Vậy $\widehat{xOt}=\widehat{yOz}.$

b) Ta có hai góc xOz và yOz là hai góc kề nhau nên ta có:

$\widehat{xOz}+\widehat{yOz}=\widehat{xOy}$

Khi đó

$$\begin{gathered} \widehat{xOy}+\widehat{zOt}=\widehat{xOz}+\widehat{yOz}+\widehat{zOt} \\ =\widehat{xOz}+\left(\widehat{yOz}+\widehat{zOt}\right)=\widehat{xOz}+\widehat{yOt} \end{gathered}$$

= 90° + 90° = 180°.

Vậy $\widehat{xOy}+\widehat{zOt}=180°.$

c)

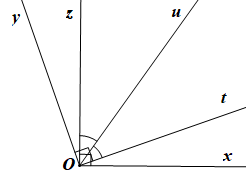
Do hai góc xOt và tOu là hai góc kề nhau nên ta có:

$\widehat{xOt}+\widehat{tOu}=\widehat{xOu}$

Do hai góc uOz và yOz là hai góc kề nhau nên ta có:

$\widehat{uOz}+\widehat{yOz}=\widehat{uOy}$

Mà Ou là tia phân giác của $\widehat{tOz}$ nên $\widehat{tOu}=\widehat{uOz}$.

$\widehat{xOt}=\widehat{zOy}$ (theo phần a).

Suy ra $\widehat{xOu}=\widehat{yOu}$

Mặt khác tia Ou nằm giữa hai tia Ox và Oy nên Ou có phải là tia phân giác của góc xOy.

Vậy Ou có phải là tia phân giác của góc xOy.

Bài 37 trang 115 Toán 7 Tập 1: Quan sát Hình 47.

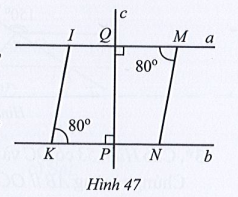
a) Vì sao hai đường thẳng a và b song song với nhau?

b) Tìm số đo góc MIK.

c) Vì sao hai đường thẳng MN và IK song song với nhau?

Lời giải

a) Ta có $\widehat{MQP}=\widehat{QPN}$ (cùng bằng 90°).

Mà hai góc MQP và QPN là hai góc ở vị trí so le trong nên a // b.

Vậy a // b.

b) Vì a // b (theo phần a) nên $\widehat{MIK}+\widehat{IKN}=180°$

Suy ra 

$$\begin{gathered} \widehat{MIK}=180°-\widehat{IKN} \\ =180°-80°=100°. \end{gathered}$$

Vậy $\widehat{MIK}=100°.$

c) Do hai góc IMN và aMN là hai góc kề bù nên ta có:

$\widehat{IMN}+\widehat{aMN}=180°$

Suy ra 

$$\begin{gathered} \widehat{aMN}=180°-\widehat{IMN} \\ =180°-80°=100°. \end{gathered}$$

Do đó $\widehat{MIK}=\widehat{aMN}$ (cùng bằng 100°).

Mà hai góc MIN và aMN ở vị trí đồng vị nên MN // IK.

Vậy MN // IK.

Bài 38* trang 115 Toán 7 Tập 1: Tìm số đo góc BCD trong Hình 48, biết AB // DE.

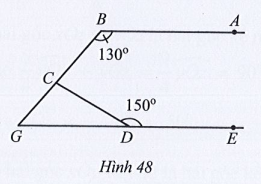
Lời giải

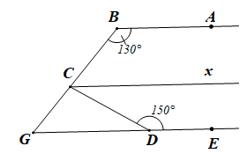
Kẻ Cx // AB (hình vẽ).

Do Cx // AB nên $\widehat{ABC}+\widehat{BCx}=180°$ (hai góc trong cùng phía).

Suy ra 

$$\begin{gathered} \widehat{BCx}=180°-\widehat{ABC} \\ =180°-130°=50°. \end{gathered}$$

Do AB // DE nên $\widehat{ABC}+\widehat{BGE}=180°$ (hai góc trong cùng phía)

Suy ra 

$$\begin{gathered} \widehat{BGE}=180°-\widehat{ABC} \\ =180°-130°=50°. \end{gathered}$$

Khi đó $\widehat{BCx}=\widehat{BGE}$ (cùng bằng 50°).

Mà hai góc BCx và BGE ở vị trí đồng vị nên Cx // GE.

Suy ra $\widehat{xCD}+\widehat{CDE}=180°$ (hai góc trong cùng phía)

Do đó 

$$\begin{gathered} \widehat{xCD}=180°-\widehat{CDE} \\ =180°-150°=30°. \end{gathered}$$

Ta có hai góc BCx và xCD là hai góc kề nhau nên:

$$\begin{gathered} \widehat{BCD}=\widehat{BCx}+\widehat{xCD} \\ =50°+30°=80°. \end{gathered}$$

Vậy $\widehat{BCD}=80°.$

Bài 39 trang 115 Toán 7 Tập 1: Quan sát Hình 49.

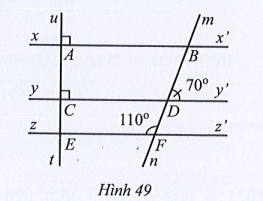
Chứng tỏ:

a) yy’ // zz’;

b) ut ⊥ zz’;

c) xx’ // zz’.

Lời giải

a) Ta có $\widehat{DFE}+\widehat{DF{z}^{\text{'}}}=180°$ (hai góc kề bù)

Suy ra  

$$\begin{gathered} \widehat{DF{z}^{\text{'}}}=180°-\widehat{DFE} \\ =180°-100°=70°. \end{gathered}$$

Do đó $\widehat{DF{z}^{\text{'}}}=\widehat{mD{y}^{\text{'}}}$ (cùng bằng 70°).

Mà $\widehat{DF{z}^{\text{'}}}$ và $\widehat{mD{y}^{\text{'}}}$ ở vị trí đồng vị nên yy’ // zz’.

Vậy yy’ // zz’.

b) Vì yy’ // zz’ (theo phần a) nên ta có:

$\widehat{uE{z}^{\text{'}}}=\widehat{uC{y}^{\text{'}}}=90°$ (hai góc đồng vị).

Do đó ut ⊥ zz’.

Vậy ut ⊥ zz’.

c) Ta có $\widehat{uAx\text{'}}=\widehat{uE{z}^{\text{'}}}$ (cùng bằng 90°).

Mà $\widehat{uAx\text{'}}$ và $\widehat{uE{z}^{\text{'}}}$ ở vị trí đồng vị nên xx’ // zz’.

Vậy xx’ // zz’.

Giải Toán 7 trang 116 Tập 1

Bài 40* trang 116 Toán 7 Tập 1: Quan sát Hình 50, trong đó vết bẩn đã xóa mất đỉnh O của góc xOy. Sử dụng định lí phát biểu trong Bài tập 26b, nêu cách vẽ đường thẳng đi qua điểm M và vuông góc với tia phân giác của góc xOy.

Lời giải

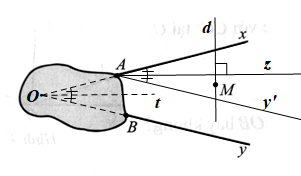
Kẻ Ay’ // By, khi đó ta có $\widehat{xA{y}^{\text{'}}}=\widehat{xOy}$ (hai góc đồng vị).

Vẽ tia Az là tia phân giác của góc xAy’.

Khi đó $\widehat{xAz}=\frac{1}{2}\widehat{xA{y}^{\text{'}}}=\frac{1}{2}\widehat{xOy}$

Vẽ tia Ot là tia phân giác của góc xOy.

Khi đó $\widehat{xOt}=\frac{1}{2}\widehat{xOy}$

Do đó $\widehat{xAz}=\widehat{xOt}$ (cùng bằng $\frac{1}{2}\widehat{xOy}$).

Mà $\widehat{xAz}$ và $\widehat{xOt}$ ở vị trí đồng vị nên Az // Ot.

Như vậy, qua điểm M kẻ đường thẳng d vuông góc với Az thì đường thẳng d là đường thẳng đi qua điểm M và vuông góc với tia phân giác của góc xOy (theo định lí phát biểu trong Bài tập 26b).

Bài 41 trang 116 Toán 7 Tập 1: Quan sát Hình 51, biết Ox // HK, tia Ox là tia phân giác của góc yOK. Chứng minh hai góc OHK và OKH bằng nhau.

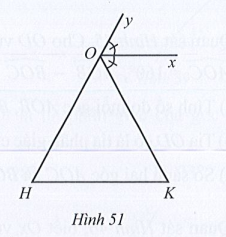
Lời giải

Vì Ox là tia phân giác của góc yOK nên $\widehat{xOy}=\widehat{xOK}$

Do Ox // HK nên ta có:

• $\widehat{xOy}=\widehat{OHK}$ (hai góc đồng vị);

• $\widehat{xOK}=\widehat{OKH}$ (hai góc so le trong).

Do đó $\widehat{OHK}=\widehat{OKH}$ (cùng bằng $\widehat{xOy}$ và $\widehat{xOK}$).

Vậy $\widehat{OHK}=\widehat{OKH}.$

Bài 42* trang 116 Toán 7 Tập 1: Tìm số đo góc QRS trong Hình 52, biết aa’ // cc’.

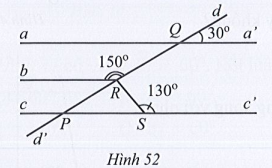
Lời giải

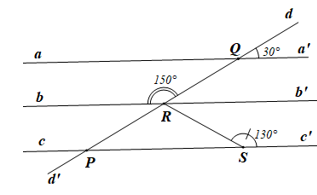
Kẻ Rb’ là tia đối của tia Rb (hình vẽ trên).

• Ta có $\widehat{QRb}+\widehat{QR{b}^{\text{'}}}=180°$ (hai góc kề bù)

Suy ra 

$$\begin{gathered} \widehat{QR{b}^{\text{'}}}=180°-\widehat{QRb} \\ =180°-150°=30°. \end{gathered}$$

• Do aa’ // cc’ nên $\widehat{dP{c}^{\text{'}}}=\widehat{dQ{a}^{\text{'}}}=30°$ (hai góc đồng vị)

Khi đó $\widehat{dP{c}^{\text{'}}}=\widehat{QR{b}^{\text{'}}}$ (cùng bằng 30°).

Mà $\widehat{dP{c}^{\text{'}}}$ và $\widehat{QR{b}^{\text{'}}}$ ở vị trí đồng vị nên bb’ // cc’.

Suy ra $\widehat{SR{b}^{\text{'}}}+\widehat{RS{c}^{\text{'}}}=180°$ (hai góc trong cùng phía).

Do đó 

$$\begin{gathered} \widehat{SR{b}^{\text{'}}}=180°-\widehat{RS{c}^{\text{'}}} \\ =180°-130°=50°. \end{gathered}$$

• Vì hai góc QRb’ và SRb’ là hai góc kề nhau nên:

$$\begin{gathered} \widehat{QRS}=\widehat{QR{b}^{\text{'}}}+\widehat{SR{b}^{\text{'}}} \\ =30°+50°=80°. \end{gathered}$$

Vậy $\widehat{QRS}°=80°.$

Bài 43* trang 116 Toán 7 Tập 1: Cho Hình 53 có OC và DE cùng vuông góc với OD, $\widehat{BAO}=120°,\widehat{AOD}=150°.$Chứng tỏ rằng AB // OC // DE.

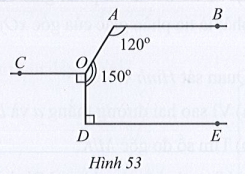
Lời giải

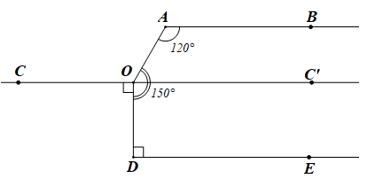
Kẻ OC’ là tia đổi của tia OC (hình vẽ trên).

• Do $\widehat{COD}=\widehat{ODE}$ (cùng bằng 90°).

Mà $\widehat{COD}$ và $\widehat{ODE}$ ở vị trí so le trong nên OC // DE.

Suy ra $\widehat{DO{C}^{\text{'}}}+\widehat{ODE}=180°$ (hai góc trong cùng phía)

Do đó 

$$\begin{gathered} \widehat{DO{C}^{\text{'}}}=180°-\widehat{ODE} \\ =180°-90°=90°. \end{gathered}$$

• Do hai góc AOC’ và DOC’ là hai góc kề nhau nên:

$\widehat{AOC’}+\widehat{DOC’}=\widehat{AOD}$

Suy ra 

$$\begin{gathered} \widehat{AOC’}=\widehat{AOD}-\widehat{DOC’} \\ =150°-90°=60°. \end{gathered}$$

• Ta có $\widehat{AOC}+\widehat{AO{C}^{\text{'}}}=180°$ (hai góc kề bù)

Suy ra 

$$\begin{gathered} \widehat{AOC}=180°-\widehat{AO{C}^{\text{'}}} \\ =180°-60°=120°. \end{gathered}$$

Do đó $\widehat{BAO}=\widehat{AOC}$ (cùng bằng 120°).

Mà $\widehat{BAO}$ và $\widehat{AOC}$ ở vị trí so le trong nên AB // OC.

Do OC // DE và AB // OC nên AB // OC // DE (hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau).

Vậy AB // OC // DE

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 4 : Định lí

Bài tập cuối chương 4

Bài 1 : Thu thập, phân loại và biểu diễn dữ liệu

Bài 2 : Phân tích và xử lí số liệu

Bài 3 : Biểu đồ đoạn thẳng

Lý thuyết Toán 7 Chương 4: Góc. Đường thẳng song song

1. Góc ở vị trí đặc biệt

1.1 Hai góc kề nhau

Hai góc kề nhau là hai góc có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.

Tính chất:

- Cho góc xOz (khác góc bẹt) và tia Oy nằm trong góc đó. Khi đó hai góc xOy và yOz là hai góc kề nhau và $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

- Nếu góc xOz là góc bẹt thì với mỗi tia Oy (khác hai tia Ox, Oz), ta cũng có: $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

1.2 Hai góc bù nhau. Hai góc kề bù

- Hai góc bù nhau là hai góc có tổng bằng 180°.

- Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù.

Chú ý: Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau là hai góc kề bù.

1.3 Hai góc đối đỉnh

- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Hai góc đối đỉnh thì bằng nhau.

2. Tia phân giác của một góc

2.1 Định nghĩa

Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

2.2 Vẽ tia phân giác của một góc

Cho góc xOy. Để vẽ tia phân giác của góc xOy ta có các cách sau:

Cách 1: Vẽ tia phân giác của một góc bằng thước thẳng và compa.

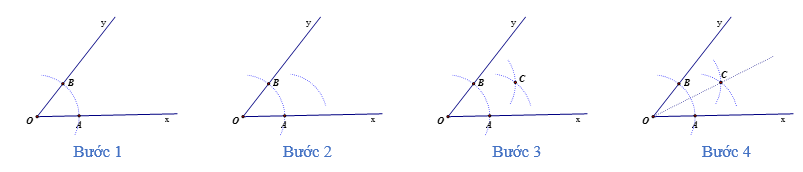
Bước 1: Trên tia Ox lấy điểm A bất kì (A khác O). Vẽ một phần đường tròn tâm O bán kính OA, cắt tia Oy tại điểm B.

Bước 2: Vẽ một phần đường tròn tâm A bán kính AO.

Bước 3: Vẽ một phần đường tròn tâm B bán kính AO, cắt phần đường tròn tâm A bán kính AO tại điểm C nằm trong góc xOy.

Bước 4: Vẽ tia OC, ta được tia phân giác của góc xOy.

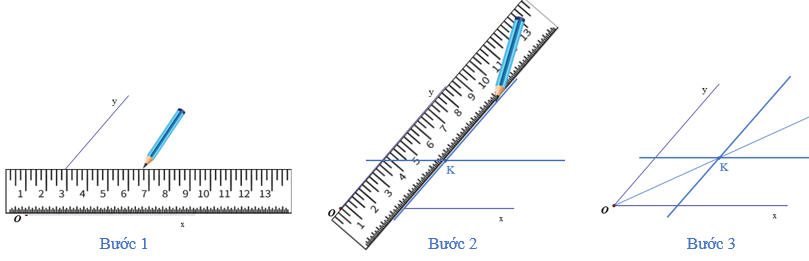
Cách 2: Dùng thước hai lề

Bước 1: Đặt thước hai lề sao cho một cạnh của thước trùng với một trong hai cạnh của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.

Bước 2: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh còn lại của góc xOy; dùng bút, vạch một vạch thẳng theo cạnh kia của thước.

Bước 3: Hai nét vạch ở bước 1 và bước 2 cắt nhau tại điểm K nằm trong góc xOy. Vẽ tia OK, ta được tia này là tia phân giác của góc xOy.

3. Hai đường thẳng song song

3.1 Hai góc đồng vị. Hai góc so le trong

Đường thẳng c cắt hai đường thẳng a, b lần lượt tại điểm A, B.

Khi đó, ta thấy:

+ Góc A₁ và góc B₁ ở “cùng một phía” của đường thẳng c.

+ Góc A₁ ở “phía trên” đường thẳng a. Góc B₁ cũng ở “phía trên” đường thẳng b.

Hai góc A₁ và B₁ ở vị trí như thế được gọi là hai góc đồng vị.

+ Góc A₃ và góc B₁ ở “hai phía” của đường thẳng c.

+ Góc A₃ ở “phía dưới” của đường thẳng a. Góc B₁ lại ở “phía trên” của đường thẳng b.

Hai góc A₃ và B₁ ở vị trí như thế gọi là hai góc so le trong.

3.2 Dấu hiệu nhận biết hai đường thẳng song song

- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a và b song song với nhau.

- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a và b song song với nhau.

Nhận xét: Qua một điểm ở ngoài một đường thẳng luôn có một đường thẳng song song với đường thẳng đó.

3.3 Tiên đề Euclid về đường thẳng song song

Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Nhận xét: Nếu hai đường thẳng cùng đi qua điểm M và cùng song song song với đường thẳng a (M ∉ a) thì hai đường thẳng đó trùng nhau.

3.4 Tính chất của hai đường thẳng song song

Nếu một đường thẳng cắt hai đường thẳng song song thì:

- Hai góc đồng vị bằng nhau.

- Hai góc so le trong bằng nhau.

Chú ý: Nếu đường thẳng c cắt hai đường thẳng song song a và b thì:

+ Hai góc so le ngoài bằng nhau.

+ Hai góc trong cùng phía có tổng số đo bằng 180⁰.

4. Định lý

4.1 Định lí

Khẳng định có các tính chất sau thì được gọi là định lý:

- Là một phát biểu về một tính chất toán học;

- Tính chất toán học đó đã được chứng tỏ là đúng không dựa vào trực giác hay đo đạc,..

Nhận xét:

+ Định lý thường được phát biểu dưới dạng “Nếu … thì …”.

+ Phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết, phần nằm sau từ “thì” là phần kết luận.

4.2 Chứng minh định lý

Chứng minh định lý là một tiến trình lập luận từ giả thiết suy ra kết luận là đúng.