Với giải sách bài tập Toán 10 Bài 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm

Giải SBT Toán 10 trang 37 Tập 2

Bài 14 trang 37 SBT Toán 10 Tập 2: Cho mẫu số liệu:     21     22     23     24     25

a) Khoảng biến thiên của mẫu số liệu trên là:

A. 1.

B. 2.

C. 3.

D. 4.

b) Khoảng tứ phân vị của mẫu số liệu trên là:

A. 1.

B. 2.

C. 3.

D. 4.

c) Phương sai của mẫu số liệu trên là:

A. 1.

B. 2.

C. 3.

D. 4.

d) Độ lệch chuẩn của mẫu số liệu trên là:

A. 1.

B. $\sqrt{2}$ .

C. $\sqrt{3}$ .

D. 4.

Lời giải:

a) Trong mẫu số liệu trên, số lớn nhất là 25 và số nhỏ nhất là 21.

Vậy khoảng biến thiên của mẫu số liệu trên là: R = x_max – x_min = 25 – 21 = 4.

Do đó ta chọn phương án D.

b) Mẫu số liệu trên đã được sắp xếp theo thứ tự không giảm.

Trung vị của mẫu số liệu trên là: M_e = 23.

Trung vị của dãy 21; 22 là: $\frac{21+22}{2}=\mathrm{21,5}$ .

Trung vị của dãy 24; 25 là: $\frac{24+25}{2}=\mathrm{24,5}$ .

Suy ra Q₁ = 21,5; Q₂ = 23; Q₃ = 24,5.

Do đó khoảng tứ phân vị của mẫu số liệu trên là: ∆_Q = Q₃ – Q₁ = 24,5 – 21,5 = 3.

Vậy ta chọn phương án C.

c) Số trung bình cộng của mẫu số liệu trên là: $\overline{x}=\frac{21+22+23+24+25}{5}=23$ .

Ta có (21 – 23)² + (22 – 23)² + (23 – 23)² + (24 – 23)² + (25 – 23)² = 10.

Phương sai của mẫu số liệu trên là: $s^2=\frac{10}{5}=2$ .

Vậy ta chọn phương án B.

d) Độ lệch chuẩn của mẫu số liệu trên là: $s=\sqrt{s^2}=\sqrt{2}$ .

Vậy ta chọn phương án B.

Giải SBT Toán 10 trang 38 Tập 2

Bài 15 trang 38 SBT Toán 10 Tập 2: Biểu đồ đoạn thẳng ở Hình 2 biểu diễn thu nhập bình quân đầu người/năm của Việt Nam ở một số năm trong giai đoạn từ 1986 đến 2020.

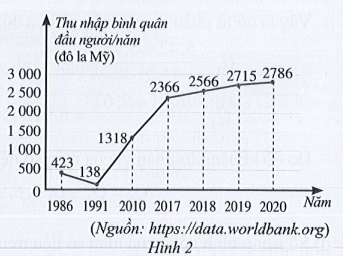
Mẫu số liệu nhận được từ biểu đồ ở Hình 2 có khoảng biến thiên là bao nhiêu?

A. 71.

B. 85.

C. 1 180.

D. 2 648.

Lời giải:

Mẫu số liệu thống kê thu nhập bình quân đầu người/năm nhận được từ biểu đồ trên là:

423     138     1318     2366     2566     2715     2786

Trong mẫu số liệu trên, số lớn nhất là 2786 và số nhỏ nhất là 138.

Vậy khoảng biến thiên của mẫu số liệu trên là: R = x_max – x_min = 2786 – 138 = 2648.

Do đó ta chọn phương án D.

Bài 16 trang 38 SBT Toán 10 Tập 2: Biểu đồ đoạn thẳng ở Hình 3 biểu diễn số lượt khách vào một cửa hàng trong ngày đầu khai trương tại một số mốc thời gian.

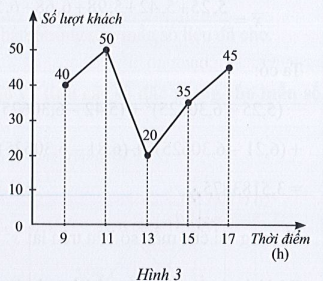
Mẫu số liệu nhận được từ biểu đồ ở Hình 3 có khoảng tứ phân vị là bao nhiêu?

A. 10.

B. 15.

C. 20.

D. 5.

Lời giải:

Mẫu số liệu thống kê số lượt khách vào một cửa hàng trong ngày đầu khai trương nhận được từ biểu đồ trên là:

40     50     20     35     45

Sắp xếp mẫu số liệu trên theo thứ tự không giảm, ta được dãy:

20     35     40     45     50

Trung vị của mẫu số liệu trên là: M_e = 40.

Trung vị của dãy 20; 35 là: $\frac{20+35}{2}=\mathrm{27,5}$ .

Trung vị của dãy 45; 50 là: $\frac{45+50}{2}=\mathrm{47,5}$ .

Vậy Q₁ = 27,5; Q₂ = 40; Q₃ = 47,5.

Suy ra khoảng tứ phân vị của mẫu số liệu trên là: ∆_Q = Q₃ – Q₁ = 47,5 – 27,5 = 20.

Do đó ta chọn phương án C.

Bài 17 trang 38 SBT Toán 10 Tập 2: Cho mẫu số liệu:     1     11     13     15     17       21

a) Tìm khoảng biến thiên của mẫu số liệu trên.

b) Tìm khoảng tứ phân vị của mẫu số liệu trên.

c) Tính phương sai và độ lệch chuẩn của mẫu số liệu trên.

d) Tìm giá trị bất thường của mẫu số liệu trên.

Lời giải:

a) Trong mẫu số liệu trên, số lớn nhất là 21 và số nhỏ nhất là 1.

Vậy khoảng biến thiên của mẫu số liệu trên là: R = x_max – x_min = 21 – 1 = 20.

b) Mẫu số liệu trên đã được sắp xếp theo thứ tự không giảm.

Trung vị của mẫu số liệu trên là: $\frac{13+15}{2}=14$ .

Trung vị của dãy 1; 11; 13 là: 11.

Trung vị của dãy 15; 17; 21 là 17.

Vậy Q₁ = 11; Q₂ = 14; Q₃ = 17.

Do đó khoảng tứ phân vị của mẫu số liệu trên là: ∆_Q = Q₃ – Q₁ = 17 – 11 = 6.

c) Số trung bình cộng của mẫu số liệu trên là: $\overline{x}=\frac{1+11+13+15+17+21}{6}=13$ .

Ta có (1 – 13)² + (11 – 13)² + (13 – 13)² + (15 – 13)² + (17 – 13)² + (21 – 13)² = 232.

Phương sai của mẫu số liệu trên là: $s^2=\frac{232}{6}=\frac{116}{3}$ .

Độ lệch chuẩn của mẫu số liệu trên là: $s=\sqrt{s^2}=\sqrt{\frac{116}{3}}=\frac{2\sqrt{87}}{3}$ .

d) Ta có:

⦁ $Q_1-\frac{3}{2}{\Delta }_Q=11-\frac{3}{2}.6=2$ ;

⦁ $Q_3+\frac{3}{2}{\Delta }_Q=17+\frac{3}{2}.6=26$ .

Ta thấy 1 < 2.

Vậy 1 là giá trị bất thường của mẫu số liệu đã cho.

Bài 18 trang 38 SBT Toán 10 Tập 2: Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:

(Nguồn: https://nchmf.gov.vn)

a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên.

b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải:

a) Mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên là:

23     25     26     27     27     27     27     21     19     18

b) Số trung bình cộng của mẫu số liệu trên là:

$\overline{x}=\frac{23+25+26+27+27+27+27+21+19+18}{10}=24$ (°C)

Ta có (23 – 24)² + (25 – 24)² + (26 – 24)² + (27 – 24)² + (27 – 24)² + (27 – 24)²

+ (27 – 24)² + (21 – 24)² + (19 – 24)² + (18 – 24)² = 112.

Phương sai của mẫu số liệu trên là: $s^2=\frac{112}{10}=\mathrm{11,2}$ .

Độ lệch chuẩn của mẫu số liệu trên là: $s=\sqrt{s^2}=\sqrt{\mathrm{11,2}}=\frac{2\sqrt{70}}{5}$  (°C).

Bài 19 trang 38 SBT Toán 10 Tập 2: Biểu đồ đoạn thẳng ở Hình 4 cho biết kết quả thi Ngoại ngữ ở câu lạc bộ của Dũng (đường nét liền) và Hoàng (đường nét đứt đậm) qua 9 lần kiểm tra.

a) Viết mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng và Hoàng nhận được từ biểu đồ ở Hình 4.

b) Tìm khoảng biến thiên và khoảng tứ phân vị của mỗi mẫu số liệu đó.

c) Tính phương sai và độ lệch chuẩn của hai mẫu số liệu đó. Cho biết kết quả thi của bạn nào ổn định hơn?

Lời giải:

a) Mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng là:

8     9     7     9     7     8     8     7     9     (1)

Mẫu số liệu thống kê kết quả thi ngoại ngữ của Hoàng là:

6     10     8     8     7     9     6     9     8     (2)

b) Xét mẫu số liệu (1):

⦁ Trong mẫu số liệu (1), số điểm lớn nhất là 9 và số điểm thấp nhất là 7.

Do đó khoảng biến thiên của mẫu số liệu (1) là: R = x_max – x_min = 9 – 7 = 2.

⦁ Sắp xếp mẫu số liệu (1) theo thứ tự không giảm, ta được dãy:

7     7     7     8     8     8     9     9     9

Trung vị của mẫu số liệu trên là: 8.

Trung vị của dãy 7; 7; 7; 8 là: $\frac{7+7}{2}=7$ .

Trung vị của dãy 8; 9; 9; 9 là: $\frac{9+9}{2}=9$ .

Vì vậy Q₁ = 7; Q₂ = 8; Q₃ = 9.

Do đó khoảng tứ phân vị của mẫu số liệu (1) là: ∆_Q = Q₃ – Q₁ = 9 – 7 = 2.

Xét mẫu số liệu (2):

⦁ Trong mẫu số liệu (2), số điểm lớn nhất là 10 và số điểm thấp nhất là 6.

Do đó khoảng biến thiên của mẫu số liệu (1) là: R = x_max – x_min = 10 – 6 = 4.

⦁ Sắp xếp mẫu số liệu (2) theo thứ tự không giảm, ta được dãy:

6     6     7     8     8     8     9     9     10

Trung vị của mẫu số liệu trên là: 8.

Trung vị của dãy 6; 6; 7; 8 là: $\frac{6+7}{2}=\mathrm{6,5}$ .

Trung vị của dãy 8; 9; 9; 10 là: $\frac{9+9}{2}=9$ .

Vì vậy Q₁ = 6,5; Q₂ = 8; Q₃ = 9.

Do đó khoảng tứ phân vị của mẫu số liệu (2) là: ∆_Q = Q₃ – Q₁ = 9 – 6,5 = 2,5.

Vậy ta có:

⦁ Khoảng biến thiên của mẫu số liệu (1) và (2) lần lượt là 2 và 4.

⦁ Khoảng tứ phân vị của mẫu số liệu (1) và (2) lần lượt là 2 và 2,5.

c) Gọi kết quả trung bình của bạn Dũng và bạn Hoàng lần lượt là ${\overline{x}}_D,{\overline{x}}_H$ . Ta có:

⦁ ${\overline{x}}_D=\frac{7.3+8.3+9.3}{9}=8$  (điểm).

⦁ ${\overline{x}}_H=\frac{6.2+7+8.3+9.2+10}{9}=\frac{71}{9}$  (điểm).

Gọi phương sai tương ứng với mẫu số liệu (1) và (2) lần lượt là $s_D^2,s_H^2$ . Ta có:

⦁ $s_D^2=\frac{3.{\left(7-8\right)}^2+3.{\left(8-8\right)}^2+3.{\left(9-8\right)}^2}{9}=\frac{2}{3}$ .

⦁ $s_H^2=\frac{2.{\left(6-\frac{71}{9}\right)}^2+{\left(7-\frac{71}{9}\right)}^2+3.{\left(8-\frac{71}{9}\right)}^2+2.{\left(9-\frac{71}{9}\right)}^2+{\left(10-\frac{71}{9}\right)}^2}{9}=\frac{134}{81}$ .

Độ lệch chuẩn của mẫu số liệu (1) là: $s_D=\sqrt{s_D^2}=\sqrt{\frac{2}{3}}=\frac{\sqrt{6}}{3}$ .

Độ lệch chuẩn của mẫu số liệu (2) là: $s_H=\sqrt{s_H^2}=\sqrt{\frac{134}{81}}=\frac{\sqrt{134}}{9}$ .

Do $s_D^2=\frac{2}{3}<s_H^2=\frac{134}{81}$ .

Nên bạn Dũng có kết quả thi ổn định hơn bạn Hoàng.

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

SBT Toán 10 Bài 2: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm

SBT Toán 10 Bài 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm

SBT Toán 10 Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản

SBT Toán 10 Bài 1: Tọa độ của vectơ

SBT Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ

Lý thuyết Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm

I. Khoảng biến thiên. Khoảng tứ phân vị

1. Định nghĩa

- Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.

Ta có thể tính khoảng biến thiên R của mẫu số liệu theo công thức sau: R = x_max – x_min, trong đó x_max là giá trị lớn nhất, x_min là giá trị nhỏ nhất của mẫu số liệu đó.

- Giả sử Q₁, Q₂, Q₃ là tứ phân vị của mẫu số liệu. Ta gọi hiệu ∆_Q = Q₃ – Q₁ là khoảng tứ phân vị của mẫu số liệu đó.

Chú ý: Khoảng tứ phân vị của mẫu số liệu còn gọi là khoảng trải giữa (tiếng Anh là InterQuartile Range – IQR) của mẫu số liệu đó.

Ví dụ: Mẫu số liệu thống kê cân nặng (đơn vị: kg) của 8 học sinh trong một tổ như sau:

45      52      41      37      50      52      66      49

a) Tìm khoảng biến thiên của mẫu số liệu trên.

b) Tìm khoảng tứ phân vị của mẫu số liệu trên.

Hướng dẫn giải

a) Trong mẫu có số liệu lớn nhất là 66, số liệu nhỏ nhất là 37.

Khi đó, khoảng biến thiên của mẫu là R = x_max­ – x_min = 66 – 37 = 29 (kg).

Vậy khoảng biến thiên của mẫu là R = 29 kg.

b) Sắp xếp mẫu theo thứ tự tăng dần, ta được:

37      41      45      49      50      52      52      66

Khi đó, trung vị của mẫu là: Q₂ = $\frac{49+50}{2}=49,5$.

Q₁ là trung vị của mẫu 37, 41, 45, 49 nên Q₁ = $\frac{41+45}{2}=43$.

Q₃ là trung vị của mẫu 50, 52, 52, 66 nên Q₃ = $\frac{52+52}{2}=52$.

Khi đó, ta có khoảng tứ phân vị là:

∆_Q = Q₃ – Q₁ = 52 – 43 = 9 (kg).

Vậy khoảng tứ phân vị của mẫu là ∆_Q = 9 kg.

2. Ý nghĩa

a) Ý nghĩa của khoảng biến thiên: Khoảng biến thiên của mẫu số liệu phản ánh sự “dao động”, “sự dàn trải” của các số liệu trong mẫu đó. Khoảng biến thiên được sử dụng trong nhiều tình huống thực tiễn, chẳng hạn: tìm ra sự phân tán điểm kiểm tra của một lớp học hay xác định phạm vi giá cả của một dịch vụ …

Theo cách nhìn như ở trong vật lí, ở đó biên độ dao động phản ánh khoảng cách từ điểm cân bằng đến điểm xa nhất của dao động, nếu coi số trung bình cộng là “điểm cân bằng” của mẫu số liệu thì khoảng biến thiên của mẫu số liệu có thể xem như hai lần biên độ dao động của các số liệu trong mẫu đó quanh điểm cân bằng.

Trong các đại lượng đo mức độ phân tán của mẫu số liệu, khoảng biến thiên là đại lượng dễ hiểu, dễ tính toán và tương đối tốt đối với các mẫu số liệu nhỏ. Tuy nhiên, do khoảng biến thiên chỉ sử dụng hai giá trị x_max và x_min của mẫu số liệu nên đại lượng đó chưa diễn giải đầy đủ sự phân tán của số liệu trong mẫu. Ngoài ra, giá trị của khoảng biến thiên sẽ bị ảnh hưởng bởi các giá trị bất thường của mẫu số liệu đó. Trong những trường hợp như vậy, khoảng biến thiên của mẫu số liệu không phản ánh chính xác độ dàn trải của mẫu số liệu.

b) Ý nghĩa của khoảng tứ phân vị: Khoảng tứ phân vị là đại lượng cho biết mức độ phân tán của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp và có thể giúp xác định các giá trị bất thường của mẫu số liệu đó. Khoảng tứ phân vị thường được sử dụng thay cho khoảng biến thiên vì nó loại trừ hầu hết giá trị bất thường của mấu số liệu.

II. Phương sai

1. Định nghĩa

- Mỗi hiệu số giữa số liệu và số trung bình cộng gọi là độ lệch của số liệu đó đối với số trung bình cộng.

- Cho mẫu số liệu thống kê có n giá trị x₁, x₂, …, x_n và số trung bình cộng là $\overline{x}$.

Ta gọi số  $s^2=\frac{{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+{\left(x_n-\overline{x}\right)}^2}{n}$ là phương sai của mẫu số liệu trên.

Nhận xét:

- Khi có các số liệu bằng nhau, ta có thể tính phương sai theo công thức sau:

+ Đối với bảng tần số:

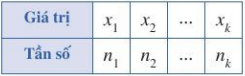
Phương sai của mẫu số liệu thống kê trong bảng phân bố tần số là:

$s^2=\frac{n_1{\left(x_1-\overline{x}\right)}^2+n_2{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+n_k{\left(x_k-\overline{x}\right)}^2}{n},$

trong đó n = n₁ + n₂ + …+ n_k ; $\overline{x}$ là số trung bình cộng của các số liệu đã cho.

+ Đối với bảng phân bố tần số tương đối:

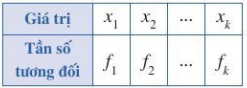
Phương sai của mẫu số liệu thống kê trong bảng phân bố tần số tương đối là:

$s^2=f_1{\left(x_1-\overline{x}\right)}^2+f_2{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+f_k{\left(x_k-\overline{x}\right)}^2,$

trong đó $\overline{x}$ là số trung bình cộng của số liệu đã cho. 

- Trong thực tế, người ta còn dùng công thức sau để tính phương sai của mẫu số liệu:

${\widehat{s}}^2=\frac{{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+{\left(x_n-\overline{x}\right)}^2}{n-1},$

trong đó: x_i là giá trị của quan sát thứ i; $\overline{x}$ là giá trị trung bình và n là số quan sát trong mẫu số liệu đó.

Ví dụ: Hai lớp 10A và 10B của một trường THPT đồng thời làm bài thi môn Toán theo cùng một đề thi. Kết quả được ghi lại trong bảng tần số sau:

Điểm thi của lớp 10A:

Điểm thi của lớp 10B:

a) Tính phương sai của từng mẫu số liệu ở hai bảng trên.

b) Xét xem kết quả bài thi của lớp nào đồng đều hơn.

Hướng dẫn giải

Ta có điểm thi trung bình của lớp 10A là:

${\overline{x}}_{10A}=\frac{3.5+7.6+12.7+14.8+3.9+1.10}{3+7+12+14+3+1}=7,25$

Điểm thi trung bình của lớp 10A là:

${\overline{x}}_{10B}=\frac{8.6+18.7+10.8+4.9}{8+18+10+4}=7,25$

Ta có phương sai của mẫu số liệu lớp 10A là:

$s_{10A}^2=\frac{3{\left(5-7,25\right)}^2+7{\left(6-7,25\right)}^2+\mathrm{...}+1.{\left(10-7,25\right)}^2}{3+7+12+14+3+1}=1,2875$

⇒ $s_{10A}^2$ = 1,2875

Ta có phương sai của mẫu số liệu lớp 10B là:

$s_{10B}^2=\frac{8{\left(6-7,25\right)}^2+18{\left(7-7,25\right)}^2+10.{\left(8-7,25\right)}^2+4.{\left(9-7,25\right)}^2}{8+18+10+4}=0,7875$

⇒ $s_{10B}^2$ = 0,7875.

Ta thấy điểm thi trung bình của lớp 10A và 10B bằng nhau đều bằng 7,25. Nhưng phương sai bảng điểm của lớp 10A lại lớn hơn phương sai bảng điểm lớp 10B nên kết quả làm bài thi của lớp 10B đồng đều hơn lớp 10A.

2. Ý nghĩa

Phương sai là số đặc trưng đo mức độ phân tán của mẫu số liệu. Mẫu số liệu nào có phương sai nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn.

III. Độ lệch chuẩn

1. Định nghĩa 

Căn bậc hai (số học) của phương sai gọi là độ lệch chuẩn của mẫu số liệu thống kê.

Nhận xét: Vì độ lệch chuẩn có cùng đơn vị đo với số liệu thống kê nên khi cần chú ý đến đơn vị đo thì ta sử dụng độ lệch chuẩn mà không sử dụng phương sai.

Ví dụ: Cho mẫu số liệu:

23      22      20      12      35

Tính độ lệch chuẩn của mẫu trên.

Hướng dẫn giải

Mẫu trên có 5 số liệu.

Số trung bình của mẫu trên là: $\overline{x}=\frac{23+22+20+12+35}{5}=22,4$.

Phương sai của mẫu số liệu đó là:

$s^2=\frac{{\left(23-22,4\right)}^2+{\left(22-22,4\right)}^2+{\left(20-22,4\right)}^2+{\left(12-22,4\right)}^2+{(35-22,4)}^2}{5}=54,64$

⇒ s = $\sqrt{s^2}$ = $\sqrt{54,64}$ ≈ 7,39.

Vậy độ lệch chuẩn của mẫu là 7,39.

2. Ý nghĩa

Cũng như phương sai, khi hai mấu số liệu thống kê có cùng đơn vị đo và có số trung bình cộng bằng nhau (hoặc xấp xỉ nhau), mẫu số liệu nào có độ lệch chuẩn nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn. Độ lệch chuẩn là số đặc trưng đo mức độ phân tán của mẫu số liệu thống kê có cùng đơn vị đo.

IV. Tính hợp lí của số liệu thống kê

Ta có thể sử dụng các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm để chỉ ra được những số liệu bất thường của mẫu số liệu đó. Ta thường sử dụng khoảng tứ phân vị để xác định số liệu bất thường của mẫu số liệu. Cụ thể như sau:

Giả sử Q₁, Q₂, Q₃ là tứ phân vị của mẫu số liệu và hiệu ∆_Q = Q₃ – Q₁ là khoảng tứ phân vị của mẫu số liệu đó. Một giá trị trong mẫu số liệu được coi là một giá trị bất thường nếu nó nhỏ hơn $Q_1-\frac{3}{2}{\Delta }_Q$ hoặc lớn hơn $Q_3+\frac{3}{2}{\Delta }_Q$. Như vậy, khoảng tứ phân vị cho ta cách nhận biết giá trị bất thường của mẫu số liệu.

Chú ý: Ta cũng có thể xác định số liệu bất thường của mẫu số liệu bằng số trung bình cộng và độ lệch chuẩn. Cụ thể như sau:

Giả sử $\overline{x}$, s lần lượt là số trung bình cộng và độ lệch chuẩn của mẫu số liệu. Một giá trị trong mẫu số liệu cũng được coi là một giá trị bất thường nếu nó nhỏ hơn $\overline{x}$ – 3s hoặc lớn hơn $\overline{x}$ + 3s. Như vậy, số trung bình cộng và độ lệch chuẩn cho ta cách nhận ra giá trị bất thường của mẫu số liệu.

Ví dụ: Hãy tìm các giá trị bất thường của mẫu số liệu sau:

12      4        10      –5      6        7        9        30

Hướng dẫn giải

Mẫu được sắp xếp theo thứ tự tăng dần là:

–5      4        6        7        9        10      12      30

Mẫu có 8 số liệu

Trung vị của mẫu là: $\frac{7+9}{2}$ = 8. Suy ra Q₂ = 8.

Trung vị nửa dưới –5, 4, 6, 7 là $\frac{4+6}{2}$ = 5. Suy ra Q₁ = 5.

Trung vị nửa trên 9, 10, 12, 30 là $\frac{10+12}{2}$ = 11. Suy ra Q₃ = 11.

Khoảng tứ phân vị là ∆_Q = Q₃ – Q₁ = 11 – 5 = 6.

Ta có: $Q_1-\frac{3}{2}{\Delta }_Q=5-\frac{3}{2}.6=-4$; $Q_3+\frac{3}{2}{\Delta }_Q=11+\frac{3}{2}.6=20$.

Ta thấy –5 < –4 và 30 > 20 nên các giá trị –5 và 30 là các giá trị bất thường của mẫu.

Vậy mẫu có hai giá trị bất thường là –5 và 30.