Với giải sách bài tập Toán 10 Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Giải SBT Toán 10 trang 122 Tập 1

Bài 1 trang 122 SBT Toán 10 Tập 1: Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

a) 15; 15; 12; 14; 17; 16; 16; 15; 15.

b) 5; 7; 4; 3; 5; 6; 7; 8; 9; 7; 2.

c) 7; 6; 8; 7; 7; 4; 5; 10; 9; 9; 8; 5.

d) 87; 87; 88; 88; 70; 83; 85; 86; 97; 89; 92; 89; 90.

Lời giải:

a) Ta có: n = 9

Sắp xếp mẫu số liệu theo thứ tự không giảm:

12; 14; 15; 15; 15; 15; 16; 16; 17

+) Số trung bình:

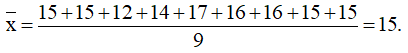
+) Vì n = 9 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 15.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 12; 14; 15; 15.

Vậy Q₁ = (14 + 15) : 2 = 14,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 15; 16; 16; 17.

Vậy Q₃ = (16 + 16) : 2 = 16.

+) Vì số 15 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (4 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 15.

b) Ta có: n = 11

Sắp xếp mẫu số liệu theo thứ tự không giảm:

2; 3; 4; 5; 5; 6; 7; 7; 7; 8; 9

+) Số trung bình:

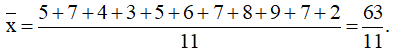
+) Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 6.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 2; 3; 4; 5; 5.

Vậy Q₁ = 4.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 7; 7; 7; 8; 9.

Vậy Q₃ = 7.

+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (3 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 7.

c) Ta có: n = 12

Sắp xếp mẫu số liệu theo thứ tự không giảm:

4; 5; 5; 6; 7; 7; 7; 8; 8; 9; 9; 10

+) Số trung bình:

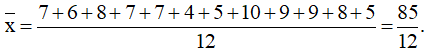
+) Vì n = 12 là số chẵn nên ta có tứ phân vị thứ hai Q₂ = (7 + 7) : 2 = 7.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 4; 5; 5; 6; 7; 7.

Vậy Q₁ = (5 + 6) : 2 = 5,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 7; 8; 8; 9; 9; 10.

Vậy Q₃ = (8 + 9) : 2 = 8,5.

+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (3 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 7.

d) Ta có: n = 13

Sắp xếp mẫu số liệu theo thứ tự không giảm:

70; 83; 85; 86; 87; 87; 88; 88; 89; 89; 90; 92; 97

+) Số trung bình:

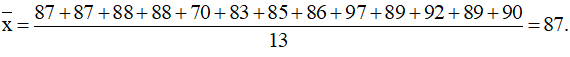
+) Vì n = 13 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 88.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 70; 83; 85; 86; 87; 87.

Vậy Q₁ = (85 + 86) : 2 = 85,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 88; 89; 89; 90; 92; 97.

Vậy Q₃ = (89 + 90) : 2 = 89,5.

+) Vì số 87, 88, 89 là các giá trị xuất hiện nhiều nhất trong mẫu số liệu (2 lần). Nên suy ra Mốt của mẫu số liệu là M_o ∈ {87; 88; 89}.

Bài 2 trang 122 SBT Toán 10 Tập 1: Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

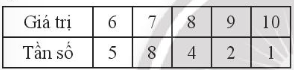
a)

b)

Lời giải:

a)

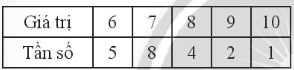
Ta có: n = 5 + 8 + 4 + 2 + 1 = 20

Sắp xếp mẫu số liệu theo thứ tự không giảm:

6; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 8; 9; 9; 10

+) Số trung bình:

$\overline{x}=\frac{6.5+7.8+8.4+9.2+10.1}{20}=7,3.$

+) Vì n = 20 là số chẵn nên ta có tứ phân vị thứ hai Q₂ = (7 + 7) : 2 = 7.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 6; 6; 6; 6; 6; 7; 7; 7; 7; 7.

Vậy Q₁ = (6 + 7) : 2 = 6,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 7; 7; 7; 8; 8; 8; 8; 9; 9; 10.

Vậy Q₃ = (8 + 8) : 2 = 8.

+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (8 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 7.

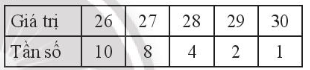
b)

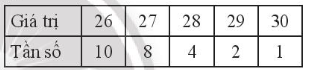
Ta có: n = 10 + 8 + 4 + 2 + 1 = 25

Sắp xếp mẫu số liệu theo thứ tự không giảm:

26; 26; 26; 26; 26; 26; 26; 26; 26; 26; 27; 27; 27; 27; 27; 27; 27; 27; 28; 28; 28; 28; 29; 29; 30

+) Số trung bình:

$$\begin{gathered} \overline{x}=\frac{26.10+27.8+28.4+29.2+30.1}{25} \\ =27,04. \end{gathered}$$

+) Vì n = 25 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 27.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 26; 26; 26; 26; 26; 26; 26; 26; 26; 26; 27; 27.

Vậy Q₁ = (26 + 26) : 2 = 26.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 27; 27; 27; 27; 27; 28; 28; 28; 28; 29; 29; 30.

Vậy Q₃ = (28 + 28) : 2 = 28.

+) Vì số 26 là các giá trị xuất hiện nhiều nhất trong mẫu số liệu (10 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 26.

Bài 3 trang 122 SBT Toán 10 Tập 1: Tổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ năm 2010 đến 2020 được thể hiện trong biểu đồ sau (đơn vị: mm).

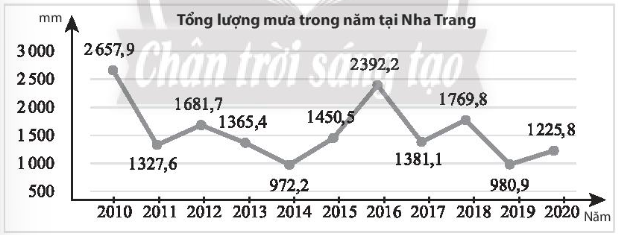
a) Hãy tính lượng mưa trung bình tại trạm quan trắc trên từ năm 2010 đến 2020.

b) Hãy tìm các tứ phân vị của mẫu số liệu đó.

Lời giải:

a) Từ năm 2010 đến 2020 có tất cả 11 năm

Lượng mưa trung bình tại trạm quan trắc trên từ năm 2010 đến 2020 là:

b) Sắp xếp lượng mưa các năm theo thứ tự không giảm là:

972,2; 980,9; 1225,8; 1327,6; 1365,4; 1381,1; 1450,5; 1681,7; 1769,8; 2392,2; 2657,9

Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 1381,1.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 972,2; 980,9; 1225,8; 1327,6; 1365,4.

Vậy Q₁ = 1225,8.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 1450,5; 1681,7; 1769,8; 2392,2; 2657,9.

Vậy Q₃ = 1769,8.

Bài 4 trang 122, 123 SBT Toán 10 Tập 1: Số huy chương vàng và bạc trong các giải thể thao quốc tế mà đoàn thể thao Việt Nam đạt được tại các giải đấu ở châu Á trong các năm từ năm 2010 đến 2019 được thống kê ở bảng sau:

(Nguồn: Tổng cục Thống kê)

a) Tìm số trung bình và trung vị huy chương vàng và huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên.

b) Hãy so sánh số huy chương vàng đoàn thể thao Việt Nam đạt được trong giai đoạn 2010 – 2014 với giai đoạn 2015 – 2019.

Lời giải:

a) Từ năm 2010 đến 2019 có tất cả 10 năm.

+) Trung bình số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong 10 năm trên là:

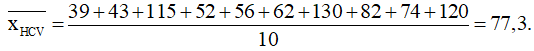
+) Trung bình số huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên là:

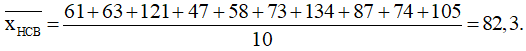
+) Sắp xếp mẫu số liệu số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong 10 năm trên theo thứ tự không giảm là:

39; 43; 52; 56; 62; 74; 82; 115; 120; 130.

Vì n = 10 là số chẵn nên trung vị số huy chương vàng đạt được trong 10 năm là: (62 + 74) : 2 = 68.

+) Sắp xếp mẫu số liệu số huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên theo thứ tự không giảm là:

47; 58; 61; 63; 73; 74; 87; 105; 121; 134.

Vì n = 10 là số chẵn nên trung vị số huy chương bạc đạt được trong 10 năm là: (73 + 74) : 2 = 73,5.

b) * Từ năm 2010 – 2014 có 5 năm

+) Trung bình số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong giai đoạn 2010 – 2014 là:

$\overline{x_1}=\frac{39+43+115+52+56}{5}=61.$

+) Sắp xếp mẫu số liệu số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong giai đoạn 2010 – 2014 theo thứ tự không giảm là:

39; 43; 52; 56; 115.

Vì n₁ = 5 là số lẻ nên trung vị số huy chương vàng đạt được trong giai đoạn 2010 – 2014 là: 52.

* Từ năm 2015 – 2019 có 5 năm

+) $\overline{x_2}=\frac{62+130+82+74+120}{5}=93,6.$

+) Sắp xếp mẫu số liệu số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong giai đoạn 2015 – 2019 theo thứ tự không giảm là:

62; 74; 82; 120; 130.

Vì n₂ = 5 là số lẻ nên trung vị số huy chương vàng đạt được trong giai đoạn 2015 – 2019 là: 82.

Vậy nếu so sánh theo số trung bình và số trung vị thì Việt Nam đều giành được nhiều huy chương vàng hơn trong giai đoạn 2015 – 2019 so với giai đoạn 2010 – 2014.

Giải SBT Toán 10 trang 123 Tập 1

Bài 5 trang 123 SBT Toán 10 Tập 1: Bảng sau ghi lại độ tuổi của hai nhóm vận động viên tham gia một cuộc thi.

a) Hãy so sánh độ tuổi của hai nhóm vận động viên theo số trung bình và trung vị.

b) Tìm tứ phân vị của độ tuổi vận động viên cả hai nhóm gộp lại.

Lời giải:

a)

+) Nhóm 1 có tất cả 12 vận động viên

Sắp xếp mẫu số liệu theo thứ tự không giảm:

17; 20; 22; 27; 29; 29; 30; 31; 31; 32; 32; 32

Số trung bình:

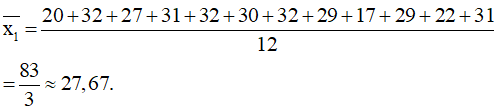
Vì n = 12 là số chẵn nên số trung vị của mẫu số liệu ở nhóm 1 là:

M_e1 = (29 + 30) : 2 = 29,5.

+) Nhóm 2 có tất cả 12 vận động viên

Sắp xếp mẫu số liệu theo thứ tự không giảm:

20; 21; 22; 22; 29; 29; 29; 29; 30; 31; 31; 32

Số trung bình:

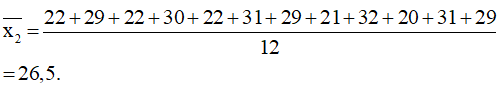
Vì n = 12 là số chẵn nên số trung vị của mẫu số liệu ở nhóm 2 là:

M_e2 = (29 + 29) : 2 = 29

Vậy nếu so sánh theo số trung bình và số trung vị thì độ tuổi của các vận động viên nhóm 1 cao hơn nhóm 2.

b) Cả hai nhóm gộp lại có tất cả 24 vận động viên

Sắp xếp độ tuổi của các vận động viên theo thứ tự không giảm ta có mẫu số liệu:

17; 20; 20; 21; 22; 22; 22; 27; 29; 29; 29; 29; 29; 29; 30; 30; 31; 31; 31; 31; 32; 32; 32; 32

Vì n = 24 là số chẵn nên ta có tứ phân vị thứ hai Q₂ = (29 + 29) : 2 = 29.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 17; 20; 20; 21; 22; 22; 22; 27; 29; 29; 29; 29.

Vậy Q₁ = (22 + 22) : 2 = 22.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 29; 29; 30; 30; 31; 31; 31; 31; 32; 32; 32; 32.

Vậy Q₃ = (31 + 31) : 2 = 31.

Bài 6 trang 123 SBT Toán 10 Tập 1: Minh và Thủy ghi lại số thư điện tử mà mỗi người nhận được mỗi ngày trong 10 ngày được lựa chọn ngẫu nhiên từ tháng 01/2021 ở bảng sau:

a) Hãy tìm số trung bình, trung vị và mốt của số thư điện tử mà mỗi bạn nhận được theo số liệu trên.

b) Nếu so sánh theo số trung bình thì ai nhận được nhiều thư điện tử hơn?

c) Nếu so sánh theo trung vị thì ai nhận được nhiều thư điện tử hơn?

d) Nên dùng số trung bình hay số trung vị để so sánh xem ai nhận được nhiều thư điện tử hơn mỗi ngày?

Lời giải:

a)

+) Sắp xếp số thư điện tử mà Minh nhận được trong 10 ngày theo thứ tự không giảm: 1; 1; 1; 3; 4; 4; 5; 6; 6; 7

Số trung bình của số thư điện tử mà bạn Minh nhận được:

$$\begin{gathered} \overline{x_1}=\frac{6+7+3+6+1+4+1+4+5+1}{10} \\ =3,8. \end{gathered}$$

Vì n = 10 là số lẻ nên trung vị số thư điện tử mà Minh nhận được trong 10 ngày là: M_e1 = (4 + 4) : 2 = 4.

Vì giá trị 1 xuất hiện nhiều nhất (3 lần) nên suy ra mốt của mẫu số liệu trên là M_o1 = 1.

+) Sắp xếp số thư điện tử mà Thủy nhận được trong 10 ngày theo thứ tự không giảm: 1; 1; 2; 2; 2; 2; 3; 3; 4; 20

Số trung bình của số thư điện tử mà bạn Thủy nhận được:

$$\begin{gathered} \overline{x_2}=\frac{2+3+1+2+3+4+1+2+20+2}{10} \\ =4. \end{gathered}$$

Vì n = 10 là số lẻ nên trung vị số thư điện tử mà Thủy nhận được trong 10 ngày là: M_e2 = (2 + 2) : 2 = 2.

Vì giá trị 2 xuất hiện nhiều nhất (4 lần) nên suy ra mốt của mẫu số liệu trên là M_o2 = 2.

b) Nếu so sánh theo số trung bình thì Thủy nhận được nhiều thư điện tử hơn Minh (4 > 3,8).

c) Nếu so sánh theo số trung vị thì Minh nhận được nhiều thư điện tử hơn Thủy (4 > 2)

d) Nên dùng số trung vị để so sánh xem ai nhận được nhiều thư điện tử hơn mỗi ngày vì trong bảng thống kê ta thấy dãy số liệu của bạn Thủy có một số liệu quá lớn so với các số liệu còn lại (là số 20). 

Bài 7 trang 123, 124 SBT Toán 10 Tập 1: Bạn Út ghi lại khối lượng của một số quả xoài Keo và xoài Thanh Ca ở bảng sau (đơn vị: gam).

a) Sử dụng số trung bình, hãy so sánh khối lượng của hai loại xoài.

b) Sử dụng trung vị, hãy so sánh khối lượng của hai loại xoài.

c) Hãy tính các tứ phân vị của hai mẫu số liệu trên.

d) Nếu bạn Út mua 5 kg xoài Keo thì sẽ được khoảng bao nhiêu quả?

Nếu bạn Út mua 5 kg xoài Thanh Ca thì sẽ được khoảng bao nhiêu quả?

Lời giải:

a) +) Xoài Keo có tất cả 11 quả được chọn để ghi khối lượng.

Khối lượng trung bình của khối lượng Xoài Keo là:                  

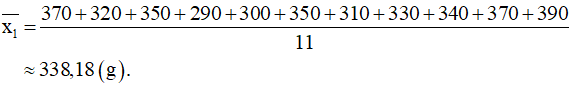
+) Xoài Thanh Ca có tất cả 12 quả được chọn để ghi khối lượng.

Khối lượng trung bình của khối lượng Xoài Thanh Ca là:          

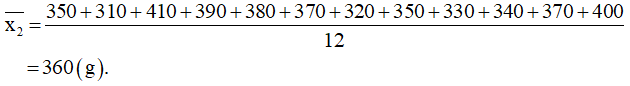
Vậy nếu so sánh theo số trung bình thì khối lượng xoài Thanh Ca cao hơn khối lượng xoài Keo.

b) +) Sắp xếp khối lượng mỗi quả Xoài Keo theo thứ tự không giảm:

290; 300; 310; 320; 330; 340; 350; 350; 370; 370; 390

Vì n = 11 là số lẻ nên số trung vị của khối lượng xoài Keo là:

M_e1 = 340 (g).

+) Sắp xếp khối lượng mỗi quả Xoài Thanh Ca theo thứ tự không giảm:

310; 320; 330; 340; 350; 350; 370; 370; 380; 390; 400; 410

Vì n = 12 là số chẵn số trung vị của khối lượng xoài Thanh Ca là:

M_e2 = (350 + 370) : 2 = 360 (g).

Vậy nếu so sánh theo số trung vị thì khối lượng xoài Thanh Ca cao hơn khối lượng xoài Keo.

c) +) Sắp xếp khối lượng mỗi quả Xoài Keo theo thứ tự không giảm:

290; 300; 310; 320; 330; 340; 350; 350; 370; 370; 390

Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 340.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 290; 300; 310; 320; 330.

Vậy Q₁ = 310.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 350; 350; 370; 370; 390.

Vậy Q₃ = 370.

+) Sắp xếp khối lượng mỗi quả Xoài Thanh Ca theo thứ tự không giảm:

310; 320; 330; 340; 350; 350; 370; 370; 380; 390; 400; 410

Vì n = 12 là số chẵn nên ta có tứ phân vị thứ hai

Q₂ = (350 + 370) : 2 = 360.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 310; 320; 330; 340; 350; 350.

Vậy Q₁ = (330 + 340) : 2 = 335.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 370; 370; 380; 390; 400; 410.

Vậy Q₃ = (380 + 390) : 2 = 385.

d) Do 5 000 : 338,18 ≈ 14,79 nên nếu bạn Út mua 5 kg xoài Keo thì sẽ mua được khoảng 14 đến 15 quả.

Do 5 000 : 360 ≈ 13,89 nên nếu bạn Út mua 5 kg xoài Thanh Ca thì sẽ mua được khoảng 13 đến 14 quả.

Giải SBT Toán 10 trang 124 Tập 1

Bài 8 trang 124 SBT Toán 10 Tập 1: Số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Đồng bằng sông Hồng và khu vực Trung du và miền núi phía Bắc vào năm 2019 được cho như sau:

Đồng bằng sông Hồng: 30; 7; 7; 10; 10; 15; 9; 7; 5; 9; 6.

Trung du và miền núi phía Bắc: 10; 12; 7; 6; 8; 8; 7; 10; 9; 12; 9; 7; 11; 10.

(Nguồn: Tổng cục Thống kê)

a) Mỗi khu vực nêu trên có bao nhiêu tỉnh/thành phố?

b) Sử dụng số trung bình, hãy so sánh số đơn vị hành chính cấp quận/huyện/thị xã của các tỉnh/thành phố ở hai khu vực.

c) Sử dụng trung vị, hãy so sánh số đơn vị hành chính cấp quận/huyện/thị xã của các tỉnh/thành phố ở hai khu vực.

d) Hãy giải thích tại sao lại có sự khác biệt khi so sánh bằng số trung bình và trung vị.

e) Hãy tìm tứ phân vị và mốt của hai khu vực.

Lời giải:

a) Khu vực Đồng bằng Sông Hồng có 11 tỉnh/thành phố (do có 11 số liệu trong dãy số liệu). Khu vực Trung du và miền núi phía Bắc có 14 tỉnh/thành phố (do có 14 số liệu trong dãy số liệu).

b)

+) Trung bình số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Đồng bằng sông Hồng vào năm 2019 là:

$$\begin{gathered} \overline{x_1} \\ =\frac{30+7+7+10+10+15+9+7+5+9+6}{11} \\ \approx 10,45. \end{gathered}$$

+) Trung bình số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Trung du và miền núi phía Bắc vào năm 2019 là:

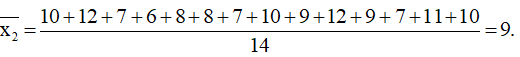
Vậy theo số trung bình thì các các tỉnh/ thành phố khu vực Đồng bằng sông Hồng có nhiều đơn vị hành chính cấp quận/ huyện/ thị xã hơn khu vực Trung du và miền núi phía Bắc.

c)

+) Sắp xếp số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Đồng bằng sông Hồng vào năm 2019 theo thứ tự không giảm:

5; 6; 7; 7; 7; 9; 9; 10; 10; 15; 30

Vì n = 11 là số lẻ nên số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Đồng bằng sông Hồng vào năm 2019 là:

M_e1 = 9.

+) Sắp xếp số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Trung du và miền núi phía Bắc vào năm 2019 theo thứ tự không giảm:

6; 7; 7; 7; 8; 8; 9; 9; 10; 10; 10; 11; 12; 12

Vì n = 14 là số chẵn nên số trung vị của số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Trung du và miền núi phía Bắc vào năm 2019 là:

M_e2 = (9 + 9) : 2 = 9.

Vậy nếu so sánh theo số trung vị thì số đơn vị hành chính cấp quận/ huyện/ thị xã của các tỉnh/ thành phố khu vực Đồng bằng sông Hồng và Trung du và miền núi phía Bắc là bằng nhau.

d) Có sự khác biệt khi so sánh bằng số trung bình và số trung vị là do có một tỉnh/ thành phố khu vực ĐBSH có quá nhiều đơn vị hành chính cấp quận/ huyện/ thị xã so với các tỉnh/ thành phố khác.

e)

+) Đồng bằng Sông Hồng:

Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 9.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 5; 6; 7; 7; 7.

Vậy Q₁ = 7.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 9; 10; 10; 15; 30.

Vậy Q₃ = 10.

Vì giá trị 7 xuất hiện nhiều nhất (3 lần) nên suy ra mốt của mẫu số liệu trên là M_o = 7.

+) Trung du và miền núi phía Bắc:

Vì n = 14 là số chẵn nên ta có tứ phân vị thứ hai

Q₂ = (9 + 9) : 2 = 9.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 6; 7; 7; 7; 8; 8; 9.

Vậy Q₁ = 7.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 9; 10; 10; 10; 11; 12; 12.

Vậy Q₃ = 10.

Vì giá trị 7 và 10 xuất hiện nhiều nhất (3 lần) nên suy ra mốt của mẫu số liệu trên là M_o ∈ {7; 10}.

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài tập cuối chương 6

Bài 1: Dấu của tam thức bậc hai