Với lời giải SBT Toán 10 trang 122 Tập 1 chi tiết trong Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Bài 1 trang 122 SBT Toán 10 Tập 1: Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

a) 15; 15; 12; 14; 17; 16; 16; 15; 15.

b) 5; 7; 4; 3; 5; 6; 7; 8; 9; 7; 2.

c) 7; 6; 8; 7; 7; 4; 5; 10; 9; 9; 8; 5.

d) 87; 87; 88; 88; 70; 83; 85; 86; 97; 89; 92; 89; 90.

Lời giải:

a) Ta có: n = 9

Sắp xếp mẫu số liệu theo thứ tự không giảm:

12; 14; 15; 15; 15; 15; 16; 16; 17

+) Số trung bình:

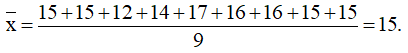
+) Vì n = 9 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 15.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 12; 14; 15; 15.

Vậy Q₁ = (14 + 15) : 2 = 14,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 15; 16; 16; 17.

Vậy Q₃ = (16 + 16) : 2 = 16.

+) Vì số 15 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (4 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 15.

b) Ta có: n = 11

Sắp xếp mẫu số liệu theo thứ tự không giảm:

2; 3; 4; 5; 5; 6; 7; 7; 7; 8; 9

+) Số trung bình:

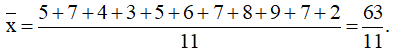
+) Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 6.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 2; 3; 4; 5; 5.

Vậy Q₁ = 4.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 7; 7; 7; 8; 9.

Vậy Q₃ = 7.

+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (3 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 7.

c) Ta có: n = 12

Sắp xếp mẫu số liệu theo thứ tự không giảm:

4; 5; 5; 6; 7; 7; 7; 8; 8; 9; 9; 10

+) Số trung bình:

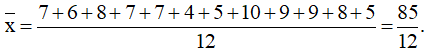
+) Vì n = 12 là số chẵn nên ta có tứ phân vị thứ hai Q₂ = (7 + 7) : 2 = 7.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 4; 5; 5; 6; 7; 7.

Vậy Q₁ = (5 + 6) : 2 = 5,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 7; 8; 8; 9; 9; 10.

Vậy Q₃ = (8 + 9) : 2 = 8,5.

+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (3 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 7.

d) Ta có: n = 13

Sắp xếp mẫu số liệu theo thứ tự không giảm:

70; 83; 85; 86; 87; 87; 88; 88; 89; 89; 90; 92; 97

+) Số trung bình:

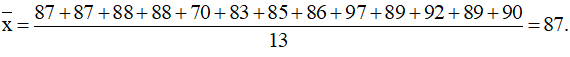
+) Vì n = 13 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 88.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 70; 83; 85; 86; 87; 87.

Vậy Q₁ = (85 + 86) : 2 = 85,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 88; 89; 89; 90; 92; 97.

Vậy Q₃ = (89 + 90) : 2 = 89,5.

+) Vì số 87, 88, 89 là các giá trị xuất hiện nhiều nhất trong mẫu số liệu (2 lần). Nên suy ra Mốt của mẫu số liệu là M_o ∈ {87; 88; 89}.

Bài 2 trang 122 SBT Toán 10 Tập 1: Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

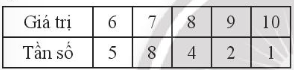
a)

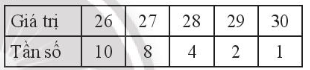
b)

Lời giải:

a)

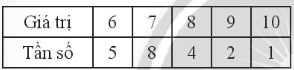
Ta có: n = 5 + 8 + 4 + 2 + 1 = 20

Sắp xếp mẫu số liệu theo thứ tự không giảm:

6; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 8; 9; 9; 10

+) Số trung bình:

$\overline{x}=\frac{6.5+7.8+8.4+9.2+10.1}{20}=7,3.$

+) Vì n = 20 là số chẵn nên ta có tứ phân vị thứ hai Q₂ = (7 + 7) : 2 = 7.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 6; 6; 6; 6; 6; 7; 7; 7; 7; 7.

Vậy Q₁ = (6 + 7) : 2 = 6,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 7; 7; 7; 8; 8; 8; 8; 9; 9; 10.

Vậy Q₃ = (8 + 8) : 2 = 8.

+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (8 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 7.

b)

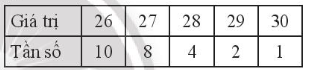
Ta có: n = 10 + 8 + 4 + 2 + 1 = 25

Sắp xếp mẫu số liệu theo thứ tự không giảm:

26; 26; 26; 26; 26; 26; 26; 26; 26; 26; 27; 27; 27; 27; 27; 27; 27; 27; 28; 28; 28; 28; 29; 29; 30

+) Số trung bình:

$$\begin{gathered} \overline{x}=\frac{26.10+27.8+28.4+29.2+30.1}{25} \\ =27,04. \end{gathered}$$

+) Vì n = 25 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 27.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 26; 26; 26; 26; 26; 26; 26; 26; 26; 26; 27; 27.

Vậy Q₁ = (26 + 26) : 2 = 26.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 27; 27; 27; 27; 27; 28; 28; 28; 28; 29; 29; 30.

Vậy Q₃ = (28 + 28) : 2 = 28.

+) Vì số 26 là các giá trị xuất hiện nhiều nhất trong mẫu số liệu (10 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 26.

Bài 3 trang 122 SBT Toán 10 Tập 1: Tổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ năm 2010 đến 2020 được thể hiện trong biểu đồ sau (đơn vị: mm).

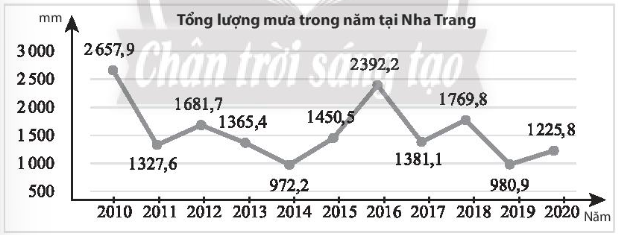
a) Hãy tính lượng mưa trung bình tại trạm quan trắc trên từ năm 2010 đến 2020.

b) Hãy tìm các tứ phân vị của mẫu số liệu đó.

Lời giải:

a) Từ năm 2010 đến 2020 có tất cả 11 năm

Lượng mưa trung bình tại trạm quan trắc trên từ năm 2010 đến 2020 là:

b) Sắp xếp lượng mưa các năm theo thứ tự không giảm là:

972,2; 980,9; 1225,8; 1327,6; 1365,4; 1381,1; 1450,5; 1681,7; 1769,8; 2392,2; 2657,9

Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 1381,1.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 972,2; 980,9; 1225,8; 1327,6; 1365,4.

Vậy Q₁ = 1225,8.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 1450,5; 1681,7; 1769,8; 2392,2; 2657,9.

Vậy Q₃ = 1769,8.

Bài 4 trang 122, 123 SBT Toán 10 Tập 1: Số huy chương vàng và bạc trong các giải thể thao quốc tế mà đoàn thể thao Việt Nam đạt được tại các giải đấu ở châu Á trong các năm từ năm 2010 đến 2019 được thống kê ở bảng sau:

(Nguồn: Tổng cục Thống kê)

a) Tìm số trung bình và trung vị huy chương vàng và huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên.

b) Hãy so sánh số huy chương vàng đoàn thể thao Việt Nam đạt được trong giai đoạn 2010 – 2014 với giai đoạn 2015 – 2019.

Lời giải:

a) Từ năm 2010 đến 2019 có tất cả 10 năm.

+) Trung bình số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong 10 năm trên là:

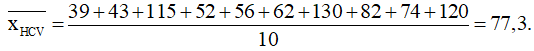
+) Trung bình số huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên là:

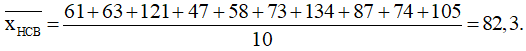
+) Sắp xếp mẫu số liệu số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong 10 năm trên theo thứ tự không giảm là:

39; 43; 52; 56; 62; 74; 82; 115; 120; 130.

Vì n = 10 là số chẵn nên trung vị số huy chương vàng đạt được trong 10 năm là: (62 + 74) : 2 = 68.

+) Sắp xếp mẫu số liệu số huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên theo thứ tự không giảm là:

47; 58; 61; 63; 73; 74; 87; 105; 121; 134.

Vì n = 10 là số chẵn nên trung vị số huy chương bạc đạt được trong 10 năm là: (73 + 74) : 2 = 73,5.

b) * Từ năm 2010 – 2014 có 5 năm

+) Trung bình số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong giai đoạn 2010 – 2014 là:

$\overline{x_1}=\frac{39+43+115+52+56}{5}=61.$

+) Sắp xếp mẫu số liệu số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong giai đoạn 2010 – 2014 theo thứ tự không giảm là:

39; 43; 52; 56; 115.

Vì n₁ = 5 là số lẻ nên trung vị số huy chương vàng đạt được trong giai đoạn 2010 – 2014 là: 52.

* Từ năm 2015 – 2019 có 5 năm

+) $\overline{x_2}=\frac{62+130+82+74+120}{5}=93,6.$

+) Sắp xếp mẫu số liệu số huy chương vàng mà đoàn thể thao Việt Nam đạt được trong giai đoạn 2015 – 2019 theo thứ tự không giảm là:

62; 74; 82; 120; 130.

Vì n₂ = 5 là số lẻ nên trung vị số huy chương vàng đạt được trong giai đoạn 2015 – 2019 là: 82.

Vậy nếu so sánh theo số trung bình và số trung vị thì Việt Nam đều giành được nhiều huy chương vàng hơn trong giai đoạn 2015 – 2019 so với giai đoạn 2010 – 2014.

Xem thêm các bài giải sách bài tập Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 123 Tập 1

Giải SBT Toán 10 trang 124 Tập 1

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài tập cuối chương 6

Bài 1: Dấu của tam thức bậc hai