Giải SBT Toán 10 trang 58 Tập 1 Chân trời sáng tạo

Nguyễn Mạnh Tài Ngày: 22-11-2022 Lớp 10

363

Với lời giải SBT Toán 10 trang 58 Tập 1 chi tiết trong Bài tập cuối chương 3 sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 3

Bài 1 trang 58 SBT Toán 10 Tập 1: Ta có bảng giá trị của hàm cầu đối với sản phẩm A theo đơn giá của sản phẩm A như sau:

Đơn giá sản phẩm A (đơn vị: nghìn đồng)	10	20	40	70	90
Lượng cầu (nhu cầu về số sản phẩm)	338	288	200	98	50

a) Giả sử hàm cầu là một hàm số bậc hai theo đơn giá x, hãy viết công thức của hàm này, biết rằng c = 392.

b) Chứng tỏ rằng hàm số này có thể viết thành dạng y = f(x) = a(b – x)².

c) Giả sử hàm cầu này lấy mọi giá trị trên đoạn [0; 100], hãy tính lượng cầu khi đơn giá sản phẩm A là 30, 50, 100.

d) Cùng giả thiết với câu c, nếu lượng cầu là 150 sản phẩm thì đơn giá sản phẩm A là khoảng bao nhiêu (đơn vị: nghìn đồng)?

Lời giải:

a) Theo giả thiết, hàm cầu là một hàm số bậc hai nên công thức của hàm số có dạng: y = f(x) = ax² + bx + 392 (a ≠ 0).

Ta chọn 2 cặp giá trị từ bảng đã cho lần lượt có x = 10, x = 20 thì được hệ phương trình sau: $\{\begin{cases} a {.10}^{2} + b .10 + 392 = 338 \\ a {.20}^{2} + b .20 + 392 = 288 \end{cases}$ .

Giải hệ phương trình trên ta được a = $\frac{1}{50}$ , b = $- \frac{28}{5}$ .

Vậy y = f(x) = $\frac{1}{50} x^{2} - \frac{28}{5} x + 392$ .

b) Ta có: $\frac{1}{50} x^{2} - \frac{28}{5} x + 392$ $= \frac{1}{50} (x^{2} - 280 x + 19600)$ $= \frac{1}{50} (x^{2} - 2.140 + 140^{2})$

$= \frac{1}{50} {(x - 140)}^{2} = \frac{1}{50} {(140 - x)}^{2}$ .

Vậy hàm số có trên có thể viết thành dạng y = f(x) = $\frac{1}{50} {(140 - x)}^{2}$ .

c) Khi x = 30 thì lượng cầu là y = f(30) = $\frac{1}{50} {(140 - 30)}^{2} = 242$ .

Khi x = 50 thì lượng cầu là y = f(50) = $\frac{1}{50} {(140 - 50)}^{2} = 162$ .

Khi x = 100 thì lượng cầu là y = f(100) = $\frac{1}{50} {(140 - 100)}^{2} = 32$ .

d) Nếu lượng cầu là 150 sản phẩm thì đơn giá sản phẩm A được tính nhờ phương trình sau: $\frac{1}{50} {(140 - x)}^{2}$ = 150

Giải phương trình trên ta có:

$\frac{1}{50} {(140 - x)}^{2}$ = 150 ⇔ (140 – x)² = 7500

$\Leftrightarrow [\begin{array}{l} 140 - x = 50 \sqrt{3} \\ 140 - x = - 50 \sqrt{3} \end{array} \Leftrightarrow [\begin{array}{l} x \approx 53, 4 \\ x \approx 226, 6 \end{array}$

Thep giả thiết câu c), hàm số xác định trên đoạn [0; 100] nên ta chọn x ≈ 53,4.

Vậy nếu lượng cầu là 150 sản phẩm thì đơn giá sản phẩm A khoảng 53 400 đồng.

Bài 2 trang 58 SBT Toán 10 Tập 1: Khi một vật từ vị trí y₀ được ném xiên lên cao theo góc α (so với phương ngang) với vận tốc ban đầu v₀ thì phương trình chuyển động của vật này là:

$y = \frac{- g x^{2}}{2 v_{0}^{2} c o s^{2} α} + \tan α . x + y_{0}$ .

a) Vật bị ném xiên như vậy có chuyển động theo đường xiên hay không? Tại sao?

b) Giả sử góc ném có số đo là 45°, vận tốc ban đầu của vật là 3 m/s và vật được ném xiên từ độ cao 1 m so với mặt đất, hãy viết phương trình chuyển động của vật.

c) Một vận động viên ném lao đã lập kỉ lục với độ xa 90 m. Biết người này ném lao từ độ cao 0,9 m và góc ném là khoảng 45°. Hỏi vận tốc đầu của lao khi được ném đi là bao nhiêu?

(Lưu ý: Lấy giá trị g = 10 m/s² cho gia tốc trọng trường và làm tròn kết quả đến 2 chữ số thập phân).

Lời giải:

a) Với các giá trị đã biết là góc ném, vận tốc ban đầu và gia tốc trọng trường g là hằng số thì phương trình chuyển động trong ném xiên là một hàm số bậc hai theo x. Do vậy đồ thị của hàm số là một parabol. Quỹ đạo chuyển động của các vật cũng là một phần trên parabol này nên nó không thể chuyển động theo đường xiên.

b) Với góc ném có số đo là 45°, vận tốc ban đầu của vật là 3 m/s và vật được ném xiên từ độ cao 1 m so với mặt đất, ta có phương trình chuyển động của vật này là:

$y = \frac{- g x^{2}}{2 v_{0}^{2} c o s^{2} α} + \tan α . x + y_{0}$ $= \frac{- 10 x^{2}}{2 . 3^{2} . c o s^{2} 45 °} + \tan 45 ° . x + 1$ $= - \frac{10}{9} x^{2} + x + 1$ .

Vậy phương trình chuyển động cần tìm là y $= - \frac{10}{9} x^{2} + x + 1$ .

c) Theo giả thiết bài toán, ta có phương trình chuyển động của lao sau khi ném là:

$y = \frac{- g x^{2}}{2 v_{0}^{2} c o s^{2} α} + \tan α . x + y_{0}$ $= \frac{- 10 x^{2}}{2 . v_{0}^{2} . c o s^{2} 45 °} + \tan 45 ° . x + 0, 9$ $= - \frac{10}{v_{0}^{2}} x^{2} + x + 0, 9$ .

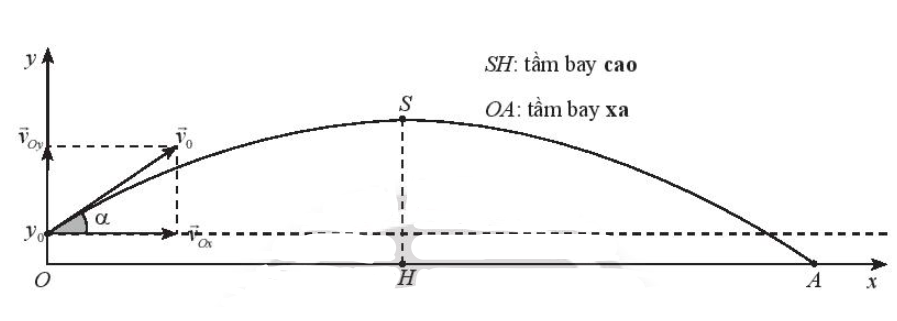
Sách bài tập Toán 10 Bài tập cuối chương 3 - Chân trời sáng tạo (ảnh 1)

Mặt khác, lao được ném đi đạt độ xa 90 m, tức là OA = 90. Nói các khác điểm A(90; 0) thuộc đồ thị hàm số nên ta có: f(90) = 0 hay $- \frac{10}{v_{0}^{2}} {.90}^{2} + 90 + 0, 9 = 0$ $\Leftrightarrow v_{0}^{2} = \frac{90000}{101}$ .