Với giải sách bài tập Toán 7 Bài 4: Phép nhân và phép chia đa thức một biến sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 4: Phép nhân và phép chia đa thức một biến

Giải Toán 7 trang 32 Tập 2

Bài 1 trang 32 Toán 7 Tập 2:Thực hiện phép nhân (7x – 2)(–2x + 5).

Lời giải:

Ta thực hiện phép nhân đa thức:

(7x – 2)(–2x + 5)

= 7x . (–2x + 5) – 2 . (–2x + 5)

= 7x . (–2x) + 7x . 5 – 2 . (–2x) – 2 . 5

= –14x² + 35x + 4x – 10

= –14x² + (35x + 4x) – 10

= –14x² + 39x – 10.

Vậy (7x – 2)(–2x + 5) = –14x² + 39x – 10.

Bài 2 trang 32 Toán 7 Tập 2:Thực hiện phép nhân (3x – 4)(–2x² + 7x + 4).

Lời giải:

Ta thực hiện phép nhân đa thức:

(3x – 4).(–2x² + 7x + 4)

= 3x . (–2x² + 7x + 4) – 4 . (–2x² + 7x + 4)

= 3x . (–2x²) + 3x . 7x + 3x . 4 – 4 . (–2x²) – 4 . 7x – 4 . 4

= –6x³ + 21x² + 12x + 8x² – 28x – 16

= –6x³ + (21x² + 8x²) + (12x – 28x) – 16

= –6x³ + 29x² – 16x – 16.

Vậy (3x – 4)(–2x² + 7x + 4) = –6x³ + 29x² – 16x – 16.

Bài 3 trang 32 Toán 7 Tập 2:Thực hiện phép nhân (4x² – 2x + 1)(–2x² + 5x + 3).

Lời giải:

Ta thực hiện phép nhân đa thức:

(4x² – 2x + 1)(–2x² + 5x + 3)

= 4x² . (–2x² + 5x + 3) – 2x . (–2x² + 5x + 3) + 1 . (–2x² + 5x + 3)

= 4x² . (–2x²) + 4x² . 5x + 4x² . 3 – 2x . (–2x²) – 2x . 5x – 2x . 3 – 2x² + 5x + 3

= –8x⁴ + 20x³ + 12x² + 4x³ – 10x² – 6x – 2x² + 5x + 3

= –8x⁴ + (20x³ + 4x³) + (12x² – 10x² – 2x²) + (– 6x + 5x) + 3

= –8x⁴ + 24x³ – x + 3.

Vậy (4x² – 2x + 1)(–2x² + 5x + 3) = –8x⁴ + 24x³ – x + 3.

Giải Toán 7 trang 33 Tập 2

Bài 4 trang 33 Toán 7 Tập 2:Hãy lập biểu thức có dạng đa thức theo biến x biểu thị diện tích của phần được tô đậm trong Hình 1.

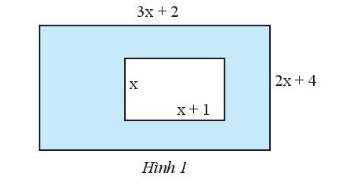
Lời giải:

Diện tích hình chữ nhật lớn có chiều dài 3x + 2 và chiều rộng 2x + 4 là:

(2x + 4)(3x + 2)

= 2x . (3x + 2) + 4 . (3x + 2)

= 6x² + 4x + 12x + 8

= 6x² + 16x + 8 (đơn vị diện tích).

Diện tích hình chữ nhật nhỏ có chiều dài x + 1 và chiều rộng x là:

x(x +1) = x² + x (đơn vị diện tích).

Diện tích của phần được tô đậm trong Hình 1 là:

6x² + 16x + 8 – (x² + x)

= 6x² + 16x + 8 – x² – x

= (6x² – x²) + (16x – x) + 8

= 5x² + 15x + 8 (đơn vị diện tích).

Vậy biểu thức có dạng đa thức theo biến x biểu thị diện tích của phần được tô đậm trong Hình 1 là 5x² + 15x + 8.

Bài 5 trang 33 Toán 7 Tập 2:Thực hiện phép chia (9x⁵ – 15x⁴ + 27x³ – 12x²) : 3x².

Lời giải:

Ta thực hiện phép chia đa thức:

(9x⁵ – 15x⁴ + 27x³ – 12x²) : 3x²

= (9x⁵ : 3x²) + (–15x⁴ : 3x²) + (27x³ : 3x²) + (–12x² : 3x²)

= 3x³ – 5x² + 9x – 4

Vậy (9x⁵ – 15x⁴ + 27x³ – 12x²) : 3x² = 3x³ – 5x² + 9x – 4

Bài 6 trang 33 Toán 7 Tập 2:Thực hiện phép chia (2x² – 5x + 3) : (2x – 3).

Lời giải:

Ta thực hiện đặt tính phép chia đa thức:

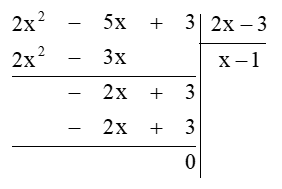
Vậy (2x² – 5x + 3) : (2x – 3) = x – 1.

Bài 7 trang 33 Toán 7 Tập 2:Thực hiện phép chia (4x² – 5) : (x – 2).

Lời giải:

Ta thực hiện đặt tính phép chia đa thức:

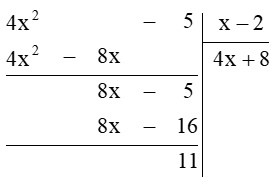
Vậy  $\frac{4x^2-5}{x-2}=4x+8+\frac{11}{x-2}.$

Bài 8 trang 33 Toán 7 Tập 2:Thực hiện phép chia (4x³ – 7x + 2) : (2x² – 3).

Lời giải:

Ta thực hiện đặt tính phép chia đa thức:

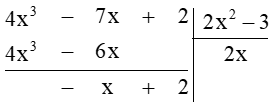
Vậy  $\frac{4x^3-7x+2}{2x^2-3}=2x+\frac{-x+2}{2x^2-3}.$

Bài 9 trang 33 Toán 7 Tập 2:Tính chiều dài của một hình chữ nhật có diện tích bằng 4y² + 4y – 3 (cm²) và chiều rộng bằng (2y – 1) (cm).

Lời giải:

Diện tích của hình chữ nhật bằng tích của chiều dài với chiều rộng.

Do đó chiều dài của hình chữ nhật là thương của phép chia (4y² + 4y – 3) : (2y – 1).

Ta thực hiện đặt tính phép chia đa thức:

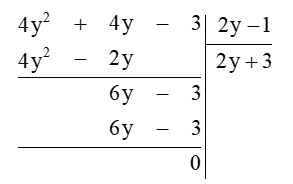
Khi đó: $\frac{4y^2+4y-3}{2y-1}=2y+3.$

Vậy chiều dài của hình chữ nhật là 2y + 3 (cm).

Bài 10 trang 33 Toán 7 Tập 2:Cho hình hộp chữ nhật có thể tích bằng V = 3x³ + 8x² – 45x – 50 (cm³), chiều dài bằng (x + 5) cm và chiều cao (x + 1) cm. Hãy tính chiều rộng của hình hộp chữ nhật.

Lời giải:

Gọi a (cm, a > 0) là chiều rộng của hình hộp chữ nhật.

Khi đó thể tích của hình hộp chữ nhật là:

V = (x + 5) . (x + 1) . a

    = (x² + x + 5x + 5) . a

    = (x² + 6x + 5) . a (cm³)

Mà theo bài hình hộp chữ nhật có thể tích V = 3x³ + 8x² – 45x – 50 (cm³) nên ta có:

(x² + 6x + 5) . a = 3x³ + 8x² – 45x – 50

Suy ra: $a=\frac{3x^3+8x^2-45x-50}{x^2+6x+5}.$

Ta thực hiện đặt tính phép chia đa thức:

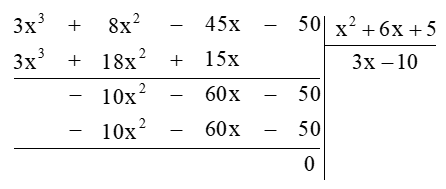
Khi đó  $a=\frac{3x^3+8x^2-45x-50}{x^2+6x+5}=3x-10.$

Vậy chiều rộng của hình hộp chữ nhật là 3x – 10 (cm).

Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 3 : Phép cộng và phép trừ đa thức một biến

Bài 4 : Phép nhân và phép chia đa thức một biến

Bài tập cuối chương 7

Bài 1 : Góc và cạnh của một tam giác

Bài 2 : Tam giác bằng nhau

Lý thuyết Phép nhân và phép chia đa thức một biến

1. Phép nhân đa thức một biến

Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.

Ví dụ 1: Thực hiện phép nhân:

a) 3x. (2x² – 4x + 5);

b) (2x + 3). (x + 1).

Hướng dẫn giải:

a) Ta có: 3x. (2x² – 4x + 5) = 3x. 2x² + 3x. (–4x) + 3x. 5

= 6x³ – 12x + 15x;

b) Ta có: (2x + 3). (x + 1) = 2x. (x + 1) + 3. (x + 1)

= 2x. x + 2x. 1 + 3. x + 3. 1

= 2x² + 2x + 3x + 3

= 2x² + (2x + 3x) + 3

= 2x² + 5x + 3.

2. Phép chia đa thức một biến

Trường hợp 1: Chia đa thức cho đa thức (chia hết)

Cho hai đa thức P và Q (với Q ≠ 0). Ta nói đa thức P chia hết cho đa thức Q nếu có đa thức M sao cho P = Q. M.

Ta gọi P là đa thức bị chia, Q là đa thức chia và M là đa thức thương (gọi tắt là thương).

Kí hiệu M = P : Q hoặc M = $\frac{P}{Q}$.

Ví dụ: Thực hiện phép chia 6x⁶− 8x⁵ + 10x⁴ cho 2x³.

Hướng dẫn giải:

Ta có: (6x⁶ − 8x⁵ + 10x⁴): 2x³

= (6x⁶ : 2x³) – (8x⁵: 2x³) + (10x⁴ : 2x³)

= 3x³ − 4x² + 5x.

Chú ý: Để thực hiện phép chia đa thức, người ta thường viết các đa thức đó thành đa thức thu gọn và sắp xếp các đơn thức theo lũy thừa giảm dần rồi thực hiện phép chia.

Trường hợp 2: Chia đa thức cho đa thức (phép chia có dư)

Khi chia đa thức A cho đa thức B với thương là Q, dư là R thì A = B. Q + R, trong đó bậc của R nhỏ hơn bậc của B.

Ví dụ: Thực hiện phép chia: P(x) = 3x² − 5x + 2 cho Q(x) = x – 2.

Hướng dẫn giải: Thực hiện phép chia, ta được:

Do đó phép chia đa thức P(x) cho Q(x) là phép chia có dư với số dư là 4.

Vậy 3x² − 5x + 2= (x – 2). (3x + 1) + 4.

3. Tính chất của phép nhân đa thức một biến

Tính chất: Cho A, B, C là các đa thức một biến với cùng một biến số.

-Tính chất giao hoán: A. B = B. A;

-Tính chất kết hợp: A. (B. C) = (A. B). C.

Ví dụ: Thực hiện phép tính: 6. (x² – 2).$\frac{1}{2}$;

Hướng dẫn giải:

Ta có: 6. (x² – 2).$\frac{1}{2}$= 6. $\left((x^2-2).\frac{1}{2}\right)=\left(6.\frac{1}{2}\right).(x^2-2)$

= 3. (x² – 2) = 3x² – 6.