Với giải bài 82 trang 33 Toán lớp 8 chi tiết trong Ôn tập chương 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Ôn tập chương 1
Bài 82 trang 33 Toán 8 Tập 1: Chứng minh:
a) x2 – 2xy + y2 + 1 > 0 với mọi số thực x và y.
b) x – x2 – 1 < 0 với mọi số thực x.
Lời giải:
a) Ta có: x2 – 2xy + y2 + 1
= (x2 – 2xy + y2) + 1
= (x – y)2 + 1.
Vì với mọi x, y thuộc R
![]() với mọi số thực x, y
với mọi số thực x, y
b) Ta có:
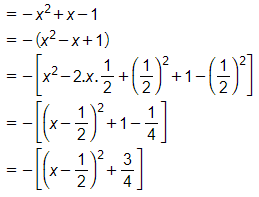
Ta có: với mọi số thực x
với mọi số thực x
với mọi số thực x hay với mọi số thực x (ĐPCM).
Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:
Câu hỏi 2 trang 32 Toán 8 Tập 1: Viết bảy hằng đẳng thức đáng nhớ...
Câu hỏi 3 trang 32 Toán 8 Tập 1: Khi nào thì đơn thức A chia hết cho đơn thức B?...
Câu hỏi 4 trang 32 Toán 8 Tập 1: Khi nào thì đa thức A chia hết cho đơn thức B?...
Câu hỏi 5 trang 32 Toán 8 Tập 1: Khi nào thì đa thức A chia hết cho đa thức B?...
Bài 75 trang 33 Toán 8 Tập 1: Làm tính nhân:...
Bài 76 trang 33 Toán 8 Tập 1: Làm tính nhân:...
Bài 77 trang 33 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức:...
Bài 78 trang 33 Toán 8 Tập 1: Rút gọn các biểu thức sau:...
Bài 79 trang 33 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:...
Bài 80 trang 33 Toán 8 Tập 1: Làm tính chia:...
Bài 81 trang 33 Toán 8 Tập 1: Tìm x, biết:...
Bài 83 trang 33 Toán 8 Tập 1: Tìm để 2n2 – n + 2 chia hết cho 2n + 1...