Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Ôn tập chương 1 hay, chi tiết giúp học sinh dễ dàng làm bài tập Ôn tập chương 1 lớp 8.
Giải bài tập Toán lớp 8 Ôn tập chương 1
Trả lời câu hỏi giữa bài
Lời giải
- Nhân đơn thức với đa thức: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
- Nhân đa thức với đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Câu hỏi 2 trang 32 Toán 8 Tập 1: Viết bảy hằng đẳng thức đáng nhớ.
Lời giải:
Bảy hằng đẳng thức đáng nhớ:
1) (A + B)2 = A2 + 2AB + B2
2) (A – B)2 = A2 – 2AB + B2
3) A2 – B2 = (A – B)(A + B)
4) (A + B)3 = A3 + 3A2B + 3AB2 + B3
5) (A – B)3 = A3 – 3A2B + 3AB2 – B3
6) A3 + B3 = (A + B)(A2 – AB + B2)
7) A3 – B3 = (A – B)(A2 + AB + B2)
Câu hỏi 3 trang 32 Toán 8 Tập 1: Khi nào thì đơn thức A chia hết cho đơn thức B?
Lời giải:
Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
Câu hỏi 4 trang 32 Toán 8 Tập 1: Khi nào thì đa thức A chia hết cho đơn thức B?
Lời giải:
Khi từng hạng tử của đa thức A đều chia hết cho đơn thức B thì đa thức A chia hết cho đơn thức B.
Câu hỏi 5 trang 32 Toán 8 Tập 1: Khi nào thì đa thức A chia hết cho đa thức B?
Lời giải:
Khi đa thức A chia hết cho đa thức B được dư bằng 0 thì ta nói đa thức A chia hết cho đa thức B.
Bài tập (trang 33)
Bài 75 trang 33 Toán 8 Tập 1: Làm tính nhân:
a) 5x2.(3x2 – 7x + 2);
b)
Lời giải:
a) 5x2.(3x2 – 7x + 2)
= 5x2.3x2 - 5x2.7x + 5x2.2
= (5.3).(x2.x2) - 5.7.(x2.x) + (5.2).x2
= 15x2 + 2 - 35.x2 + 1 + 10.x2
= 15x4 – 35x3 + 10x2.
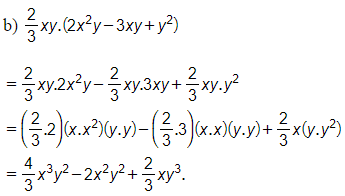
Bài 76 trang 33 Toán 8 Tập 1: Làm tính nhân:
a) (2x2 – 3x)(5x2 – 2x + 1)
b) (x – 2y)(3xy + 5y2 + x)
Lời giải:
a) (2x2 – 3x)(5x2 – 2x + 1)
= 2x2(5x2 – 2x + 1) + (-3x)(5x2 – 2x + 1)
= 2x2.5x2 + 2x2.(-2x) + 2x2.1 + (–3x).5x2 + (-3x).(-2x) + (-3x).1
= (2.5)(x2.x2) + [2. (-2)].(x2.x) + 2x2 + [(-3).5].(x.x2) + [(-3).(-2)].(x.x) + (-3x)
= 10x4 – 4x3 + 2x2 – 15x3 + 6x2 – 3x
= 10x4 – (4x3 + 15x3) + (2x2 + 6x2) – 3x
= 10x4 – 19x3 + 8x2 – 3x
b) (x – 2y)(3xy + 5y2 + x)
= x.(3xy + 5y2 + x) + (-2y).(3xy + 5y2 + x)
= x.3xy + x.5y2 + x.x + (-2y).3xy + (–2y).5y2 + (–2y).x
= 3x2y + 5xy2 + x2 – 6xy2 – 10y3 – 2xy
= 3x2y + (5xy2 – 6xy2) + x2 – 10y3 – 2xy
= 3x2y – xy2 + x2 – 10y3 – 2xy
Bài 77 trang 33 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức:
a) M = x2 + 4y2 – 4xy tại x = 18 và y = 4
b) N = 8x3 – 12x2y + 6xy2 – y3 tại x = 6 và y = - 8
Lời giải:
a) M = x2 + 4y2 – 4xy
= x2 – 2.x.2y + (2y)2 (Hằng đẳng thức (2))
= (x – 2y)2
Thay x = 18, y = 4 vào biểu thức trên, ta được:
M = (18 – 2.4)2 = 102 = 100.
Vậy giá trị biểu thức M tại x = 18 và y = 4 là: 100.
b) N = 8x3 – 12x2y + 6xy2 – y3
= (2x)3 – 3(2x)2y + 3.2xy2 – y3 (Hằng đẳng thức (5))
= (2x – y)3
Thay x = 6, y = - 8 ta được: N = (2.6 – (-8))3 = 203 = 8000.
Vậy giá trị biểu thức N tại x = 6 và y = -8 là 8000.
Bài 78 trang 33 Toán 8 Tập 1: Rút gọn các biểu thức sau:
a) (x + 2)(x – 2) – (x – 3)(x + 1)
b) (2x + 1)2 + (3x – 1)2 + 2(2x + 1)(3x – 1)
Lời giải:
a) (x + 2)(x – 2) – (x – 3)(x + 1)
= x2 – 22 – (x2 + x – 3x – 3)
= x2 – 4 – x2 – x + 3x + 3
= (x2 – x2) + (-x + 3x) + (-4 + 3)
= 2x – 1
b) (2x + 1)2 + (3x – 1)2 + 2(2x + 1)(3x – 1)
= (2x + 1)2 + 2.(2x + 1)(3x – 1) + (3x – 1)2
= [(2x + 1) + (3x – 1)]2
= (2x + 1 + 3x – 1)2
= [(2x + 3x) + (1 – 1)]2
= (5x)2
= 25x2
Bài 79 trang 33 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
a) x2 – 4 + (x – 2)2
b) x3 – 2x2 + x – xy2
c) x3 – 4x2 – 12x + 27
Lời giải:
a) Cách 1: x2 – 4 + (x – 2)2
= (x2– 22) + (x – 2)2 (biểu thức trong ngoặc đầu tiên có dạng hằng đẳng thức số (3))
= (x – 2)(x + 2) + (x – 2)2 (Có nhân tử chung x – 2)
= (x – 2)[(x + 2) + (x – 2)]
= (x – 2)(x + 2 + x – 2)
= (x – 2)(2x)
= 2x(x – 2)
Cách 2: x2 – 4 + (x – 2)2 (Khai triển biểu thức trong ngoặc là hằng đẳng thức (2))
= x2 – 4 + (x2 – 2.x.2 + 22)
= x2 – 4 + x2 – 4x + 4
= 2x2 – 4x (Có nhân tử chung là 2x)
= 2x(x – 2)
b) x3 – 2x2 + x – xy2 (Có nhân tử chung x)
= x(x2 – 2x + 1 – y2) (Có x2 – 2x + 1 là hằng đẳng thức số (1))
= x[(x – 1)2 – y2] (biểu thức trong ngoặc vuông có dạng hằng đẳng thức số (3))
= x(x – 1 + y)(x – 1 – y).
c) x3 – 4x2 – 12x + 27 (Sử dụng phương pháp nhóm hạng tử)
= (x3 + 27) – (4x2 + 12x)
= (x3 + 33) – (4x2 + 12x) (nhóm 1 là HĐT số (6), nhóm 2 có 4x là nhân tử chung)
= (x + 3)(x2 – 3x + 9) – 4x(x + 3)
= (x + 3)(x2 – 3x + 9 – 4x)
= (x + 3)(x2 – 7x + 9)
Bài 80 trang 33 Toán 8 Tập 1: Làm tính chia:
a) (6x3 – 7x2 – x + 2) : (2x + 1)
b) (x4 – x3 + x2 + 3x) : (x2 – 2x + 3)
c) (x2 – y2 + 6x + 9) : (x + y + 3)
Lời giải:
a) Cách 1:Thực hiện phép chia
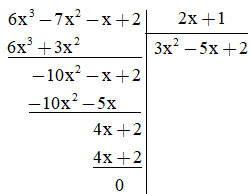
Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2.
Cách 2: Phân tích 6x3 – 7x2 – x + 2 thành (2x + 1).P(x) + R(x)
6x3 – 7x2 – x + 2
= 6x3 + 3x2 – 10x2 – 5x + 4x + 2
(Tách -7x2 = 3x2 – 10x2; -x = -5x + 4x)
= (6x3 + 3x2) – (10x2 + 5x) + (4x + 2)
= 3x2.(2x + 1) – 5x.(2x + 1) + 2.(2x + 1)
= (3x2 – 5x + 2)(2x + 1)
Suy ra P(x) = 3x2 – 5x + 2, R(x) = 0.
Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2
Giải thích cách tách:
Để xuất hiện nhân tử (2x + 1) với số hạng 6x3 ta cần thêm 3x2 để có thể phân tích thành 3x2(2x + 1). Do đó ta tách -7x2 = 3x2 – 10x2.
Lại có -10x2 nên ta cần thêm -5x để có thể phân tích thành -5x(2x + 1). Do đó ta tách –x = -5x + 4x.
Có 4x, ta cần thêm 2 để có 2.(2x + 1) nên 2 không cần phải tách.
b) Cách 1: Thực hiện phép chia
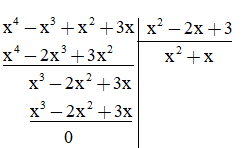
Vậy (x4 – x3 + x2 + 3x) : (x2 – 2x + 3) = x2 + x
Cách 2: Phân tích x4 – x3 + x2 + 3x thành nhân tử có chứa nhân tử x2 – 2x + 3
x4 – x3 + x2 + 3x
= x.(x3 – x2 + x + 3)
= x.(x3 – 2x2 + 3x + x2 – 2x + 3)
= x.[x.(x2 – 2x + 3) + (x2 – 2x + 3)]
= x.(x + 1)(x2 – 2x + 3)
Vậy (x4 – x3 + x2 + 3x) : (x2 – 2x + 3)
= x(x + 1) = x2 + x.
c) Đa thức này không phải đa thức một biến đã sắp xếp nên ta không thực hiện cách chia trực tiếp được.
Phân tích số bị chia thành nhân tử, trong đó có nhân tử là số chia.
(x2 – y2 + 6x + 9) : (x + y + 3)
(Có x2 + 6x + 9 là hằng đẳng thức số (2))
= (x2 + 6x + 9 – y2) : (x + y + 3)
= [(x2 + 2.x.3 + 32) – y2] : (x + y + 3)
= [(x + 3)2 – y2] : (x + y + 3)
(biểu thức trong ngoặc vuông xuất hiện hằng đẳng thức số (3))
= (x + 3 + y)(x + 3 – y) : (x + y + 3)
= x + 3 – y = x – y + 3.
Vậy (x2 – y2 + 6x + 9) : (x + y + 3) = x – y + 3
Bài 81 trang 33 Toán 8 Tập 1: Tìm x, biết:
a)
b) (x + 2)2 – (x – 2)(x + 2) = 0;
c)
Lời giải:
a) (biểu thức trong ngoặc là hằng đẳng thức số (3))
Vậy
b) (x + 2)2 – (x – 2)(x + 2) = 0 (Có x + 2 là nhân tử chung)
⇔ (x + 2)[(x + 2) – (x – 2)] = 0
⇔ (x + 2)(x + 2 – x + 2) = 0
⇔ (x + 2).4 = 0
⇔ x + 2 = 0
⇔ x = - 2
Vậy x = -2
c) (có nhân tử chung là x)
(biểu thức bên trong dấu ngoặc vuông là HĐT số (1))
Vậy
Bài 82 trang 33 Toán 8 Tập 1: Chứng minh:
a) x2 – 2xy + y2 + 1 > 0 với mọi số thực x và y.
b) x – x2 – 1 < 0 với mọi số thực x.
Lời giải:
a) Ta có: x2 – 2xy + y2 + 1
= (x2 – 2xy + y2) + 1
= (x – y)2 + 1.
Vì với mọi x, y thuộc R
![]() với mọi số thực x, y
với mọi số thực x, y
b) Ta có:
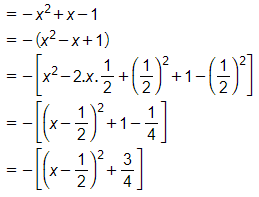
Ta có: với mọi số thực x
với mọi số thực x
với mọi số thực x hay với mọi số thực x (ĐPCM).
Bài 83 trang 33 Toán 8 Tập 1: Tìm để 2n2 – n + 2 chia hết cho 2n + 1.
Lời giải:
Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
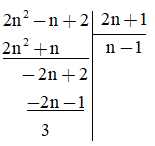
Để 2n2 – n + 2 chia hết cho 2n + 1
hay (2n + 1) Ư(3) = {-3; -1; 1; 3}.
Ta có bảng sau:
|
2n + 1 |
-3 |
-1 |
1 |
3 |
|
n |
-2 |
-1 |
0 |
1 |
Vậy