Để tìm đa thức \(P\left( x \right)\) bậc không quá n khi biết giá trị tại \(\left( {n + 1} \right)\) điểm:

\({C_1};{C_2};....;{C_{n + 1}}\) ta có thể biểu diễn \(P\left( x \right)\) dưới dạng:

\[P\left( x \right) = {b_0} + {b_1}\left( {x - {C_1}} \right) + {b_2}\left( {x - {C_1}} \right)\left( {x - {C_2}} \right) + ...... + {b_n}\left( {x - {C_1}} \right)\left( {x - {C_2}} \right)....\left( {x - {C_n}} \right).\]                       

Bằng cách thay thế x lần lượt bằng các giá trị \({C_1};{C_2};....;{C_{n + 1}}\) vào biểu thức P(x) ta lần lượt tính được các hệ số \({b_0};{b_1};....;{b_n}\)

7. Lược đồ Horner.

Horner là nhà toán học Anh. Ông sinh năm 1787, mất năm 1837. Ông không có nhiều công trình nhưng nổi tiếng vì một phương pháp tính gần đúng một số phương trình và bây giờ lấy tên ông đặt cho phương pháp ấy. Thực ra thuật toán đã được người Trung Hoa biết đến từ trước, nhưng Horner đã phát minh ra nó một cách độc lập. Sau đây là lược đồ Horner:

Để tìm thương và dư trong phép chia \(f\left( x \right) = {a_0}{x^n} + {a_1}{x^{n - 1}} + ... + {a_{n - 1}}{x^{ + a}}\) \(\left( {{a_0} \ne 0} \right)\) cho \(g\left( x \right) = x - \alpha \). Ta lập bảng:

Với

 \(\begin{array}{l}f\left( x \right) = \left( {x - \alpha } \right)q\left( x \right) + f\left( x \right);\\f\left( x \right) = {b_n} = a{b_{n - 1}} + {a_n}\end{array}\)

\(q\left( x \right) = {b_0}{x^{n - 1}} + {b_1}{x^{n - 2}} + ... + {b_{n - 2}}x + {b_{n - 1}}\)

II. Một số ví dụ

Ví dụ 1: Thực hiện phép chia \(A:B\) trong các trường hợp sau:

a) \(A = 12{x^3}{y^4}\); \(B =  - 3{x^2}y\).

b) \(A =  - \frac{{10}}{3}{x^6}{y^5}{z^2}\); \(B = \frac{1}{9}{x^2}yz\).

c) \(A = \left( { - \frac{1}{2}{x^n}{y^{n + 2}}} \right):\left( {3{x^{n - 2}}{y^n}} \right)\) \(\left( {n \in \mathbb{N},\,n \ge 2} \right)\).

Giải

a) \(A:B = 12{x^3}{y^4}:\left( { - 3{x^2}y} \right) =  - 4x{y^3}\);

b)

 \(\begin{array}{l}A:B = \left( { - \frac{{10}}{3}{x^6}{y^5}{z^2}} \right):\left( {\frac{1}{9}{x^2}yz} \right)\\ =  - 30{x^4}{y^4}z\end{array}\);

c)

 \(\begin{array}{l}A:B = \left( { - \frac{1}{2}{x^n}{y^{n + 2}}} \right):\left( {3{x^{n - 2}}{y^n}} \right)\\ = \frac{1}{6}{x^2}{y^2}\end{array}\).

Ví dụ 2: Chứng minh rằng:

a) \({x^8} + {x^4} + 1 \vdots {x^2} + x + 1\)

b) \({x^5} + {x^4} + 1 \vdots {x^2} + x + 1\)

Giải

Tìm cách giải. Khi chứng minh đa thức \(f\left( x \right) \vdots g\left( x \right)\) ta có thể:

- Cách 1. Phân tích đa thức \(f\left( x \right)\) thành nhân tử có chứa nhân tử \(g\left( x \right)\).

- Cách 2. Biến đổi đa thức \(f\left( x \right)\) thành tổng các đa thức chia hết cho đa thức \(g\left( x \right)\).

Trình bày lời giải

a) Cách 1. Ta có:

\({x^8} + {x^4} + 1 = {x^8} + 2{x^4} + 1 - {x^4} = {\left( {{x^4} + {x^2}} \right)^2} - {x^4}\)

\( = \left( {{x^4} + 1 - {x^2}} \right)\left( {{x^4} + 1 + {x^2}} \right)\)

\( = \left( {{x^4} - {x^2} + 1} \right)\left( {{x^4} + 2{x^2} + 1 - {x^2}} \right)\)

\( = \left( {{x^4} - {x^2} + 1} \right)\left[ {{{\left( {{x^2} + 1} \right)}^2} - {x^2}} \right]\)

\( = \left( {{x^4} - {x^2} + 1} \right)\left( {{x^2} + 1 - x} \right)\left( {{x^2} + 1 + x} \right) \vdots \left( {{x^2} + x + 1} \right)\)

\( \Rightarrow {x^8} + {x^4} + 1 \vdots {x^2} + x + 1\)

Cách 2.

\({x^8} + {x^4} + 1 = {x^8} - {x^2} + {x^4} - x + {x^2} + x + 1\)

\( = {x^2}\left( {{x^6} - 1} \right) + x\left( {{x^3} - 1} \right) + \left( {{x^2} + x + 1} \right)\)

\( = {x^2}\left( {{x^3} + 1} \right)\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) + x\left( {{x^2} - 1} \right)\left( {{x^2} + x + 1} \right) + \left( {{x^2} + x + 1} \right) \vdots {x^2} + x + 1\)

b) \({x^5} + {x^4} + 1 = {x^5} + {x^4} + {x^3} - {x^3} + 1 = {x^3}\left( {{x^2} + x + 1} \right) - \left( {x - 1} \right)\left( {{x^2} + x + 1} \right)\)

\( = \left( {{x^2} + x + 1} \right)\left( {{x^3} - x + 1} \right) \vdots \left( {{x^2} + x + 1} \right)\) .

Ví dụ 3: Tìm các số thực a, b, sao cho đa thức \(4{x^4} - 11{x^3} - 2a{x^2} + 5bx - 6\) chia hết cho đa thức \({x^2} - 2x - 3\).

(Thi học sinh giỏi lớp 9, TP Hà Nội, năm học 2012 - 2013)

Giải

Tìm cách giải. Khi tìm hệ số a, b sao cho đa thức \(f\left( x \right)\) chia hết cho đa thức \(g\left( x \right)\), chúng ta có hai hướng suy nghĩ:

Đặt phép chia \(f\left( x \right)\) cho \(g\left( x \right)\) đến khi được phần dư có bậc nhỏ hơn bậc của đa thức \(g\left( x \right)\). Để phép chia hết ta đồng nhất phần dư đó với đa thức 0.

Còn nếu đa thức \(g\left( x \right)\) phân tích được thành nhân tử với các nhân tử bậc nhất, ta viết \(f\left( x \right)\) thành tích các nhân tử đó nhân với đa thức thương. Rồi dùng đồng nhất thức sao cho vế phải bằng 0.

Trình bày lời giải

Cách 1. Thực hiện phép chia ta được:

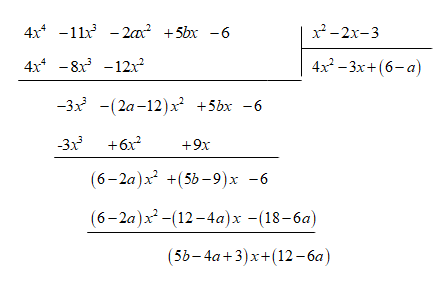
Để phép chia hết thì

\(\left\{ \begin{array}{l}5b - 4a + 3 = 0\\12 - 6a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 1\end{array} \right.\)

Cách 2. Ta có:

 \({x^2} - 2x - 3 = {x^2} - 2x + 1 - 4 = {\left( {x - 1} \right)^2} - 4\)

\( = \left( {x - 1 - 1} \right)\left( {x - 1 + 2} \right) = \left( {x - 3} \right)\left( {x + 1} \right)\)

Đặt thương là \(q\left( x \right)\) ta có:

 \(4{x^4} - 11{x^3} - 2a{x^2} + 5bx - 6 = \left( {x - 3} \right)\left( {x + 1} \right)q\left( x \right)\)

Chọn \(x = 3\) ta có:

\({4.3^4} - {11.3^3} - 2a{.3^2} + 5.b.3 - 6 = 0\)

\( \Rightarrow 15b - 18a =  - 21 \Rightarrow 5b - 6a =  - 7\) (1)

Chọn \(x =  - 1\) ta có:

 \(4.{\left( { - 1} \right)^4} - 11.{\left( { - 1} \right)^3} - 2a.{\left( { - 1} \right)^2} + 5.b.\left( { - 1} \right) - 6 = 0\)

\( \Rightarrow 5b + 2a = 9\) (2)

Từ (1) và (2) suy ra:

 \(8a = 16 \Rightarrow a = 2\)

Thay vào (2) \( \Rightarrow 5.b + 4 = 9 \Rightarrow b = 1\).

Ví dụ 4: Tìm đa thức \(f\left( x \right)\) biết:

\(f\left( x \right)\) chia cho \(x + 3\) dư 1 ;

\(f\left( x \right)\) chia cho \(x - 4\) dư 8;

\(f\left( x \right)\) chia cho \(\left( {x + 3} \right)\left( {x - 4} \right)\) thì được \(3x\) và còn dư.

Giải

Tìm cách giải. Ta có \(\left( {x + 3} \right)\left( {x - 4} \right)\) là tam thức bậc hai, do đó phần dư khi chia \(f\left( x \right)\) chia cho \(\left( {x + 3} \right)\left( {x - 4} \right)\) có dạng tổng quát là \(ax + b\). Từ đó suy ra được: \(f\left( x \right) = \left( {x + 3} \right)\left( {x - 4} \right)3x + ax + b\). Mặt khác ta có \(f\left( { - 3} \right) = 1,\,f\left( 4 \right) = 8\). Do vậy để tìm \(f\left( x \right)\) chúng ta cần xác định a. b bằng cách chọn \(x =  - 3;x = 4\) để đồng nhất hai vế.

Trình bày lời giải

Theo định lý Bézout ta có \(f\left( 3 \right) = 1,\,f\left( 4 \right) = 8\)

Đặt dư \(f\left( x \right)\) chia cho \(\left( {x + 3} \right)\left( {x - 4} \right)\) là \(ax + b\)

Suy ra \(f\left( x \right) = \left( {x + 3} \right)\left( {x - 4} \right) + ax + b\).

Với \(x =  - 3\) tacó:

 \(\begin{array}{l} = \left( { - 3 + 3} \right)\left( { - 3 - 4} \right).3.\left( { - 3} \right) + a\left( { - 3} \right) + b\\ \Rightarrow b - 3a = 1\,(1)\end{array}\)

Với \(x = 4\) ta có:

 \(\begin{array}{l}8 = \left( {4 + 3} \right)\left( {4 - 4} \right)\left( {3.4} \right) + a.4 + b\\ \Rightarrow b + 4a = 8\,(2)\end{array}\)

Từ (1 ) và (2) suy ra: \(7a = 7 \Rightarrow a = 1\) thay vào (2) ta được \(b = 4\).

Từ đó ta được:

 \(f\left( x \right) = \left( {x + 3} \right)\left( {x - 4} \right)3x + x + 4\)

Hay \(f\left( x \right) = 3{x^3} - 3{x^2} - 35x + 4\)

Ví dụ 5: Tìm một đa thức bậc ba, biết P(x) chia cho \(\left( {x - 1} \right),\,\,\left( {x - 2} \right),\,\,\left( {x - 3} \right)\) đều được dư 6 và \(P\left( { - 1} \right) =  - 18\).

Giải

Tìm cách giải. Từ đề bài theo định lí Bézout ta có \(P\left( 1 \right) = 6,P\left( 2 \right) = 6,P\left( 3 \right) = 6,P\left( { - 1} \right) =  - 18\). Như vậy đa thức P(x) bậc ba mà biết giá trị tại bốn điểm 1; 2; 3; - 1 nên ta có thể sử dụng phương pháp nội suy Newton.

Trình bày lời giải

Theo định lý Bézout ta có: \(P\left( 1 \right) = P\left( 2 \right),\,P\left( 3 \right) = 6\).

Do đó ta đặt

\(P\left( x \right) = d + c\left( {x - 1} \right) + b\left( {x - 1} \right)\left( {x - 2} \right) + a\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)\)

Cho \(x = 1\) ta được \(P\left( 1 \right) = d\), suy ra \[d = 6\]

\(P\left( x \right) = 6 + c\left( {x - 1} \right) + b\left( {x - 1} \right)\left( {x - 2} \right) + a\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)\)

Cho \(x = 2\) ta được \(P\left( 2 \right) = 6 + c\), suy ra \[c = 0\]

\(P\left( x \right) = 6 + 0\left( {x - 1} \right) + b\left( {x - 1} \right)\left( {x - 2} \right) + a\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)\)

Cho \(x = 3\) ta được \(P\left( 3 \right) = 6 + 2b\), suy ra \[b = 0\]

\(P\left( x \right) = 6 + 0\left( {x - 1} \right) + 0\left( {x - 1} \right)\left( {x - 2} \right) + a\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)\)

Do đó \(P\left( x \right) = 6 + a\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)\).

Cho \(x =  - 1\) ta được \(P\left( { - 1} \right) = 6 - 24a\), do đó \( - 18 = 6 - 24a\) suy ra \(a = 1\).

Vậy \(P\left( x \right) = 6 + 1.\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)\)

Rút gọn ta được: \(P\left( x \right) = {x^3} - 6{x^2} + 11x\).

Ví dụ 6: Chứng minh rằng đa thức \(f\left( x \right) = {\left( {x - 3} \right)^{200}} + {\left( {x - 2} \right)^{100}} - 1\) chia hết cho đa thức \(g\left( x \right) = {x^2} - 5x + 6\)

Giải

Tìm cách giải. Đa thức \(g\left( x \right)\) bậc n có n nghiệm phân biệt. Nếu mọi nghiệm của đa thức \(g\left( x \right)\) cũng là nghiệm của đa thức \(f\left( x \right)\) thì đa thức \(f\left( x \right)\) chia hết cho đa thức \(g\left( x \right)\). Nhận thấy trong bài \(g\left( x \right)\) có hai nghiệm là \(x = 2;x = 3\), nên chúng ta chỉ cần kiểm tra xem \(x = 2;x = 3\) có là nghiệm của \(f\left( x \right)\) không?

Trình bày lời giải

Ta có: \(f\left( 2 \right) = {\left( {2 - 3} \right)^{200}} + {\left( {2 - 2} \right)^{100}} - 1\) nên \(f\left( x \right) \vdots \left( {x - 2} \right)\)

\(f\left( 3 \right) = {\left( {3 - 3} \right)^{200}} + {\left( {3 - 2} \right)^{100}} - 1\) nên \(f\left( x \right) \vdots \left( {x - 3} \right)\)

Nên \(f\left( x \right)\) chia hết cho \(\left( {x - 2} \right)\left( {x - 3} \right) = {x^2} - 5x + 6\)