Với giải Bài 11 trang 64 Toán 12 Tập 2 Cánh diều chi tiết trong Bài 1: Phương trình mặt phẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 1: Phương trình mặt phẳng

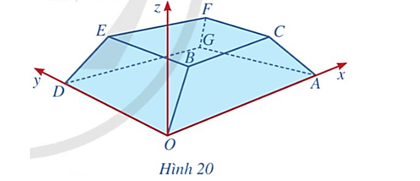
Bài 11 trang 64 Toán 12 Tập 2: Hình 20 minh họa hình ảnh một tòa nhà trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là mét). Biết A(50; 0; 0), D(0; 20; 0), B(4k; 3k; 2k) với k > 0 và mặt phẳng (CBEF) có phương trình là z = 3.

a) Tìm tọa độ của điểm B.

b) Lập phương trình mặt phẳng (AOBC).

c) Lập phương trình mặt phẳng (DOBE).

d) Chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng (AOBC) và (DOBE).

Lời giải:

a) Vì B ∈ (CBEF) nên ta có 2k = 3, suy ra k = $\frac{3}{2}$ (tm). Do đó, 4k = 6; 3k = $\frac{9}{2}$.

Vậy $B\left(6;\frac{9}{2};3\right)$.

b) Ta có $\overrightarrow{OA}=\left(50;0;0\right),\overrightarrow{OB}=\left(6;\frac{9}{2};3\right)$.

Xét vectơ $\overrightarrow{n}=\left[\overrightarrow{OA},\overrightarrow{OB}\right]=\left(\left|\begin{array}{cc}0& 0\\ \frac{9}{2}& 3\end{array}\right|;\left|\begin{array}{cc}0& 50\\ 3& 6\end{array}\right|;\left|\begin{array}{cc}50& 0\\ 6& \frac{9}{2}\end{array}\right|\right)$, tức là $\overrightarrow{n}=\left(0;-150;225\right)$.

Khi đó, $\overrightarrow{n}$ là vectơ pháp tuyến của mặt phẳng (AOBC).

Vậy mặt phẳng (AOBC) có phương trình là:

0(x – 0) – 150(y – 0) + 225(z – 0) = 0 ⇔ 2y – 3z = 0.

c) Ta có $\overrightarrow{OD}=\left(0;20;0\right),\overrightarrow{OB}=\left(6;\frac{9}{2};3\right)$.

Xét vectơ $\overrightarrow{n^{\text{'}}}=\left[\overrightarrow{OD},\overrightarrow{OB}\right]=\left(\left|\begin{array}{cc}20& 0\\ \frac{9}{2}& 3\end{array}\right|;\left|\begin{array}{cc}0& 0\\ 3& 6\end{array}\right|;\left|\begin{array}{cc}0& 20\\ 6& \frac{9}{2}\end{array}\right|\right)$ , tức là $\overrightarrow{n^{\text{'}}}=\left(60;0;-120\right)$.

Khi đó, $\overrightarrow{n^{\text{'}}}$ là vectơ pháp tuyến của mặt phẳng (DOBE).

Vậy mặt phẳng (DOBE) có phương trình là:

60(x – 0) + 0(y – 0) – 120(z – 0) = 0 ⇔ x – 2z = 0.

d) Một vectơ pháp tuyến của mặt phẳng (AOBC) là $\overrightarrow{n_1}=\left(0;2;-3\right)$.

Một vectơ pháp tuyến của mặt phẳng (DOBE) là $\overrightarrow{n_2}=\left(1;0;-2\right)$