Với tóm tắt lý thuyết Toán lớp 9 Bài 1: Căn bậc hai và căn bậc ba của số thực sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực

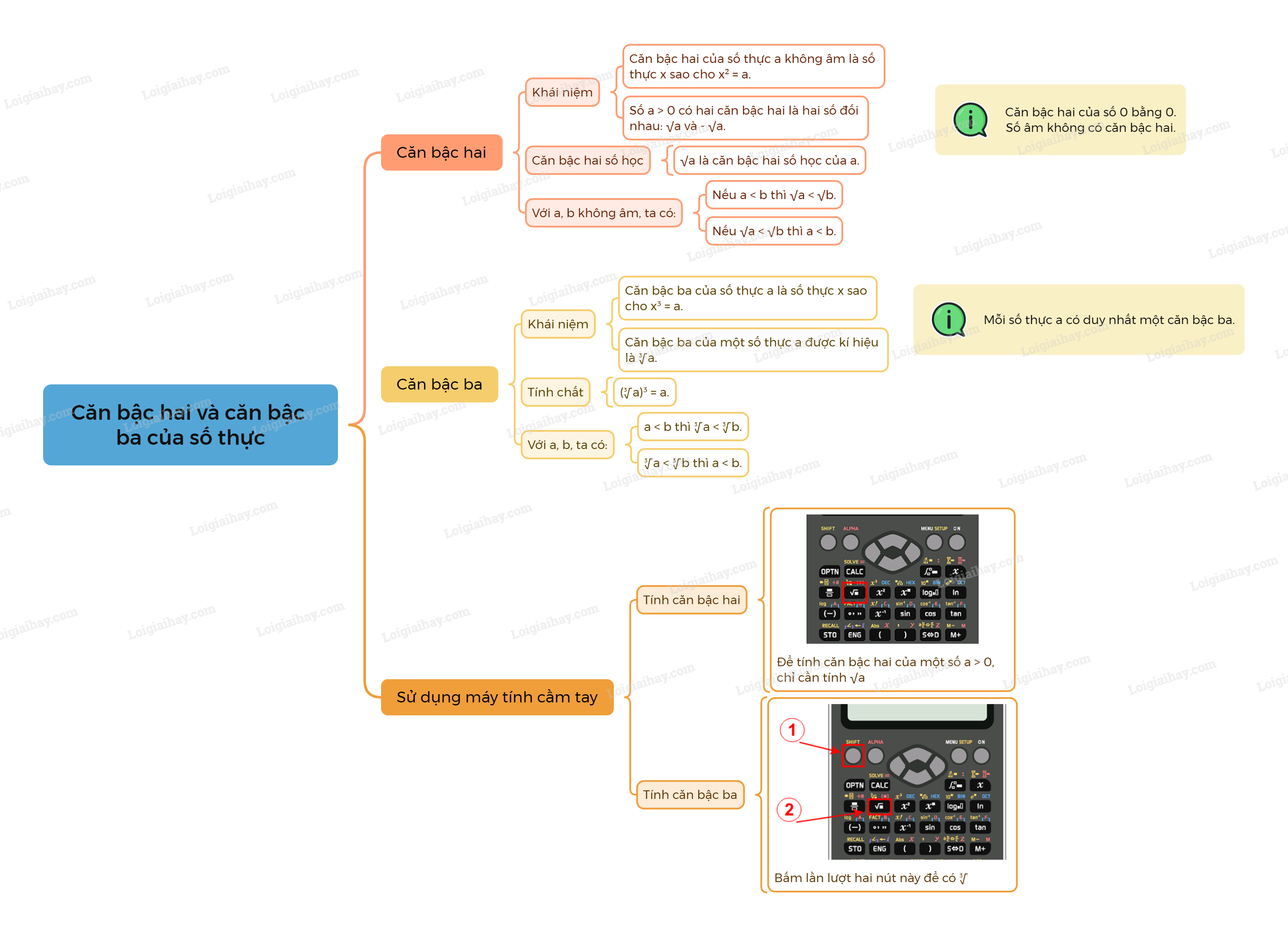
A. Lý thuyết Căn bậc hai và căn bậc ba của số thực

1. Căn bậc hai của số thực không âm

Chú ý:

- Khi $a>0$, số a có đúng hai căn bậc hai là hai số đối nhau: số dương kí hiệu là $\sqrt{a}$; số âm kí hiệu là $-\sqrt{a}$. Ta gọi $\sqrt{a}$ là căn bậc hai số học của a.

- Căn bậc hai của số 0 bằng 0.

- Số âm không có căn bậc hai.

Ví dụ:

· $\sqrt{81}=9$ nên 81 có hai căn bậc hai là 9 và -9.

· Căn bậc hai số học của 121 là $\sqrt{121}=11$.

Nhận xét: Với hai số a, b không âm, ta có:

- Nếu $a<b$ thì $\sqrt{a}<\sqrt{b}$;

- Nếu $\sqrt{a}<\sqrt{b}$ thì $a<b$.

2. Căn bậc ba

Khái niệm căn bậc ba của một số thực

Chú ý: Mỗi số thực a đều có duy nhất một căn bậc ba.

Nhận xét: ${\left(\sqrt[3]{a}\right)}^3=a$.

Với hai số a, b, ta có:

- Nếu $a<b$ thì $\sqrt[3]{a}<\sqrt[3]{b}$.

- Nếu $\sqrt[3]{a}<\sqrt[3]{b}$ thì $a<b$.

Ví dụ:

$\sqrt[3]{64}=\sqrt[3]{4^3}=4$;

$\sqrt[3]{-27}=\sqrt[3]{{\left(-3\right)}^3}=-3$.

3. Sử dụng máy tính cầm tay để tìm căn bậc hai, căn bậc ba của một số hữu tỉ

Tính căn bậc hai của một số bằng máy tính cầm tay

Tính căn bậc ba của một số bằng máy tính cầm tay

Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.

Ví dụ:

Sơ đồ tư duy Căn bậc hai và căn bậc ba của số thực

B. Bài tập Căn bậc hai và căn bậc ba của số thực

Bài 1. Số nào sau đây là căn bậc hai của 100?

A. 10;

B. –10;

C. 50;

D. –10 và 10.

Hướng dẫn giải

Đáp án đúng là: D

Ta có: 10² = 100 và (–10)² = 100 nên số 10 và –10 là căn bậc hai của 100.

Bài 2. Số 25 là căn bậc hai của số nào sau đây?

A. 5;

B. 12,5;

C. 625;

D. Một đáp án khác.

Hướng dẫn giải

Đáp án đúng là: C

Ta có 25² = 625 nên 25 là căn bậc hai của số 625.

Bài 3.Khẳng định nào sau đây đúng?

A. $\sqrt[3]{a}=x$ nếu a³ = x;

B. $\sqrt[3]{a}=-x$ nếu a³ = x;

C. $\sqrt[3]{a}=x$ nếu a = x³;

D. $\sqrt[3]{a}=-x$ nếu a = x³.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: $\sqrt[3]{a}=x$ nếu a = x³.

Bài 4. Tính giá trị của các biểu thức sau:

a) ${\left(\sqrt{58}\right)}^2-\sqrt{{45}^2}$

b) $\frac{2}{7}\sqrt{49}+\frac{26}{3}\sqrt{\frac{81}{169}}-\sqrt{625}$

c) $\sqrt[3]{{\left(-15\right)}^3}+{\left(\sqrt[3]{21}\right)}^3-\sqrt[3]{-27}$

d) $\left(\sqrt{2030}-\sqrt{2029}\right)\left(\sqrt{2030}+\sqrt{2029}\right)$

e) $\left(\sqrt[3]{3}-1\right)\left[{\left(\sqrt[3]{3}\right)}^2+\sqrt[3]{3}+1\right].$

Hướng dẫn giải

a) ${\left(\sqrt{58}\right)}^2-\sqrt{{45}^2}=58-45=13$

b) $\frac{2}{7}\sqrt{49}+\frac{26}{3}\sqrt{\frac{81}{169}}-\sqrt{625}$

= $=\frac{2}{7}·7+\frac{26}{3}·\frac{9}{13}-25$

= 2 + 6 – 25

= –17.

c) $\sqrt[3]{{\left(-15\right)}^3}+{\left(\sqrt[3]{21}\right)}^3-\sqrt[3]{-27}$

= –15 + 21 – 3

= 3.

d) $\left(\sqrt{2030}-\sqrt{2029}\right)\left(\sqrt{2030}+\sqrt{2029}\right)$

= 2 030 – 2 029 = 1.

e) $\left(\sqrt[3]{3}-1\right)\left[{\left(\sqrt[3]{3}\right)}^2+\sqrt[3]{3}+1\right]={\left(\sqrt[3]{3}\right)}^3-1^3=3-1=2.$

Bài 5.Người ta cần làm một cái thùng hình lập phương bằng bìa cứng không có nắp trên và có thể tích 32768 m³. Tính diện tích bìa cứng cần dùng để làm thùng đựng đó (coi diện tích các mép nối là không đáng kể).

Hướng dẫn giải

Cạnh cái thùng hình lập phương là: $\sqrt[3]{32768}=32$(m).

Cái thùng đó có 5 mặt là 5 hình vuông.

Diện tích bìa cứng phải dùng để làm cái thùng là:

32². 5 = 5 120 (m²).

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 2: Bất phương trình bậc nhất một ẩn

Lý thuyết Bài 1: Căn bậc hai và căn bậc ba của số thực

Lý thuyết Bài 2: Một số phép tính về căn bậc hai của số thực

Lý thuyết Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

Lý thuyết Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Lý thuyết Bài 1: Tỉ số lượng giác của góc nhọn