Với tóm tắt lý thuyết Toán lớp 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

A. Lý thuyết Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

1. Căn thức bậc hai

Khái niệm căn thức bậc hai

Ví dụ: $\sqrt{2x-1}$, $\sqrt{-\frac{1}{3}{x}^2+2}$ là các căn thức bậc hai.

Điều kiện xác định của căn thức bậc hai

Ví dụ: Điều kiện xác định của căn thức $\sqrt{2x+1}$ là $2x+1\ge 0$ hay $x\ge -\frac{1}{2}$.

Điều kiện xác định của căn thức $\sqrt{-\frac{1}{3}x+2}$ là $-\frac{1}{3}x+2\ge 0$ hay $x\le 6$.

2. Căn thức bậc ba

Khái niệm căn thức bậc ba

Chú ý: Các số, biến số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, khai căn (bậc hai hay bậc ba) làm thành một biểu thức đại số.

Ví dụ: $\sqrt[3]{x}$, $\sqrt[3]{\frac{1}{x+1}}$ là các căn thức bậc ba.

Điều kiện xác định của căn thức bậc ba

Ví dụ:

$\sqrt[3]{5x-11}$ xác định với mọi số thực x vì $5x-11$ xác định với mọi số thực x.

$\sqrt[3]{\frac{1}{x-1}}$ xác định với $x\ne 1$ vì $\frac{1}{x-1}$ xác định với $x\ne 1$.

Sơ đồ tư duy Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

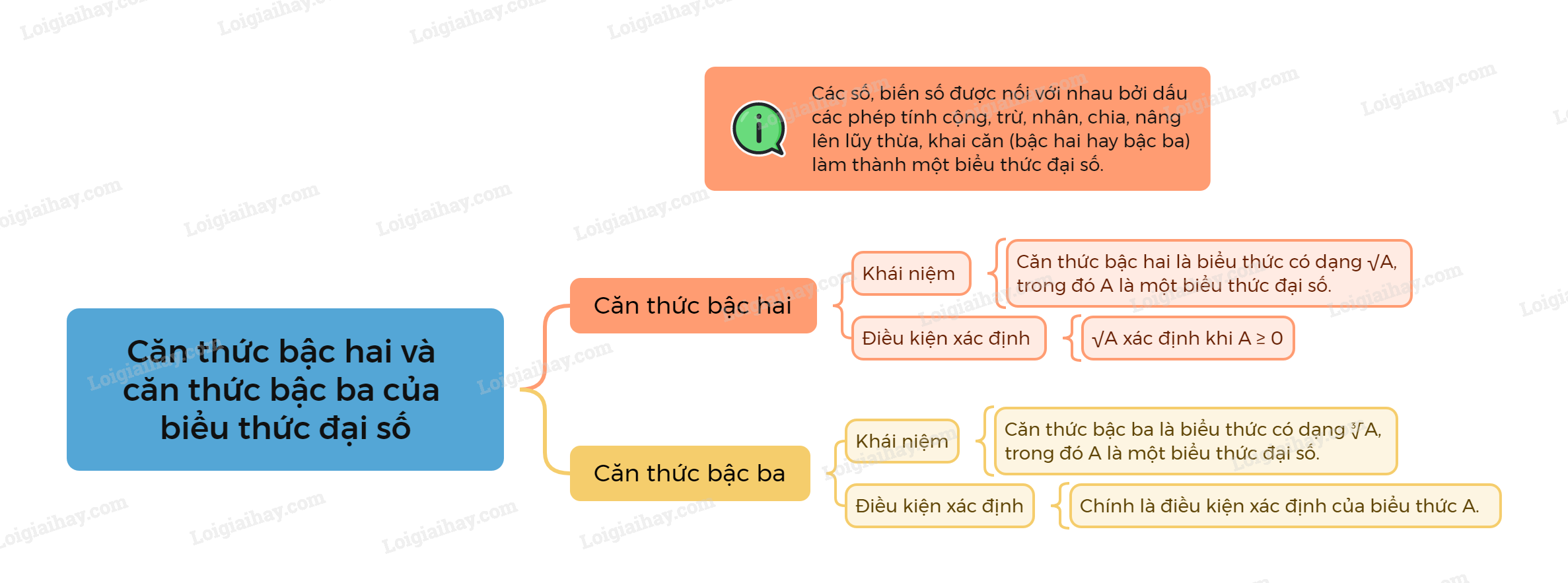
B. Bài tập Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

Bài 1.Biểu thức $\sqrt[3]{16\text{x}-5}$ có nghĩa khi

A. $x\ne \frac{5}{16};$

B. $x\ge \frac{5}{16};$

C. $x\le \frac{5}{16};$

D. x là số thực.

Hướng dẫn giải

Đáp án đúng là: D

$\sqrt[3]{16\text{x}-5}$ xác định với mọi số thực x vì 16x – 5 xác định với mọi số thực x.

Bài 2.Biểu thức $\sqrt{\frac{{\left(-5\right)}^2}{6-3\text{x}}}$ có nghĩa khi:

A. x < 2;

B. x > 2;

C. x ≤ 2;

D. x ≥ 2.

Hướng dẫn giải

Đáp án đúng là: A

Biểu thức $\sqrt{\frac{{\left(-5\right)}^2}{6-3\text{x}}}$ có nghĩa khi 6 – 3x ≠ 0 và $\frac{{\left(-5\right)}^2}{6-3\text{x}}\ge 0.$

⦁6 – 3x ≠ 0, hay 3x ≠ 6 nên x ≠ 2;

⦁ $\frac{{\left(-5\right)}^2}{6-3\text{x}}\ge 0$ khi 6 – 3x > 0 (vì (–5)² > 0), hay 3x < 6 nên x < 2.

Kết hợp hai điều kiện trên ta được x < 2.

Vậy biểu thức $\sqrt{\frac{{\left(-5\right)}^2}{6-3\text{x}}}$ có nghĩa khi x < 2.

Bài 3. Có bao nhiêu số tự nhiên x để $\sqrt{16-x}$ là số nguyên?

A. 2;

B. 3;

C. 4;

D. 5.

Hướng dẫn giải

Đáp án đúng là: D

Biểu thức $\sqrt{16-x}$ có nghĩa thì 16 – x ≥ 0.

Mà x là số tự nhiên nên x ≥ 0, suy ra 16 – x ≤ 16.

Do đó 0 ≤ 16 – x ≤ 16. (1)

Để $\sqrt{16-x}$ là số nguyên thì 16 – x phải là số chính phương.

Từ (1) và (2) suy ra 16 – x ∈ {0; 1; 4; 9; 16}.

Do đó x – 16 ∈ {0; –1; –4; –9; –16}

Nên x ∈ {16; 15; 12; 7; 0}.

Vậy có 5 giá trị của x thỏa mãn yêu cầu đề bài.

Bài 4. Tìm điều kiện xác định của các biểu thức sau:

a) $\sqrt{3x-36};$

b) $\sqrt{24-3x};$

c) $\sqrt{\frac{2}{x^2}};$

d) $\sqrt{\frac{3}{1-2x}};$

e) $\sqrt{\frac{-10}{2x+4}};$

f) $\sqrt[3]{5-x};$

g) $\sqrt[3]{\frac{1}{x-1}};$

h) $\sqrt[3]{\frac{x-2}{-x^2+x-1}}.$

Hướng dẫn giải

a) Biểu thức $\sqrt{3x-36}$ xác định khi 3x – 36 ≥ 0 hay 3x ≥ 36, tức là x ≥ 12.

b) Biểu thức $\sqrt{24-3x}$xác định khi 24 – 3x ≥ 0 hay 3x ≤ 24, tức là x ≤ 8.

c) Biểu thức $\sqrt{\frac{2}{x^2}}$xác định khi $\frac{2}{x^2}\ge 0,$ hay x² > 0, tức là x ≠ 0.

d) Biểu thức $\sqrt{\frac{3}{1-2x}}$xác định khi $\frac{3}{1-2x}\ge 0,$ hay 1 – 2x > 0, tức là

e) Biểu thức $\sqrt{\frac{-10}{2x+4}}$xác định khi $\frac{-10}{2x+4}\ge 0,$ hay 2x + 4 < 0, tức là x < –2.

f) Biểu thức $\sqrt[3]{5-x}$xác định với mọi số thực x vì 5 – x xác định với mọi số thực x.

g) Biểu thức $\sqrt[3]{\frac{1}{x-1}}$xác định khi $\frac{1}{x-1}$ xác định, có nghĩa là x – 1 ≠ 0, hay x ≠ 1.

h) Biểu thức $\sqrt[3]{\frac{x-2}{-x^2+x-1}}$xác định khi $\frac{x-2}{-x^2+x-1}$ xác định, có nghĩa là –x² + x – 1 ≠ 0.

Ta có: $-x^2+x-1=-\left(x^2-2\cdot x\cdot \frac{1}{2}+\frac{1}{4}\right)-\frac{3}{4}=-{\left(x-\frac{1}{2}\right)}^2-\frac{3}{4}.$

Với mọi số thực x, ta có ${\left(x-\frac{1}{2}\right)}^2\ge 0,$ nên $-{\left(x-\frac{1}{2}\right)}^2\le 0,$ suy ra $-{\left(x-\frac{1}{2}\right)}^2-\frac{3}{4}\le -\frac{3}{4}$

Do đó $-{\left(x-\frac{1}{2}\right)}^2-\frac{3}{4}\ne 0$ với mọi số thực x hay biểu thức $\sqrt[3]{\frac{x-2}{-x^2+x-1}}$ xác định với mọi số thực x.

Bài 5.Công thức $h=0,4\sqrt[3]{x}$ biểu diễn mối tương quan giữa cân nặng x (tính bằng kg) và chiều cao h (tính bằng m) của một con hươu cao cổ.

a) Một con hươu cao cổ cân nặng 195 kg thì cao bao nhiêu mét? (làm tròn kết quả đến hàng phần trăm).

b) Một con hươu cao cổ có chiều cao 2,62 m thì cân nặng bao nhiêu kilôgam? (làm tròn kết quả đến hàng đơn vị).

Hướng dẫn giải

a) Con hươu cao cổ nặng 195 kg thì x = 195.

Thay x = 195 vào công thức $h=0,4\sqrt[3]{x}$ ta được chiều cao của con hươu cao cổ là:

$h=0,4\sqrt[3]{x}=0,4\sqrt[3]{195}\approx 2,32$ (m).

b) Con hươu cao cổ cao 2,62 m thì h = 2,62.

Thay h = 2,62vào công thức $h=0,4\sqrt[3]{x}$ ta được phương trình:

$2,62=0,4\sqrt[3]{x}.$

Giải phương trình:

$2,62=0,4\sqrt[3]{x}.$

$\sqrt[3]{x}=6,55$

x ≈ 281 (kg).

Vậy con hươu cao cổ có chiều cao 2,62 m thì cân nặng khoảng 281kg.

Bài 6.Tìm x, biết:

a) $\sqrt{x}=\frac{1}{2};$

b) $\sqrt[3]{x-10}=5;$

c) $5\sqrt{8-4\text{x}}-2\sqrt{32-16\text{x}}=10.$

Hướng dẫn giải

a) Điều kiện xác định x ≥ 0.

$\sqrt{x}=\frac{1}{2}$

${\left(\sqrt{x}\right)}^2={\left(\frac{1}{2}\right)}^2$

$x=\frac{1}{4}$ (thỏa mãn điều kiện).

Vậy $x=\frac{1}{4}$

b) $\sqrt[3]{x-10}=5$

${\left(\sqrt[3]{x-10}\right)}^3=5^3$

x – 10 = 125

x = 135

Vậy x = 135.

c) Điều kiện xác định x ≤ 2.

$5\sqrt{8-4\text{x}}-2\sqrt{32-16\text{x}}=10$.

$5\sqrt{4\left(2-\text{x}\right)}-2\sqrt{16\left(2-\text{x}\right)}=10$

$10\sqrt{\left(2-\text{x}\right)}-8\sqrt{\left(2-\text{x}\right)}=10$

$2\sqrt{\left(2-\text{x}\right)}=10$

$\sqrt{\left(2-\text{x}\right)}=5$

2 – x = 25

x = –23 (thỏa mãn điều kiện).

Vậy x = –23.

Bài 7.Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 360m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m).

a) Viết biểu thức biểu thị khoảng cách BC từ trạm phát sóng đến đầu tàu.

b) Tính khoảng cách trên khi x = 480, x = 900 (làm tròn kết quả đến hàng đơn vị của mét).

Hướng dẫn giải

a) Áp dụng định lí Pythagorecho tam giác ABC vuông tại A, ta có:

BC² = AC² + AB²

Suy ra: $BC=\sqrt{A{C}^2+A{B}^2}=\sqrt{x^2+{360}^2}=\sqrt{x^2+129600}$ (m).

Vậy biểu thức biểu thị khoảng cách từ trạm phát sóng đến đầu tàu là $BC=\sqrt{x^2+129600}$ (m).

b) Khi x = 480, thay vào biểu thức $BC=\sqrt{x^2+129600}$ thì khoảng cách trên bằng:

$\sqrt{{480}^2+129600}=\sqrt{230400+129600}=\sqrt{360000}=600$ (m).

Khi x = 900, thay vào biểu thức $BC=\sqrt{x^2+129600}$ thì khoảng cách trên bằng:

$\sqrt{{900}^2+129600}=\sqrt{810000+129600}=\sqrt{939600}\approx 969$ (m).

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 2: Một số phép tính về căn bậc hai của số thực

Lý thuyết Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

Lý thuyết Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Lý thuyết Bài 1: Tỉ số lượng giác của góc nhọn

Lý thuyết Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Lý thuyết Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn